学习总结

• 本次学习任务：理解泛化误差分解的过程，掌握bagging的性质，掌握四种集成模式的工作流程。实现stacking和blending。集成学习讨论的是如何将基分类器集成起来；集成学习一般分为3个步骤：找到误差互相独立的基分类器；训练基分类器；合并基分类器的结果。

• 偏差：由于分类器的表达能力有限导致的系统性错误，表现在训练误差不收敛；
  方差：分类器对于样本分布过于敏感，导致在训练样本数较少时，产生过拟合。

• 基分类器的错误 = 偏差 + 方差
  Boosting通过逐步聚集基分类器分错的样本，减少集成分类器的偏差；Bagging通过分而治之的策略，通过对训练样本多次采用，综合决策多个训练出来的模型，来减少集成分类器的方差。
• stacking严格来说并不是一种算法，而是精美而又复杂的，对模型集成的一种策略。Stacking集成算法可以理解为一个两层的集成，第一层含有多个基础分类器，把预测的结果(元特征)提供给第二层， 而第二层的分类器通常是逻辑回归，他把一层分类器的结果当做特征做拟合输出预测结果。
• 挖个坑，kaggle的一文Introduction to Ensembling/Stacking in Python要补。

一、集成的原因

我们在有限数据上训练模型，再用模型去预测新的数据，并期望在新数据上得到较低的预测损失，这里的预测损失可以指分类问题的错判率或回归问题的均方误差等各类评价指标。
对于实际问题中的数据，可以认为它总是由某一个分布$p$生成得到的，不妨设训练集合上有限的$n$个样本满足：

$${\text{X}}_1,{\text{X}}_2,...,{\text{X}}_n\sim p(\text{X})$$

而这些样本对应的标签是通过真实模型$f$和噪声${ϵ}_1,{ϵ}_2,...,{ϵ}_n$得到的，即

y i = f ( X i ) + ϵ i , i ∈ { 1 , 2 , . . . , n } y_i = f(\textbf{X}_i)+\epsilon_i,i\in\{1,2,...,n\} yi​=f(Xi​)+ϵi​,i∈{1,2,...,n}

其中，假设噪声均值为$0$且方差为${\sigma }^2$。此时，我们得到了一个完整的训练集 D = { ( X 1 , y 1 ) , ( X 2 , y 2 ) , . . . , ( X n , y n ) } D=\{(\textbf{X}_1,y_1), (\textbf{X}_2,y_2),...,(\textbf{X}_n,y_n)\} D={(X1​,y1​),(X2​,y2​),...,(Xn​,yn​)}

对于新来的样本$\tilde{\text{X}}\sim p(\text{X})$，我们需要对其标签$$y=f({\text{X}}_i)+{ϵ}_i$$进行预测，假设当前处理的是回归问题，应学习一个模型$\hat{f}$使得平方损失$$(y-\hat{f}(\tilde{\text{X}}){)}^2$$尽可能地小。

注意：$\hat{f}$不仅是$\tilde{\text{X}}$的函数，由于它是从训练集上得到的，而训练集是从总体分布随机生成的有限分布，因此平方损失实际应记为为$$(y-{\hat{f}}_D(\tilde{\text{X}}){)}^2$$

由于$D$是一个随机变量，故本质上优化的应当是$$L={\mathbb{E}}_D(y-{\hat{f}}_D(\tilde{\text{X}}){)}^2$$

这表示我们希望在按照给定分布任意生成的数据集上训练出的模型都能够有较好的预测能力，即模型具有良好的泛化性。

为了进一步研究$L$，我们把模型（基于不同数据集对新样本特征）的平均预测值信息$${\mathbb{E}}_D[{\hat{f}}_D(\tilde{\text{X}})]$$添加到$L$中，此时存在如下分解：

$$\begin{array}{rl}L(\hat{f})& ={\mathbb{E}}_D(y-{\hat{f}}_D{)}^2\\ & ={\mathbb{E}}_D(f+ϵ-{\hat{f}}_D+{\mathbb{E}}_D[{\hat{f}}_D]-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])+({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)+ϵ{]}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2]+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\mathbb{E}}_D[{ϵ}^2]\\ & =[f-{\mathbb{E}}_D[{\hat{f}}_D]{]}^2+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\sigma }^2\end{array}$$

【练习】左式第四个等号为何成立？
交叉项约去了。

上式中可见，预测数据产生的平均损失来自于三项。其中：

• 第一项为数据真实值与模型平均预测值的偏差，偏差越小则代表模型的学习能力越强，能够较好地拟合数据，
• 第二项为模型预测值的方差（注意$\hat{f}$应视作随机变量$D$的函数，故$\hat{f}$是随机变量），方差越小则代表模型的抗干扰能力越强，不易因为数据的扰动而对预测结果造成大幅抖动，
• 第三项为数据中的原始噪声，它是不可能通过优化模型来降解的。这种分解为我们设计模型提供了指导，即可以通过减小模型的偏差来降低测试数据的损失，也可以通过减少模型的预测方差来降低损失。

【练习】有人说Bias-Variance Tradeoff就是指“一个模型要么具有大的偏差，要么具有大的方差”，你认为这种说法对吗？你能否对“偏差-方差权衡”现象做出更准确的表述？

对于一个具体的学习问题，过于简单的学习器虽然抗干扰能力强，但由于不能充分拟合数据却会造成大的偏差，从而导致总的期望损失较高；类似地，过于复杂的学习器虽然其拟合能力很强，但由于学习了多余的局部信息，因此抗干扰能力较弱造成较大的方差，从而导致总的期望损失较高。上述联系由下图表达。

既然对单个学习器的偏差和方差的降解存在难度，那我们可以使用多个学习器进行结果的集成以进一步减小损失：

• Boosting通过逐步聚集基分类器分错的样本，减少集成分类器的偏差；
• Bagging通过分而治之的策略，通过对训练样本多次采用，综合决策多个训练出来的模型，来减少集成分类器的方差。

二、Bagging与Boosting

2.1 Bagging（集体投票决策）

Bagging是一种并行集成方法（各基分类器之间无强依赖，可以并行训练），其全称是$\text{b}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{p}\text{ag}\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{t}\text{ing}$，即基于bootstrap抽样的聚合算法。随机森林算法就是一种基于bagging的模型，在最终决策时，每个个体单独做出判断后再进行投票作集体决策。

（1）Bootstrap抽样

Bootstrap抽样：指从样本集合中进行有放回的抽样，假设数据集的样本容量为$n$且基学习器的个数为$M$，对于每个基学习器我们可以进行有放回地抽取$n$个样本，从而生成了$M$组新的数据集，每个基学习器分别在这些数据集上进行训练，再将最终的结果汇总输出。

那这样的抽样方法有什么好处呢？
我们已经知道数据集是从总体分布$p(\text{X})$中抽样得到的，此时数据集构成了样本的经验分布$\tilde{p}(\text{X})$，由于采用了有放回抽样，因此$M$个数据集中的每一组新样本都来自于经验分布$\tilde{p}(\text{X})$。同时由大数定律知，当样本量$n\to \infty$时，经验分布$\tilde{p}(\text{X})$收敛到总体分布$p(\text{X})$，因此大样本下的新数据集近似地抽样自总体分布$p(\text{X})$。

假设我们处理的是回归任务，并且每个基学习器输出值$y^{(i)}$的方差为${\sigma }^2$，基学习器两两之间的相关系数为$\rho$，则可以计算集成模型输出的方差为

$$\begin{array}{rl}Var(\hat{y})& =Var(\frac{{\sum }_{i=1}^M{y}^{(i)}}{M})\\ & =\frac{1}{M^2}[\sum _{i=1}^{M}Var(y^{(i)})+\sum _{i\ne j}Cov(y^{(i)},y^{(j)})]\\ & =\frac{1}{M^2}[M{\sigma }^2+M(M-1)\rho {\sigma }^2]\\ & =\rho {\sigma }^2+(1-\rho )\frac{{\sigma }^2}{M}\end{array}$$

从上式的结果来看，当基模型之间的相关系数为1时方差不变，这相当于模型之间的输出完全一致，必然不可能带来方差的降低。

bootstrap的放回抽样特性保证了模型两两之间很可能有一些样本不会同时包含，这使模型的相关系数得以降低，而集成的方差随着模型相关性的降低而减小，如果想要进一步减少模型之间的相关性，那么就需要对基学习器进行进一步的设计。

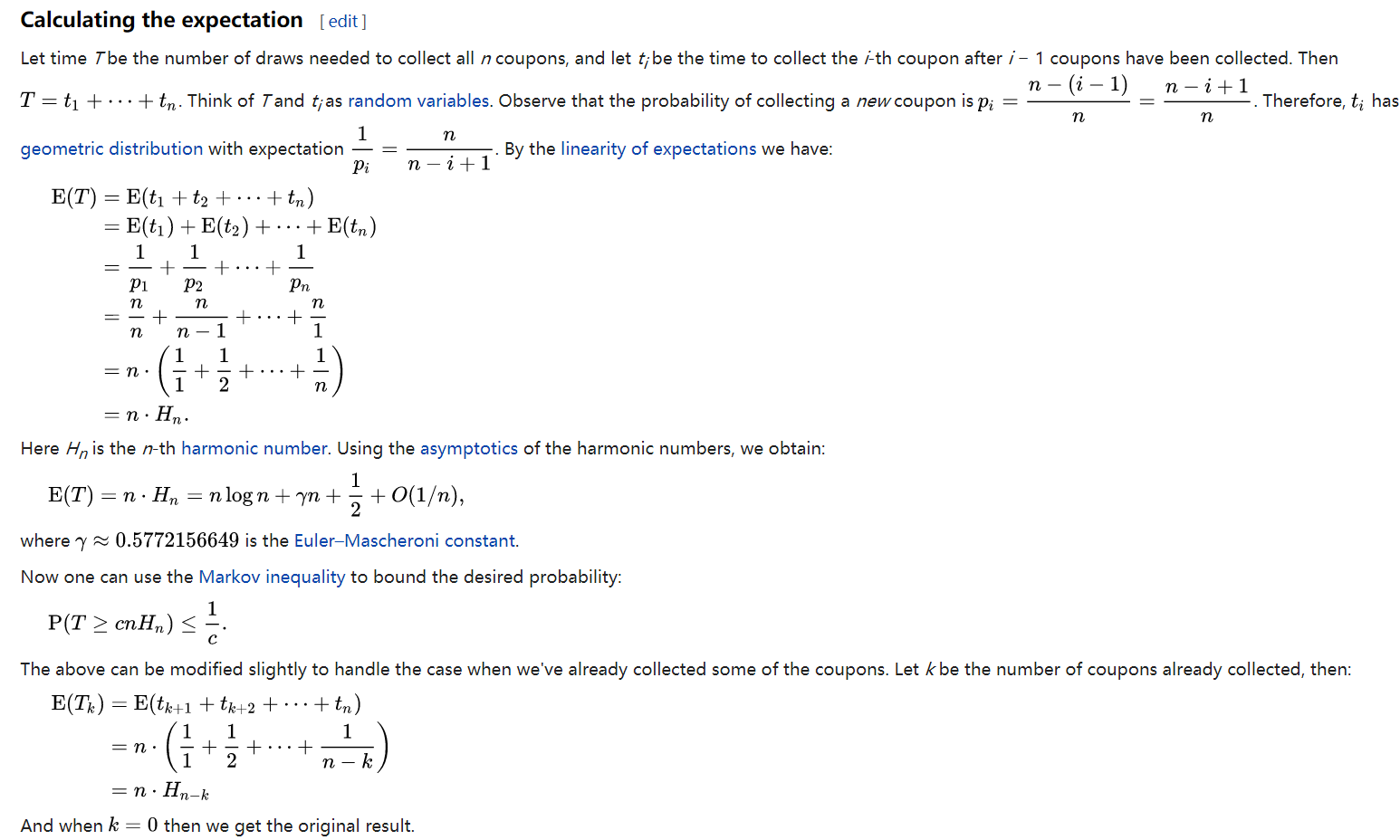
【练习】假设总体有$100$个样本，每轮利用bootstrap抽样从总体中得到$10$个样本（即可能重复），请求出所有样本都被至少抽出过一次的期望轮数。（通过本文介绍的方法，我们还能得到轮数方差的bound）

（2）bootstrap造成的数据集差异

为了更具体地了解bootstrap造成的数据集差异，我们往往对两个量是非常关心的，它们分别是单个样本的入选概率和入选（非重复）样本的期望个数。我们首先计算第一个量：对于样本容量为$n$的原数据集，抽到某一个给定样本的概率是$\frac{1}{n}$，进行$n$次bootstrap采样但却没有选入该样本的概率为$(1-\frac{1}{n}{)}^n$，从而该样本入选数据集的概率为$$1-(1-\frac{1}{n}{)}^n$$，当$n\to \infty$时的概率为$1-e^{-1}$。对于第二个量而言，记样本$i$在$n$次抽样中至少有一次入选这一事件为$A_i$，那么非重复样本的个数为 ∑ i = 1 n 1 { A i } \sum_{i=1}^n\mathbb{1}_{\{A_i\}} i=1∑n​1{Ai​}​ 从而期望个数为

E ∑ i = 1 n 1 { A i } = ∑ i = 1 n E 1 { A i } = ∑ i = 1 n P ( A i ) = ∑ i = 1 n 1 − ( 1 − 1 n ) n = n [ 1 − ( 1 − 1 n ) n ] \begin{aligned} \mathbb{E}\sum_{i=1}^n\mathbb{1}_{\{A_i\}} &= \sum_{i=1}^n\mathbb{E}\mathbb{1}_{\{A_i\}} \\ &= \sum_{i=1}^nP(A_i)\\ &= \sum_{i=1}^n 1-(1-\frac{1}{n})^n\\ &= n[1-(1-\frac{1}{n})^n] \end{aligned} Ei=1∑n​1{Ai​}​​=i=1∑n​E1{Ai​}​=i=1∑n​P(Ai​)=i=1∑n​1−(1−n1​)n=n[1−(1−n1​)n]​

若$n\to \infty$时，入选样本占原数据集的期望比例为
lim ⁡ n → ∞ E ∑ i = 1 n 1 { A i } n = lim ⁡ n → ∞ [ 1 − ( 1 − 1 n ) n ] \displaystyle \lim_{n\to \infty}\frac{\mathbb{E}\sum_{i=1}^n\mathbb{1}_{\{A_i\}}}{n}=\lim_{n\to\infty} [1-(1-\frac{1}{n})^n] n→∞lim​nE∑i=1n​1{Ai​}​​=n→∞lim​[1−(1−n1​)n]即$1-e^{-1}$。

2.2 Boosting

Boosting是一种串行集成方法（迭代式学习），各个基分类器之间有依赖。每层在训练时，对前一层基分类器分错的样本，给予更高的权重。

假设第$i$个基模型的输出是$${\hat{f}}^{(i)}(\mathbf{X})$$ 则总体模型的输出为${\sum }_{i=1}^M{\alpha }_i{\hat{f}}^{(i)}(\tilde{X})$。boosting算法在拟合第$T$个学习器时，已经获得了前$T-1$个学习器的集成输出
$$\sum _{i=1}^{T-1}{\alpha }_i{\hat{f}}^{(i)}(\mathbf{X})$$

对于损失函数$L(y,\hat{y})$，当前轮需要优化的目标即为使得
$$L(y,{\alpha }_T{\hat{f}}^{(T)}(\mathbf{X})+\sum _{i=1}^{T-1}{\alpha }_i{\hat{f}}^{(i)}(\mathbf{X}))$$

最小化。注意：当前轮所有需要优化的参数一般而言都会蕴藏在${\alpha }_T{\hat{f}}^{(T)}$这一项中，不同的模型会对$${\alpha }_T{\hat{f}}^{(T)}$$提出的不同假设。此外，由于优化损失在经验分布与总体分布相差不多的时候等价于优化了模型的偏差，因此多个模型集成后相较于单个模型的预测能够使得偏差降低。

Boosting的过程很类似于人类学习的过程，我们学习新知识的过 程往往是迭代式的，第一遍学习的时候，我们会记住一部分知识，但往往也会犯 一些错误，对于这些错误，我们的印象会很深。第二遍学习的时候，就会针对犯 过错误的知识加强学习，以减少类似的错误发生。不断循环往复，直到犯错误的 次数减少到很低的程度。

三、stacking与blending

Stacking流程比较复杂因为涉及到交叉验证的过程，其流程与Blending类似，具体如下：

• 将数据划分为训练集和测试集(test_set)，对训练集进行划分为K个大小相似的集合，取其中一份作为验证集val_set,其余的为训练集train_set；
• 创建第一层的多个模型，这些模型可以使同质的也可以是异质的；
• 对于每一个模型来说，train_set和val_set是不一样的，如下图所示；然后利用各自的train_set训练各自的模型，训练好的模型对各自的val_set和test_set进行预测，得到val_predict和test_predict；
• 创建第二层的模型，将每个模型对应的val_predict拼接起来作为第二层的训练集，将所有模型的test_predict取平均值作为第二层的测试集；用训练好的第二层模型对第二层的测试集进行预测，得到的结果即为整个测试集的结果

stacking 网上有两种解释：

• 一种是单个模型进行5次交叉验证得到一个结果，然后对每个模型都进行相同的操作，此时训练集的维度为(样本数目 x 模型数目)；
• 另一种是每个模型对数据的每一折输出一个结果，然后把每一折的结果拼接起来，此时的训练集维度(样本数目 x 1)。

3.1 stacking

stacking本质上也属于并行集成方法，但其并不通过抽样来构造数据集进行基模型训练，而是采用$K$折交叉验证。

假设数据集大小为$N$，测试集大小为$M$，我们先将数据集均匀地分为$K$份。对于第$m$个基模型，我们取$K$折数据集中的1折为验证集，在剩下的$K-1$折为训练集，这样依次取遍$K$份验证数据就可以分别训练得到$K$个模型以及$K$份验证集上的相应预测结果，这些预测结果恰好能够拼接起来作为基模型在训练集上的学习特征$F_m^{train}$。

同时，我们还需要利用这$K$个模型对测试集进行预测，并将结果进行平均作为该基模型的输出$F_m^{test}$。对每个基模型进行上述操作后，我们就能得到对应的训练集特征$$F_1^{train},...,F_M^{train}$$以及测试集特征$$F_1^{test},...,F_M^{test}$$

此时，我们使用一个最终模型$f$，以$$F_1^{train},...,F_M^{train}$$为特征，以训练集的样本标签为目标进行训练。在$f$拟合完成后，以$$F_1^{test},...,F_M^{test}$$为模型输入，得到的输出结果作为整个集成模型的输出。

【练习】对于stacking和blending集成而言，若$m$个基模型使用$k$折交叉验证，此时分别需要进行几次训练和几次预测？
训练是m×k+1次，测试是2×m×k+1次。

整个stacking的流程如下图所示，我们在3种基学习器使用4折交叉验证，因此图中的左侧部分需要12次训练，右侧的浅红色和深红色表示的是同一个最终模型，使用不同颜色是为了主要区分训练前和训练后的状态。

注意：整个集成模型一共包含了25次（即2×12+1）预测过程，即每个基模型对各折数据的预测、每个基模型对测试集数据的预测以及最终模型的1次预测。

3.2 blending

blending集成与stacking过程类似，它的优势是模型的训练次数更少，但其缺陷在于不能使用全部的训练数据，相较于使用交叉验证的stacking稳健性较差。blending在数据集上按照一定比例划分出训练集和验证集，每个基模型在训练集上进行训练，并记验证集上的预测结果为$$F_1^{train},...,F_M^{train}$$

同时，我们还需要用这些基模型对测试集进行预测，其结果为$$F_1^{test},...,F_M^{test}$$

最后的流程与stacking一致，即以用$$F_1^{train},...,F_M^{train}$$和验证集的样本标签来训练最终模型，并将$$F_1^{test},...,F_M^{test}$$输入训练后的最终模型以得到模型的总体预测结果。假设仍然使用3种基学习器，由于无须交叉验证，此时只需要4次训练（含最终模型）和7次预测过程。

四、作业

5.1 什么是偏差和方差分解？偏差是谁的偏差？此处的方差又是指什么？

把模型（基于不同数据集对新样本特征）的平均预测值信息$${\mathbb{E}}_D[{\hat{f}}_D(\tilde{\text{X}})]$$添加到$L$中，此时存在如下分解：

$$\begin{array}{rl}L(\hat{f})& ={\mathbb{E}}_D(y-{\hat{f}}_D{)}^2\\ & ={\mathbb{E}}_D(f+ϵ-{\hat{f}}_D+{\mathbb{E}}_D[{\hat{f}}_D]-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])+({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)+ϵ{]}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2]+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\mathbb{E}}_D[{ϵ}^2]\\ & =[f-{\mathbb{E}}_D[{\hat{f}}_D]{]}^2+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\sigma }^2\end{array}$$

• 偏差：由于分类器的表达能力有限导致的系统性错误，表现在训练误差不收敛；偏差一般是由于我们对学习算法做了错误的假设所导致的，比如真实模型是某个二次函数，但我们假设模型是一次函数。
• 方差：分类器对于样本分布过于敏感，导致在训练样本数较少时，产生过拟合。方差一般是由于模型的复杂度相对于训练样本数m过高导致的，比如一共有100个训练样本，而我们假设模型是阶数大于200的多项式函数。

首先 Error = Bias + VarianceError反映的是整个模型的准确度，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。

5.2 相较于使用单个模型，bagging和boosting方法有何优势？

基分类器的错误 = 偏差 + 方差

• Boosting通过逐步聚集基分类器分错的样本，减少集成分类器的偏差；训练好一个弱分类器后，计算其错误或残差，作为下一个分类器的输入——该过程在不断减小损失函数，使模型不断逼近“靶心”。
• Bagging通过分而治之的策略，通过对训练样本多次采用，综合决策多个训练出来的模型，来减少集成分类器的方差。 有点不严谨地说，对n个独立不相关的模型的预测结果取平均， 方差是原来单个模型的1/n。

5.3 请叙述stacking的集成流程，并指出blending方法和它的区别。

Stacking流程比较复杂因为涉及到交叉验证的过程，其流程与Blending类似，具体如下：

• 将数据划分为训练集和测试集(test_set)，对训练集进行划分为K个大小相似的集合，取其中一份作为验证集val_set,其余的为训练集train_set；
• 创建第一层的多个模型，这些模型可以使同质的也可以是异质的；
• 对于每一个模型来说，train_set和val_set是不一样的，如下图所示；然后利用各自的train_set训练各自的模型，训练好的模型对各自的val_set和test_set进行预测，得到val_predict和test_predict；
• 创建第二层的模型，将每个模型对应的val_predict拼接起来作为第二层的训练集，将所有模型的test_predict取平均值作为第二层的测试集；用训练好的第二层模型对第二层的测试集进行预测，得到的结果即为整个测试集的结果

5.4 stacking代码实践

# -*- coding: utf-8 -*-
"""
Created on Wed Oct 20 19:35:23 2021

@author: 86493
"""
from sklearn.model_selection import KFold
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.svm import LinearSVR

import numpy as np
import pandas as pd

# 模型融合中使用到的各个单模型
m1 = KNeighborsRegressor()
m2 = DecisionTreeRegressor()
m3 = LinearRegression()

models = [m1, m2, m3]
final_model = LinearSVR()

# m为model基模型的数量，此处为3
k, m = 4, len(models)

if __name__ == "__main__":
    # 模拟回归数据集
    # 模拟出来的训练集
    X, y = make_regression(
        n_samples = 1000,
        n_features = 8,
        n_informative = 4,
        random_state = 0
    )
    # 模拟出来的测试集
    # 测试集的label得不到，所以用下划线了
    final_X, _ = make_regression(
        n_samples = 500,
        n_features = 8,
        n_informative = 4, 
        random_state = 0
    )
    
    final_train = pd.DataFrame(np.zeros((X.shape[0], m)))
    final_test = pd.DataFrame(np.zeros((final_X.shape[0], m)))
    
    # 4折stacking
    kf = KFold(n_splits = k)
    # 第一层循环控制基模型的数目
    for model_id in range(m):
        model = models[model_id]
        # 第二层循环控制的是交叉验证的次数
        for train_index, test_index in kf.split(X):
            X_train, X_test = X[train_index], X[test_index]
            y_train, y_test = y[train_index], y[test_index]
            model.fit(X_train, y_train)
            final_train.iloc[test_index, model_id] += model.predict(X_test)
            final_test.iloc[:, model_id] += model.predict(final_X)
        final_test.iloc[:, model_id] /= m
    
    final_model.fit(final_train, y)
    res = final_model.predict(final_test)
    # print("res:\n", res)

5.5 基分类器用树型模型的原因

集成学习一般三部曲的第一步是【找到误差互相独立的基分类器】，事实上，任何 分类模型都可以作为基分类器，但树形模型由于结构简单且较易产生随机性所以比较常用。具体的3点原因：

• 决策树可以较为方便地将样本的权重整合到训练过程中，而不需要使用 过采样的方法来调整样本权重。
• 决策树的表达能力和泛化能力，可以通过调节树的层数来做折中。
• 数据样本的扰动对于决策树的影响较大，因此不同子样本集合生成的决 策树基分类器随机性较大，这样的“不稳定学习器”更适合作为基分类器。此外， 在决策树节点分裂的时候，随机地选择一个特征子集，从中找出最优分裂属性， 很好地引入了随机性。 除了决策树外，神经网络模型也适合作为基分类器，主要由于神经网络模型 也比较“不稳定”，而且还可以通过调整神经元数量、连接方式、网络层数、初始 权值等方式引入随机性。

Reference

（1）https://datawhalechina.github.io/machine-learning-toy-code/index.html
（2）详解stacking过程
（3）图解Blending&Stacking
（4）Stacking Ensemble Machine Learning With Python
（6）StackingClassifier
（7）https://zh.wikipedia.org/zh-cn/%E9%9B%86%E6%88%90%E5%AD%A6%E4%B9%A0
（8）datawhale notebook
（9）集成学习（ensemble learning）
（10）https://github.com/InsaneLife/MyPicture/blob/master/ensemble_stacking.py
（11）某同学笔记
（12）Stacking方法详解