参考资料：R语言实战【第2版】

        支持向量机（SVM）是一类可用于分类和回归的有监督机器学习模型。其流行归功于两个方面：一方面，他们可输出较准确的预测结果；另一方面，模型基于较优雅的数学理论。这里主要介绍支持向量机在二元分类问题中的应用。

        SVM旨在多为空间中找到一个能够将全部样本单元分成两类的最优（超）平面，这一平面应使两类中距离最近的点的间距（margin）尽量大，在间距边界上的点被称为支持向量（support vector，它们决定间距），分割的超平面位于间距的中间。

        对于一个N维空间（即N个变量）来说，最优超平面(即线性决策面，linear decision surface)为N-1维。当变量数为2时，曲面是一条直线；当变量数为3时，曲面是一个平面；当变量数为10时，曲面就是一个九维的超平面。

        如下图的二维问题：圆圈和三角形分别代表两个不同类别，间距即两根虚线间的距离。虚线上的点（实心圆圈和实心三角形）即支持向量。在二维问题中，最优超平面即间距中黑色实线。在这个理想化案例中，这两类样本单元是线性可分的，即黑色实线可以无误差地准确区分两类。

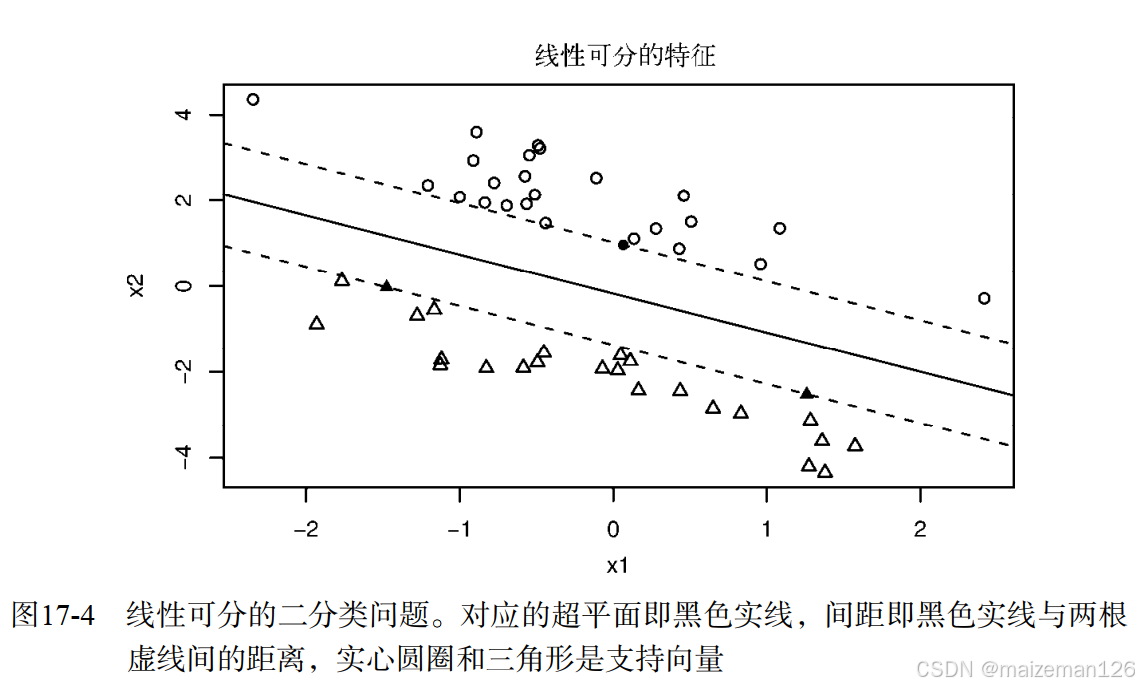
        最优超平面可由一个二次规划问题解得。二次规划问题限制一侧样本点的输出值为+1，另一侧的输出值为-1，在此基础上最优化间距。若样本点“几乎”可分（即并非所有样本点都集中在一侧），则在最优化中加入惩罚项以容许一定误差，从而生成“软”间隔。

        有可能数据本身就是非线性的，如下图中就不存在完全分开圆圈和三角形的线。在这种情况下，SVM通过核函数将数据投影到高纬度，使其在高维线性可分。

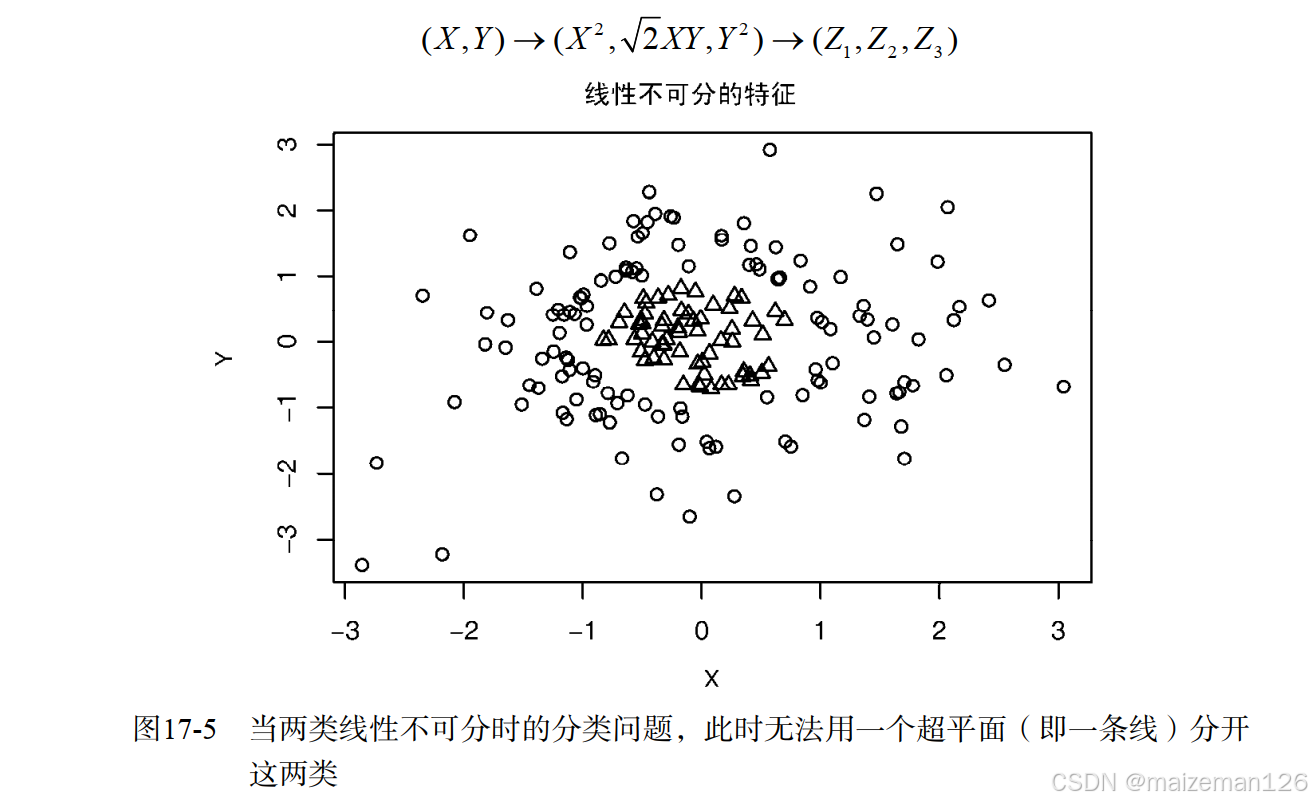
        SVM的数据解释化比较复杂，这里不讨论。AVM可以通过R中的kernlab包中的ksvm()函数和e1071包中的svm()函数实现。ksvm()功能更强大，但svm()相对简单。下面用svm()函数进行演示：

1、数据准备

# 确保已安装相关分析包
pkgs<-c("rpart","rpart.plot","party",
        "randomForest","e1071")
install.packages("randomForest")
install.packages("e1071")
install.packages(pkgs,depend=TRUE)
# 数据准备
loc<-"http://archive.ics.uci.edu/ml/machine-learning-databases/"
ds<-"breast-cancer-wisconsin/breast-cancer-wisconsin.data"
url<-paste(loc,ds,sep="")
breast<-read.table(url,sep=",",
                  header=FALSE,
                  na.strings="?")
names(breast)<-c("ID","clumpThickness","sizeUniformity",
                 "shapeUniformity","maginalAdhesion",
                 "singleEpitheliaCellSize","bareNucei",
                 "blandChromatin","normalNucleoli","mitosis","class")
df<-breast[-1]
df$class<-factor(df$class,levels=c(2,4),
                 labels=c("benign","malignant"))
set.seed(1234) # 设置随机种子用于复现结果
train<-sample(nrow(df),0.7*nrow(df))
df.train<-df[train,] # 训练集
df.validata<-df[-train,] # 验证集
table(df.train$class)
table(df.validata$class)

2、SVM分析

# 加载e1071包
library(e1071)
# 设置随机种子
set.seed(1234)
# SVM分析
fit.svm<-svm(class~.,data=df.train)
# 查看结果
fit.svm
# 数据验证
svm.pred<-predict(fit.svm,na.omit(df.validata))
svm.perf<-table(na.omit(df.validata)$class,
                svm.pred,dnn=c("Actual","Predicted"))
svm.perf

        由于方差较大的预测变量通常对SVM的生成影响较大，svm()函数默认在生成模型前对每个变量标准化，使其均值为0、标准差为1。另外，SVM在预测新样本单元时不允许有缺失值的出现。

3、选择调和参数

        svm()函数通过默认通过径向基函数（Radial Basis Function, RBF）将样本单元投射到高维空间。一般来说RBF核是一个比较好的选择，因为它是一种非线性投影，可以应对类别标签与预测变量间的非线性关系。

        在用带RBF核的SVM拟合样本时，两个参数可能影响最终结果：gamma和成本（cost）。gamma是核函数的参数，控制分割超平面的形状。gamma越大，通常导致支持向量越多。我们也可将gamma看作控制训练样本“到达范围”的参数，即gamma越大意味着训练样到达范围越广，而越小则意味着到达范围越窄。gamma必须大于0.

        成本参数代表犯错的成本。一个较大的成本意味着模型对误差的惩罚更大，从而将生成一个更复杂的分类边界，对应的训练集中的误差也会更小，但也意味着可能存在过拟合问题，即对新样本单元的预测误差可能很大。较小的成本意味着分类边界更平滑，但可能会导致欠拟合。与gamma一样，成本参数也恒为正。

        svm()函数默认设置gamma为预测变量个数的倒数，成为参数为1。不过gamma与成本参数的不同组合可能生成更有效的模型。在建模时，我们可以尝试变动参数值建立不同的模型，但利用格点搜索法可能更有效。可以通过tune.svm()对每个参数设置一个候选范围，tune.svm()函数对每一个参数组合生成一个SVM模型，并输出在每一个参数组合上的表现。如下：

# 设置随机种子
set.seed(1234)
# 变换参数并输出最优模型
tuned<-tune.svm(class~.,data=df.train,
                gamma=10^(-6:1),
                cost=10^(-10:10))
tuned
# 利用最优参数进行模型设置
fit.svm<-svm(class~.,data=df.train,
             gamma=0.01,
             cost=1)
# 用验证数据集对模型进行验证
svm.pred<-predict(fit.svm,na.omit(df.validata))
svm.perf<-table(na.omit(df.validata)$class,svm.pred,
                dnn=c("Actual","Predicted"))
svm.perf

        上述代码，首先对不同的gamma和cost参数拟合了一个带RBF的SVM的模型。我们一共尝试了8个不同的gamma(从0.000001到10)以及21个cost参数。总体来说，我们工拟合和8*21个模型，并比较了其结果【见下图】。训练集中10折交叉验证误差最小的模型所对应的参数为gamma=0.1，cost=1。

        基于上述最优参数组合，我们对全部训练样本拟合出新的SVM模型，然后利用这一模型对验证数据集的样本单元进行预测，并给出混淆矩阵。预测结果优于未进行参数设置时的预测结果。一般来说，为SVM模型选取调和参数通常可以得到更好结果。

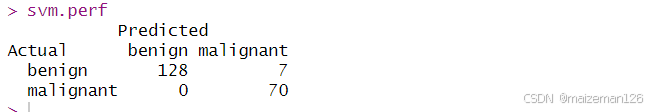
        SVM可用应用于变量数远多于样本单元数的问题，而这类问题在生物医药行业很常见，因为在DNA微序列的基因表示中，变量通常比可用样本量的个数高1~2个量级。

        与随机森林类似，SVM的一大缺点是分类准则比较难以理解和表述。SVM在本质上说是一个黑盒子。另外，SVM在对大量样本建模时不如随机森林，但只要建立一个成功的模型，在对新样本分类时就没有问题了。