本系列博客基于温州大学黄海广博士的机器学习课程的笔记，小伙伴们想更详细学习黄博士课程请移步到黄博士的Github、或者机器学习初学者公众号，现在在中国慕课也是可以学习的，内容包括机器学习、深度学习及Python编程，matplotlib、numpy、pandas、sklearn等，资料很详细，要系统学习请移步哦！笔者的博客只是笔记，内容不会十分详细，甚至会有些少错误！

1.几个基本概念

# 回归概念：
# 监督学习分为：回归(Regression)、分类(Classification)

# 1.回归(Regression、Prediction)--标签是连续的；
# a.预测上海浦东的房价；
# b.预测未来股票市场走向；

# 2.分类(Classification)--标签是离散的；
# a.身高170cm，体重60kg的男人穿什么尺码的牛仔裤；
# b.根据肿瘤的体积、患者的年龄来判断肿瘤是良性还是恶性；

# 线性回归(Linear Regression)：通过属性的线性组合进行预测的线性模型；
# 目的：找到一条直线或一个平面或更高维的超平面，使得预测值与真实值之间的误差最小化；

2.线性回归

2.1 一些相关符号约定

• $m$：训练集中样本的数量；
• $n$：特征的数量；
• $x$：特征/输入变量；
• $y$：目标变量/输出变量；
• $(x,y)$：训练集中的样本；
• $(x^{(i)},y^{(i)})$：第i个观测样本；
• $h$：学习算法的解决方案或函数，称为假设(hypothesis)；
• $\hat{y}=h(x)$：预测的值;
• $x^{(i)}$：特征矩阵中的第$i$行，一个向量；
• $x_j^{(i)}$：特征矩阵中的第$i$行的第$j$个特征；

2. 2 三个函数

• 损失函数(Loss Function)：度量单样本预测的错误程度，损失函数值越小，模型越好；常用的损失函数：0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等；
• 代价函数(Cost Function)：度量全部样本集的平均误差；常用的代价函数：均方误差、均方根误差、平均绝对误差等；
• 目标函数(Object Function)：代价函数和正则化函数，最终要优化的函数；

2.3 回归算法流程(最小二乘法)

1. $x、y关系$：$$h(x)={\omega }_0+{\omega }_1{x}_1+{\omega }_2{x}_2+\cdots +{\omega }_n{x}_n$$

2. 设$x_0=1$，则有$$h(x)={\omega }_0{x}_0+{\omega }_1{x}_1+{\omega }_2{x}_2+\cdots +{\omega }_n{x}_n={\omega }^{T}X$$

3. 损失函数采用平方和损失：$$l(x^{(i)})=\frac{1}{2}(h(x^{(i)})-y^{(i)}{)}^2$$

4. 找到一组$$\omega ({\omega }_0,{\omega }_1,{\omega }_2,\dots ,{\omega }_n)$$使得$$J(\omega )=\frac{1}{2}\sum _{i=1}^m(h(x^{(i)})-y^{(i)}{)}^2最小$$

5. 要找到一组$$\omega ({\omega }_0,{\omega }_1,{\omega }_2,\dots ,{\omega }_n)$$使得$$J(\omega )=\frac{1}{2}\sum _{i=1}^m(h(x^{(i)})-y^{(i)}{)}^2最小$$即最小化：$$\frac{\partial J(\omega )}{\partial \omega }$$

6. 将向量表达式转换为矩阵表达式，有：$$J(\omega )=\frac{1}{2}(X\omega -Y{)}^2$$
   $$\begin{gathered} 其中： \\ X：m行n+1列的矩阵(m为样本个数，n为特征个数)； \\ \omega ：n+1行1列的矩阵(包含{\omega }_0)； \\ Y：m行1列矩阵； \end{gathered}$$

7. 由上可得：$$J(\omega )=\frac{1}{2}(X\omega -Y{)}^2=\frac{1}{2}(X\omega -Y{)}^T(X\omega -Y)$$
   其中：
   $$X=\left[\begin{array}{ccccc}1& x_1^{(1)}& x_2^{(1)}& \dots & x_n^{(1)}\\ 1& x_1^{(2)}& x_2^{(2)}& \dots & x_n^{(2)}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& x_1^{(m)}& x_2^{(m)}& \dots & x_n^{(m)}\end{array}\right]，Y=\left[\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ ⋮\\ y^{(m)}\end{array}\right]$$

8. 对$J(\omega )$求偏导：
   $$\begin{array}{rl}\frac{\partial J(\omega )}{\partial \omega }& =\frac{1}{2}\frac{\partial }{\partial \omega }(X\omega -Y{)}^T(X\omega -Y)\\ & =\frac{1}{2}\frac{\partial }{\partial \omega }({\omega }^T{X}^{T}X\omega -Y^{T}X\omega -{\omega }^T{X}^{T}Y+Y^{T}Y)\\ & =\frac{1}{2}\frac{\partial }{\partial \omega }({\omega }^T{X}^{T}X\omega -2{\omega }^T{X}^{T}Y+Y^{T}Y)\\ & =\frac{1}{2}(2X^{T}X\omega -2X^{T}Y+0)\\ & =X^{T}X\omega -X^{T}Y\end{array}$$

9. 令$$\frac{\partial J(\omega )}{\partial \omega }=0$$则有：$$\omega =(X^{T}X{)}^{-1}{X}^{T}Y$$

3.梯度下降

梯度下降的三种形式：

• 批量梯度下降(Batch Gradient Descent，BGD)：梯度下降的每一步中，都用到所有的训练样本；
• 随机梯度下降(Stochastic Gradient Descent，SGD)：梯度下降的每一步中，用到一个样本，在每一次计算后，便更新参数，不需要首先将所有的训练集求和；
• 小批量梯度下降(Mini-Batch Gradient Descent，MBGD)：梯度下降的每一步中，用到一定批量的训练样本；

3.1 批量梯度下降(Batch Gradient Descent)

• 参数更新：
  $${\omega }_j:={\omega }_j-\alpha \frac{1}{m}\sum _{i=1}^m((h(x^{(i)})-y^{(i)})\cdot x_j^{(i)})，同步更新{\omega }_j，(j=0,1,\dots ,n)$$

3.2 随机梯度下降(Stochastic Gradient Descent)

• 推导过程：
  $$\begin{array}{rl}\omega =& \omega -\alpha \cdot \frac{\partial J(\omega )}{\partial \omega }\\ h(x)& ={\omega }^{T}X={\omega }_0{x}_0+{\omega }_1{x}_1+{\omega }_2{x}_2+\cdots +{\omega }_n{x}_n\\ J(\omega )=& \frac{1}{2}(h(x^{(i)})-y^{(i)}{)}^2\\ \frac{\partial }{\partial {\omega }_j}J(\omega )=& \frac{\partial }{\partial {\omega }_j}\frac{1}{2}(h(x^{(i)})-y^{(i)}{)}^2\\ =& 2\cdot \frac{1}{2}(h(x^{(i)})-y^{(i)})\cdot \frac{\partial }{\partial {\omega }_j}(h(x^{(i)})-y^{(i)})\\ =& (h(x^{(i)})-y^{(i)})\cdot \frac{\partial }{\partial {\omega }_j}(\sum _{i=0}^n({\omega }_i{x}_i^{(i)}-y^{(i)}))\\ =& (h(x^{(i)})-y^{(i)})x_j^{(i)}\end{array}$$
• 参数更新：
  $${\omega }_j:={\omega }_j-\alpha (h(x^{(i)})-y^{(i)})x_j^{(i)}，同步更新{\omega }_j(j=0，1，\dots ，n)$$

3.3 小批量梯度下降(Mini-Batch Gradient Descent)

• 参数更新：
  $${\omega }_j:={\omega }_j-\alpha \frac{1}{b}\sum _{k=i}^{i+b-1}(h(x^{(k)})-y^{(k)})x_j^{(k)}，同步更新{\omega }_j(j=0,1,2,\dots ,n)$$
• $b$的取值：
  $$\begin{array}{rl}b=& 1：随机梯度下降，SGD；\\ b=& m：批量梯度下降，BGD；\\ b=& batch\_size：小批量梯度下降，MBGD，一般是2的倍数，常见：32，64，128等；\end{array}$$

3.4 梯度下降与最小二乘法比较

• 梯度下降：需要选择学习率$\alpha$，需要多次迭代，当特征数量n大时能较好适用，适用于各种类型的模型；
• 最小二乘法：不需要选择学习率$\alpha$，一次计算得出，需要计算$(X^{T}X{)}^{-1}$，如果特征数量n较大，则运算代价大，只适用于线性模型，不适合逻辑回归等其他模型；

3.5 数据归一化/标准化

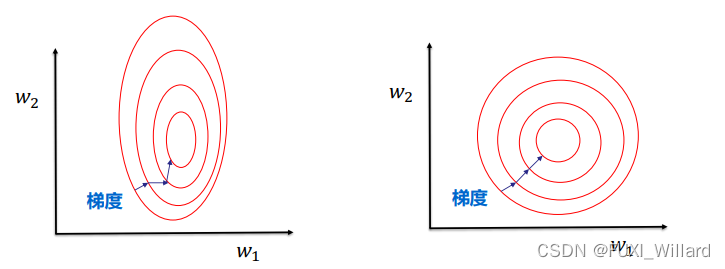
• 数据归一化可以提升模型精度：不同维度间的特征在数值上有一定比较性，可以提高分类器的准确性；
• 数据归一化可以加速模型收敛：最优解的寻优过程明显变得平缓，更容易正确的收敛到最优解；
  

3.5. 1 归一化(最大-最小规范化)

• 数据归一化：使得各特征对目标变量影响一致，会将特征数据进行伸缩变化，数据归一化会改变特征数据分布；
  $$x^{\ast }=\frac{x-x_{min}}{x_{max}-x_{min}}，将数据映射到[0,1]区间；$$

• Z-Score标准化：使得不同特征间具备可比性，经过标准化变换后特征数据分布没有发生改变；
  $$x^{\ast }=\frac{x-\mu }{\sigma }，处理后数据均值为0，方差为1；$$

3.5. 2 归一化/标准化的模型

• 需要做数据归一化/标准化的模型：

• a.线性模型：KNN(K近邻)、K-means聚类、感知机、SVM；

• 不需要做数据归一化/标准化的模型：

• a.决策树、基于决策树的Boosting和Bagging等集成学习模型；

• b.随机森林、XGBoost、LightGBM等树模型；

• c.朴素贝叶斯；