• 实验目的

1. 掌握有信息搜索策略的算法思想；

2. 能够编程实现搜索算法；

3. 应用A*搜索算法求解罗马尼亚问题。

• 实验环境

使用python编程实现，并在Mindspore框架下实现。

• 罗马尼亚问题说明

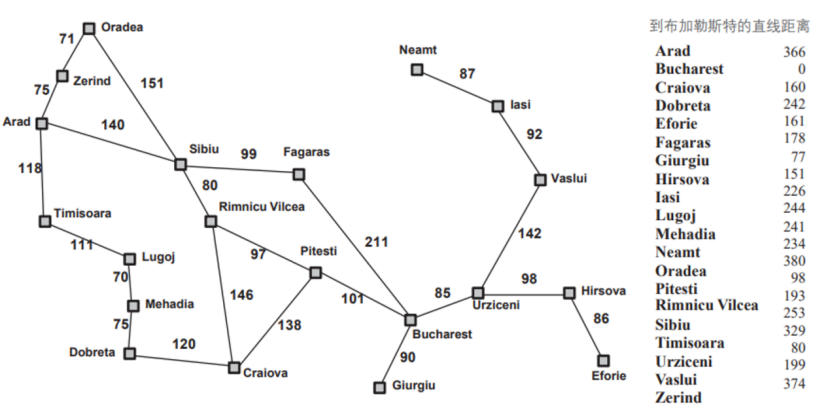
agent在罗马尼亚度假，目前位于 Arad 城市。agent明天有航班从Bucharest 起飞，不能改签退票。

现在你需要寻找到 Bucharest 的最短路径，在右侧编辑器补充void A_star(int goal,node &src,Graph &graph)函数，使用编写的搜索算法代码求解罗马尼亚问题：

• 实验原理

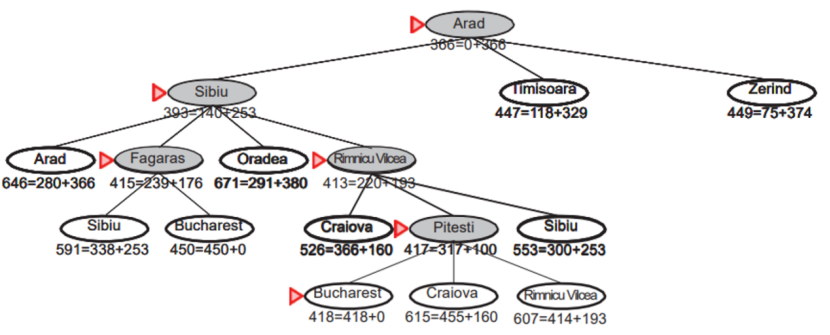
（1）A*算法的原理是设计一个评价估计函数：其中评估函数f(n)是从起始节点通过节点n的到达目标节点的最小代价路径的估计值，函数g(n)是从起始节点到n节点的已走过路径的实际代价，函数h(n)是从n节点到目标节点可能的最优路径的估计代价 。函数 h(n)表明了算法使用的启发信息，它来源于人们对路径规划问题的认识，依赖某种经验估计。根据 f(n)可以计算出当前节点的代价，并可以对下一次能够到达的节点进行评估。采用每次搜索都找到代价值最小的点再继续往外搜索的过程，一步一步找到最优路径。

（2）根据题目要求，得到搜索树：初始给定出发节点，放入队列中，然后进行扩展操作。

• 实验内容及步骤

1. 创建搜索树：通过递归创建节点（Node）来构建的

Node 类是实现 A* 搜索算法中的核心组件之一，代表搜索树中的一个节点，每个节点包含以下属性和方法：

属性：

• state：节点的状态，通常是问题域中的一个具体位置或配置。
• parent：指向该节点的父节点，用于回溯找到路径。
• action：从父节点到该节点所采取的动作。
• path_cost：从起始节点到当前节点的路径代价。
• depth：节点在搜索树中的深度，从根节点（深度为0）开始计算。

方法：

• Init：初始化节点的属性。如果存在父节点，则当前节点的深度是父节点的深度加1。
• repr：返回节点的字符串表示，方便打印和调试。
• lt：定义节点的小于比较，基于节点的状态，用于排序。
• expand：扩展当前节点，生成所有可能的子节点。调用 problem.actions(self.state) 获取所有可能的动作，然后对每个动作生成一个子节点。
• child_node：根据给定的动作生成一个子节点。调用 problem.result(self.state, action) 获取动作的结果状态，然后创建一个新的 Node 实例。
• solution：从当前节点回溯到根节点，获取路径上的所有状态。使用 self.path() 方法回溯路径，并返回路径上的状态列表。
• path：回溯当前节点到根节点的路径。使用递归或循环方式回溯到根节点，并返回路径上的节点列表。
• eq：定义节点的等价性，基于节点的状态。用于比较两个节点是否相等。
• hash：为节点定义哈希值，基于节点的状态。允许节点被用作哈希表的键，在字典中存储节点。

1. 实现A*搜索算法：

首先，在实现A*算法之前，定义了一个抽象基类Problem类，它定义了使用 A* 搜索算法解决问题时所需的接口和基本框架。具体的问题实现需要继承这个类，并实现其中的抽象方法。以下是每个方法的简要说明：

• init：初始化问题实例，需要提供初始状态 initial 和（可选的）目标状态 goal。
• Actions：抽象方法，需要在子类中实现。该方法应该返回给定状态 state 下所有可能的动作。
• Result：抽象方法，需要在子类中实现。该方法应该根据当前状态 state 和一个动作 action 计算出新的状态。
• goal_test：检查给定状态 state 是否是目标状态。如果 goal 是一个列表，使用 is_in 函数（需要在外部定义）检查状态是否在列表中；否则，直接比较状态是否相等。
• path_cost：计算从状态 state1 通过动作 action 到状态 state2 的路径代价。这里简单地将代价设为前一个代价 c 加 1，实际应用中可能需要根据具体情况计算代价。
• value：抽象方法，需要在子类中实现。该方法应该返回给定状态 state 的启发式估计值，即从该状态到目标状态的估计代价。

A*算法的实现：

函数定义：astar_search 函数接受一个 problem 对象作为参数，这个对象包含了问题的定义，包括初始状态、目标状态、可能的动作、状态转移函数、路径代价计算函数等。

1. 初始化
2. 进入循环，直到找到目标节点或开放列表为空。

• 节点扩展：从 frontier 中取出成本最低的节点（这里是列表的第一个元素）。如果这个节点是目标节点，打印出路径代价，并返回路径。将节点从 frontier 中移除，并添加到 explored 列表中。
• 子节点生成：对于当前节点的每个邻居，生成一个新的子节点。计算子节点的路径代价，包括从起点到当前节点的代价加上从当前节点到子节点的代价。
• 子节点检查和更新：检查子节点是否已经在 explored 或 frontier 中：如果不在，将子节点添加到 frontier 中。如果已存在，但新计算的路径代价更低，则更新该节点的路径代价。
• 排序：对 frontier 中的节点根据其路径代价和启发式代价（即到目标的直线距离）进行排序，以确保下一个循环中能够优先处理代价最低的节点。

3.使用编写的搜索算法代码求解罗马尼亚问题：

1. 定义问题Problem类
2. 定义Node节点
3. 定义罗马尼亚地图问题的数据结构

包括但不限于：

• neighbor_map：城市之间的邻居关系。

• neighbormapWithweight：带权重的城市邻居关系，表示城市间的距离

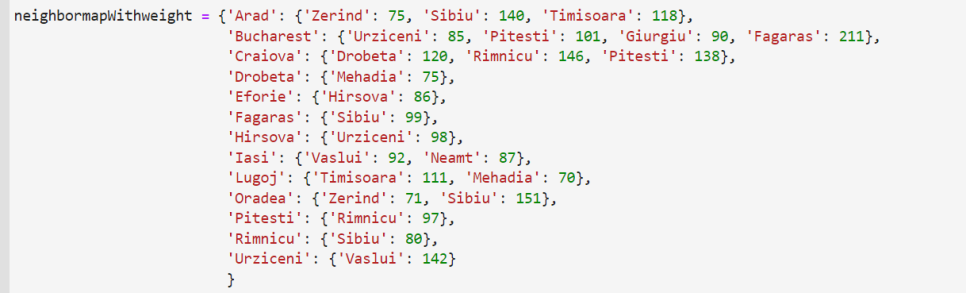
• romania_map_locations：城市的坐标。

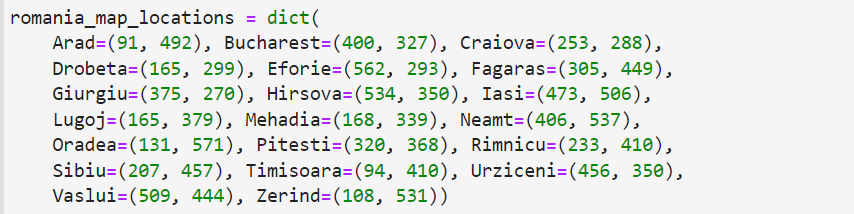
• straight_line_distance_to_Bucharest：每个城市到目标城市的直线距离。

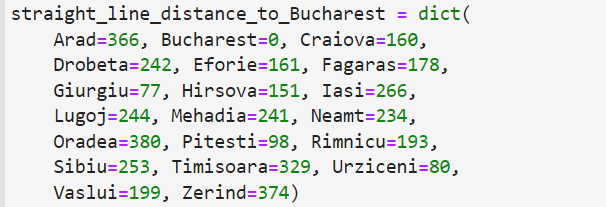
• city_neighbor：每个城市的所有邻居及其权重。

构建完整的邻居关系：

• start_to_goal_distance：每个城市到目标城市的直线距离。

计算每个城市到目标城市的距离：

1. A*算法
2. 实现并输出A*搜索的路径

import math
import sys
from collections import deque


class Problem:
    #初始化问题实例
    def __init__(self, initial, goal=None):
        self.initial = initial
        self.goal = goal
    #返回给定状态下所有可能的动作
    def actions(self, state):
        raise NotImplementedError
    #根据当前状态和一个动作计算出新的状态。
    def result(self, state, action):
        raise NotImplementedError
    #检查给定状态是否是目标状态
    def goal_test(self, state):
        if isinstance(self.goal, list):
            return is_in(state, self.goal)
        else:
            return state == self.goal
    #计算从状态state1通过动作action到状态state2的路径代价
    def path_cost(self, c, state1, action, state2):
        return c + 1
    #返回给定状态的启发式估计值
    def value(self, state):
        raise NotImplementedError

class Node:
    #初始化节点属性
    def __init__(self, state, parent=None, action=None, path_cost=0):
        self.state = state
        self.parent = parent
        self.action = action
        self.path_cost = path_cost
        self.depth = 0
        if parent:
            self.depth = parent.depth + 1
    #返回节点的字符串表示
    def __repr__(self):
        return "<Node {}>".format(self.state)
    #比较
    def __lt__(self, node):
        return self.state < node.state
    #扩展当前节点
    def expand(self, problem):
        return [self.child_node(problem, action)
                for action in problem.actions(self.state)]
    #根据给定动作生成一个子节点
    def child_node(self, problem, action):
        next_state = problem.result(self.state, action)
        next_node = Node(next_state, self, action, problem.path_cost(self.path_cost, self.state, action, next_state))
        return next_node
    #回溯到根节点
    def solution(self):
        return [node.state for node in self.path()[0:]]
    #回溯当前节点到根节点的路径
    def path(self):
        node, path_back = self, []
        while node:
            path_back.append(node)
            node = node.parent
        return list(reversed(path_back))
    #比较两个节点是否相等
    def __eq__(self, other):
        return isinstance(other, Node) and self.state == other.state
    #存储节点
    def __hash__(self):
        return hash(self.state)

neighbor_map = {'Arad': ['Zerind', 'Sibiu', 'Timisoara'], 'Bucharest': ['Urziceni', 'Pitesti', 'Giurgiu', 'Fagaras'],
                'Craiova': ['Drobeta', 'Rimnicu', 'Pitesti'], 'Drobeta': ['Mehadia'], 'Eforie': ['Hirsova'],
                'Fagaras': ['Sibiu'], 'Hirsova': ['Urziceni'], 'Iasi': ['Vaslui', 'Neamt'],
                'Lugoj': ['Timisoara', 'Mehadia'],
                'Oradea': ['Zerind', 'Sibiu'], 'Pitesti': ['Rimnicu'], 'Rimnicu': ['Sibiu'], 'Urziceni': ['Vaslui']}

neighbormapWithweight = {'Arad': {'Zerind': 75, 'Sibiu': 140, 'Timisoara': 118},
                         'Bucharest': {'Urziceni': 85, 'Pitesti': 101, 'Giurgiu': 90, 'Fagaras': 211},
                         'Craiova': {'Drobeta': 120, 'Rimnicu': 146, 'Pitesti': 138},
                         'Drobeta': {'Mehadia': 75},
                         'Eforie': {'Hirsova': 86},
                         'Fagaras': {'Sibiu': 99},
                         'Hirsova': {'Urziceni': 98},
                         'Iasi': {'Vaslui': 92, 'Neamt': 87},
                         'Lugoj': {'Timisoara': 111, 'Mehadia': 70},
                         'Oradea': {'Zerind': 71, 'Sibiu': 151},
                         'Pitesti': {'Rimnicu': 97},
                         'Rimnicu': {'Sibiu': 80},
                         'Urziceni': {'Vaslui': 142}
                         }

romania_map_locations = dict(
    Arad=(91, 492), Bucharest=(400, 327), Craiova=(253, 288),
    Drobeta=(165, 299), Eforie=(562, 293), Fagaras=(305, 449),
    Giurgiu=(375, 270), Hirsova=(534, 350), Iasi=(473, 506),
    Lugoj=(165, 379), Mehadia=(168, 339), Neamt=(406, 537),
    Oradea=(131, 571), Pitesti=(320, 368), Rimnicu=(233, 410),
    Sibiu=(207, 457), Timisoara=(94, 410), Urziceni=(456, 350),
    Vaslui=(509, 444), Zerind=(108, 531))

straight_line_distance_to_Bucharest = dict(
    Arad=366, Bucharest=0, Craiova=160,
    Drobeta=242, Eforie=161, Fagaras=178,
    Giurgiu=77, Hirsova=151, Iasi=266,
    Lugoj=244, Mehadia=241, Neamt=234,
    Oradea=380, Pitesti=98, Rimnicu=193,
    Sibiu=253, Timisoara=329, Urziceni=80,
    Vaslui=199, Zerind=374)

"""将通过每一个城市都可以找到它的邻居"""
all_city_neighbor = set(neighbor_map)

for i in neighbor_map:
    for a_city in neighbor_map[i]:
        if a_city not in all_city_neighbor:
            all_city_neighbor.add(a_city)

city_neighbor = {a: {} for a in all_city_neighbor}

for i in city_neighbor:
    if i in neighbormapWithweight:
        city_neighbor[i] = neighbormapWithweight[i]
for i in city_neighbor:
    for j in neighbormapWithweight:
        if i in neighbormapWithweight[j]:
            city_neighbor[i][j] = neighbormapWithweight[j][i]

start = "Arad"
goal = "Bucharest"

start_to_goal_distance = dict()
for i in romania_map_locations:
    """用直线距离"""
    start_to_goal_distance[i] = math.sqrt((romania_map_locations[i][0] - romania_map_locations[goal][0]) ** 2
                                          + (romania_map_locations[i][1] - romania_map_locations[goal][1]) ** 2)

"""A*搜索"""
def astar_search(problem):
    node_new = Node(problem.initial)  # 初始化node结点
    frontier = []  # frontier表的初始化
    frontier.append(node_new)  # 添加初始结点
    explored = []  # explored表初始化

    while True:
        # 当frontier表中没有结果时返回失败
        if len(frontier) == 0:
            return
        # 从frontier表中取出最优的结点拓展
        node_new = frontier[0]
        # 从frontier表中删除已经拓展的结点
        del frontier[0]
        # 若找到目标结点则对路径进行输出
        if problem.goal_test(node_new.state):
            print("最小的代价值为", node_new.path_cost)
            return node_new.solution()
        # 将已经搜索表拓展新的结点
        explored.append(node_new)
        # 搜索并拓展新的frontier表
        for p in city_neighbor[node_new.state]:
            child = Node(p, node_new, None, (city_neighbor[node_new.state][p] + node_new.path_cost))
            # 如果新的子结点不在explored和frontier中，则在frontier表中加入新的拓展结点
            figure = 0
            for i in explored or frontier:
                if i.state == child.state:
                    figure += 1
            if figure <= 0:
            # if child.state not in explored or frontier:
                frontier.append(Node(child.state, node_new, None, child.path_cost))
            # 如果新结点在frontier中，则更新其一致代价
            else:
                for i in frontier:
                    if i.state == child.state:
                        if i.path_cost < child.path_cost:
                            i.path_cost = child.path_cost
                            break
        # 对新加入的结点或者更新的结点进行排序
        frontier = sorted(frontier, key=lambda x: x.path_cost + start_to_goal_distance[x.state])

"""实现并输出A*搜索的路径"""
romania_problem = Problem(start, goal)
road = astar_search(romania_problem)
print(road)

1. 分析算法的时间复杂度。

1. 考虑节点扩展：对于每个节点，算法需要遍历其所有邻居。在罗马尼亚地图问题中，每个城市的平均邻居数量是有限的，我们可以假设每个城市大约有 k 个邻居。因此，对于 n 个城市，算法可能需要扩展 n * k 个节点。
2. 启发式函数评估：启发式函数是基于每个城市到目标城市的直线距离，对于每个节点，启发式函数的评估是常数时间 O(1)。
3. 排序操作：每次扩展节点后，需要对开放列表进行排序。最坏情况下，开放列表中有 n 个节点，排序的时间复杂度是 O(n log n)。在每一层搜索中，排序操作可能被执行多次，但通常排序的次数不会超过搜索的深度。

所以，时间复杂度为： O(n * k * n log n)。

• 实验结果：

• 思考题

1. 宽度优先搜索，深度优先搜索，一致代价搜索，迭代加深的深度优先搜索算法哪种方法最优？

• 宽度优先搜索（BFS）：

优点：保证找到的路径是最短的（如果存在解）。

缺点：在广度上扩展，可能需要很大的内存空间，特别是在深搜问题中。

适用场景：目标节点离起点不远，或者图的分支不深的问题。

• 深度优先搜索（DFS）：

优点：内存消耗较小，因为它一次只扩展一个分支。

缺点：可能找不到最短路径，且可能陷入无法到达目标的无限深的分支。

适用场景：目标节点在起点的特定方向上，或者需要探索所有可能路径的问题。

• 一致代价搜索：

优点：每次扩展代价相同的节点，可以看作是BFS的一种优化，减少了需要存储的节点数。

缺点：在某些情况下可能不如BFS直观。

适用场景：当所有步骤的代价相同时，可以优化BFS。

• 迭代加深的深度优先搜索（IDDFS）：

优点：结合了DFS和BFS的优点，通过限制搜索深度来逐步扩展搜索范围。

缺点：实现较为复杂，且在最坏情况下可能与DFS一样糟糕。

适用场景：适用于那些目标深度未知或者变化的问题。

它们各自适合不同的场景。选择哪种算法取决于具体问题的性质，如搜索空间的大小、解的路径长度、内存限制等。

2.贪婪最佳优先搜索和A*搜索那种方法最优？

1. 从完备性角度上分析，因为测试的数据很少，所以无论是贪婪最佳优先搜索和A算法都可以找到最终的解，但是由于贪婪最佳优先搜索的性质，存在无解的情况，而A算法在满足一致性条件和可采纳性条件的情况下一定能求出解。
2. 从最优性角度上分析：通过罗马尼亚旅游问题可以看出，A*搜索算法的结果要明显优于贪婪最佳优先搜索，并且在满足一致性条件和可采纳性条件的基础上可以求出最优解。
3. 从时间和空间复杂度角度上分析：因为这两种算法虽然搜索的算法是相似的，A*是贪婪最佳优先算法的优化算法，只有启发函数的判断存在差异，所以时间和空间复杂度可以判断为相同。

3. 分析比较无信息搜索策略和有信息搜索策略。

无信息：无信息搜索策略不使用或无法使用关于搜索空间的额外信息（如启发式信息）来指导搜索。如：宽度优先搜索，深度优先搜索等。实现简单，不需要对问题域有深入了解。可能需要探索巨大的搜索空间，特别是在解空间很大时。也无法保证找到最优解，尤其是在代价不同的路径中。

有信息：有信息搜索策略使用关于搜索空间的额外信息（启发式信息）来指导搜索。如：贪婪最佳优先搜索，A*搜索。通常比无信息搜索策略更高效，因为它们使用启发式信息来减少搜索空间。A*搜索在启发式函数满足某些条件时可以保证找到最优解。实现比无信息搜索策略复杂，需要设计和实现启发式函数。性能依赖于启发式函数的质量，不好的启发式函数可能导致性能下降。

实验收获

1. 学习到如何使用优先队列（代码使用了列表和排序来模拟优先队列的行为）来存储待探索的节点，以及如何使用已探索列表来避免重复探索相同的节点。
2. 学习到A*算法的原理，更加深入的理解到它如何结合实际代价（g(n)）和启发式估计（h(n)）来寻找最优路径。
3. 思考题中比较无信息搜索的几种方法，有信息搜索的两种方法，并比较了有无信息搜索；能够让我们学习搜索算法更加系统化。