全连接神经网络-学习笔记汇总,包含定义,公式,python代码实现
本文介绍了全连接神经网络的基本结构与工作原理。全连接神经网络由输入层、隐藏层和输出层组成,其中每一层的神经元都与上一层所有神经元相连。文章详细分析了神经网络单元结构,指出不激活时为线性回归模型,使用Sigmoid激活函数则变为逻辑回归模型。 重点讨论了激活函数的作用与类型,包括: Linear函数:适用于回归任务 Sigmoid函数:适用于二分类,但存在梯度消失问题 Tanh函数:改进Sigmoi
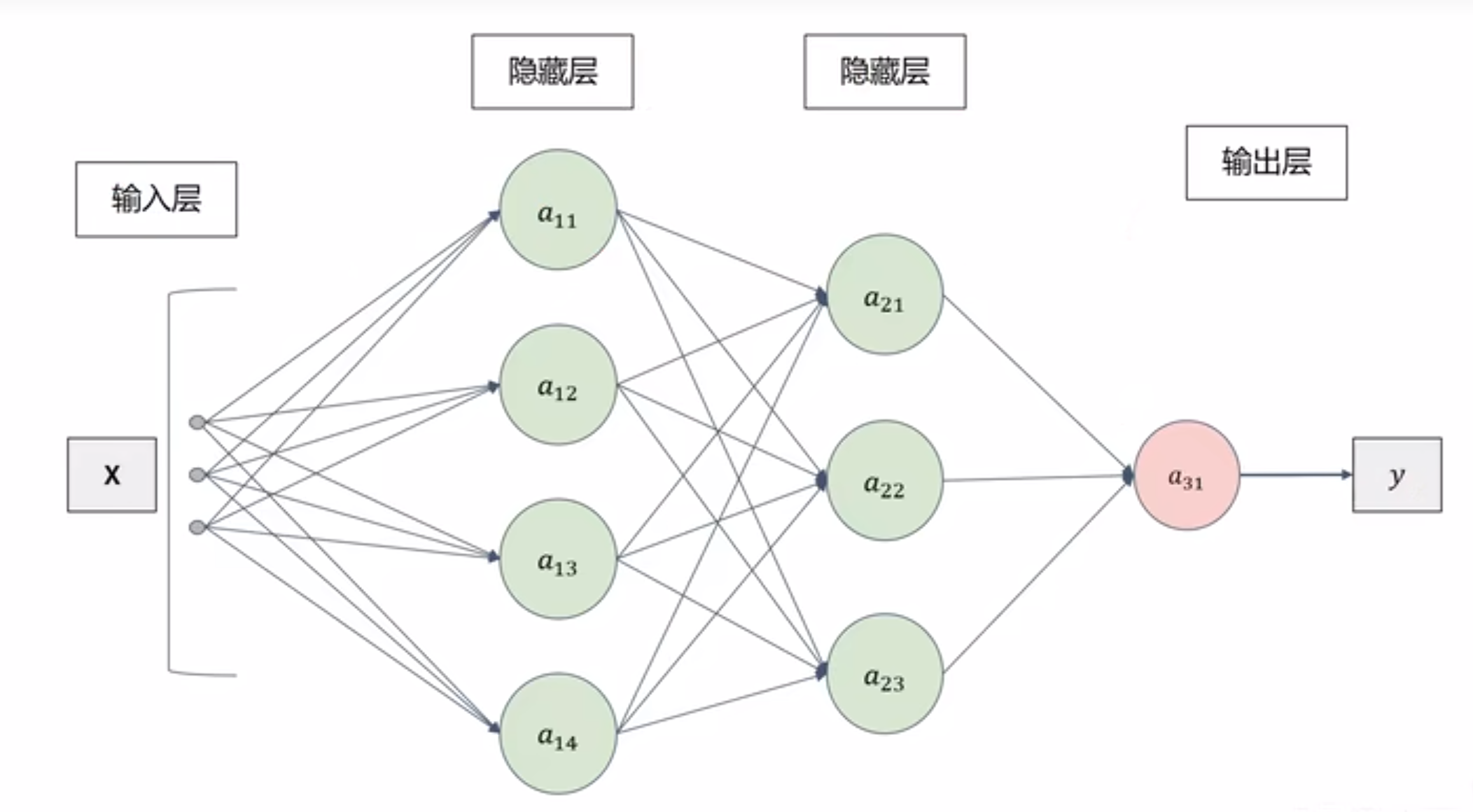
全连接神经网络
全连接:每一层的神经元都与上一层的所有神经元相连接
整体结构
分为输入层,隐藏层,输出层
隐藏层层数视任务而定:可以是1层,也可以是很多层
输出层可以有一个输出也可以是 多个输出
单元结构
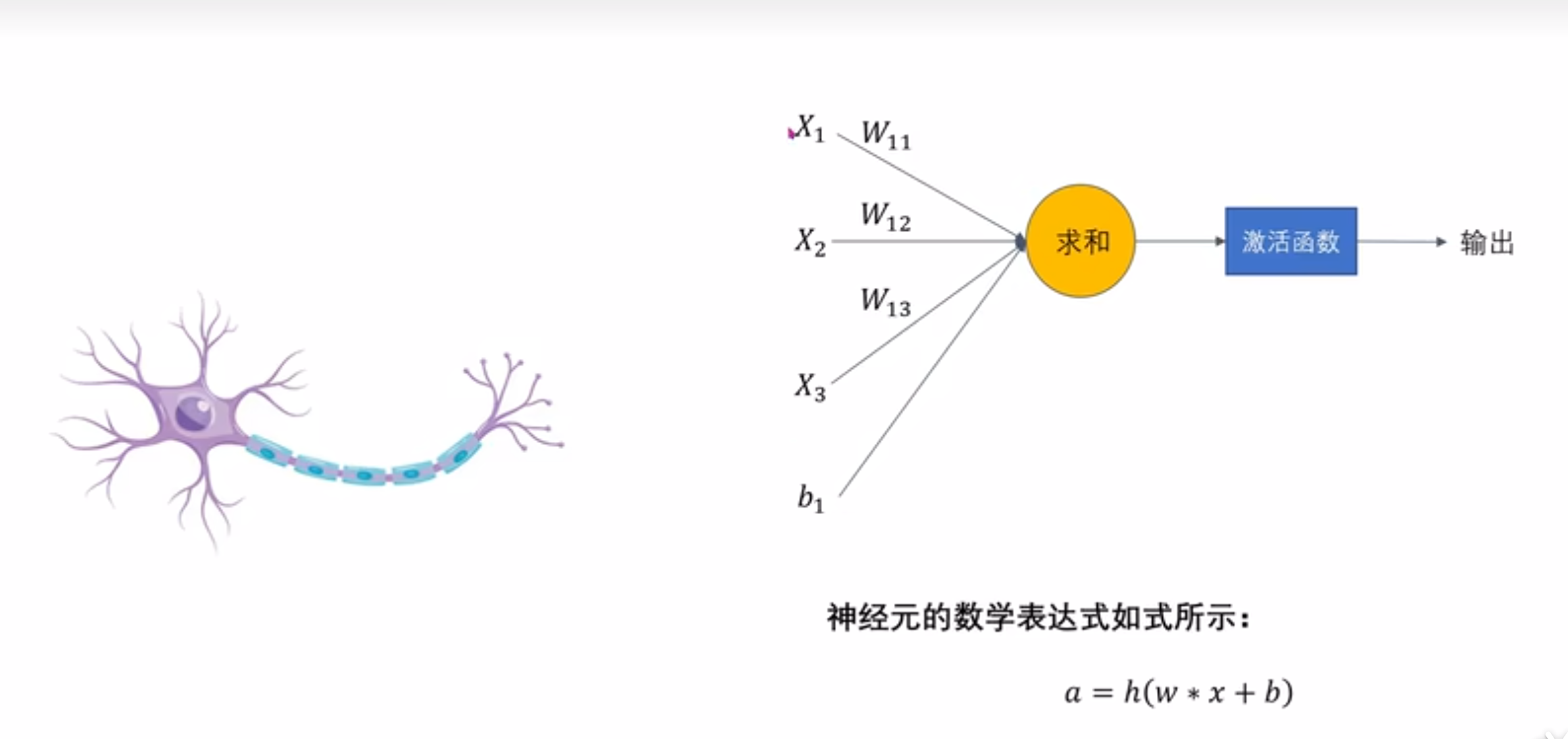
数学表达式:
a=h(wTX+b)=h(w1x1+⋯+wnxn+b)h()就是激活函数,是一个非线性函数wTX+b就是前面的线性回归 a = h(w^TX+b)=h(w_1x_1+\dots+w_nx_n+b) \\ h()就是激活函数,是一个非线性函数 \\ w^TX+b就是前面的线性回归 a=h(wTX+b)=h(w1x1+⋯+wnxn+b)h()就是激活函数,是一个非线性函数wTX+b就是前面的线性回归
思考:全连接神经网络的单元结构就是
如果不经过激活函数,那就是线性回归
a=wTX+b a = w^TX+b a=wTX+b
如果激活函数是sigmoid函数
a=σ(wTX+b) a = \sigma(w^TX+b) a=σ(wTX+b)
那就变成逻辑回归了
激活函数
作用
引入了激活函数,网络才具有学习更加复杂关系能力的原因,由前面的思考得到,如果去掉了激活函数,那么单元结构就会变成一个线性回归模型,这样网络学习能力就会受限
为什么激活函数不是线性函数?
以一个小例子:数学表达式为a=h(x)=cx,单元结构如下
X->a11->a21->a31->y
有两个隐藏层
a11=cxa21=ca11=c2xa31=ca21=c3x a_{11}=cx \\ a_{21} = ca_{11}=c^2x \\ a_{31}=ca_{21}=c^3x a11=cxa21=ca11=c2xa31=ca21=c3x
我们发现,最终结果还是一个线性的,我们可以直接把单元结构改成
X->a31->y
数学表达式为
a=h(x)=kx=c3x a=h(x)=kx=c^3x a=h(x)=kx=c3x
那么两个隐藏层就被抵消掉了;隐藏层的作用是为了执行更复杂的计算任务,但使用线性函数作为激活函数,不仅浪费了计算资源还没起什么作用,等价于没有隐藏层的单元结构
分类
Linear
线性函数,相当于没有使用激活函数
y=g(z)=z=w⃗x⃗+b y = g(z) = z=\vec{w}\vec{x}+b y=g(z)=z=wx+b
适用于:回归模型,比如预测房价
python实现单隐藏层的前向传播
使用numpy手动实现
def g(w, x, b):
return np.dot(w, x) + b
def dense(a_in, W, B, g):
a_out = np.zeros(W.shape[0])
for i in range(a_in.shape[0]):
w = W[i, :]
a_out[i] = g(w, a_in, B[i])
return a_out
使用tensorflow
用到的库
import numpy as np
import tensorflow as tf
# 层模型:units:神经元数 activation:激活函数类别
from tensorflow.keras.layers import Dense
# 顺序模型
from tensorflow.keras.models import Sequential
# 特征 shape=(1,2)
X = np.array([[2, 1]])
# 标签 shape=(1,)
Y = np.array([7])
# 隐藏层,3个神经元,使用线性激活函数
layer1 = Dense(units=3, activation="linear")
layer2 = Dense(units=1, activation="linear")
model = Sequential(
[
# 显式声明,不推荐
layer1, layer2
]
)
# 编译模型 loss使用均方误差MSE
model.compile(
loss=tf.keras.metrics.mean_squared_error
)
# print(X.reshape(-1, 1))
# print(Y.reshape(-1, 1).shape)
# fit实现前向传播;其实fit的功能包括前向传播,反向传播,参数更新
model.fit(X, Y,epochs=1000)
#输出模型结构
model.summary()
# 输出预测值
print(model.predict(X))
sigmoid函数
y=11+e−zy′=y(1−y) y = \frac{1}{1+e^{-z}} \\ y' = y(1-y) y=1+e−z1y′=y(1−y)
绘制图像:
import numpy as np
import matplotlib.pyplot as plt
x_list = []
sig_list = []
d_sig_list = []
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_de(x):
sig = sigmoid(x)
return sig*(1 - sig)
for x in np.arange(-10, 11, 0.1):
x_list.append(x)
sigm = sigmoid(x)
desig = sigmoid_de(x)
sig_list.append(sigm)
d_sig_list.append(desig)
plt.plot(x_list, sig_list,label="sigmoid")
plt.plot(x_list, d_sig_list,label="sigmoid'")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.grid(True)
plt.show()
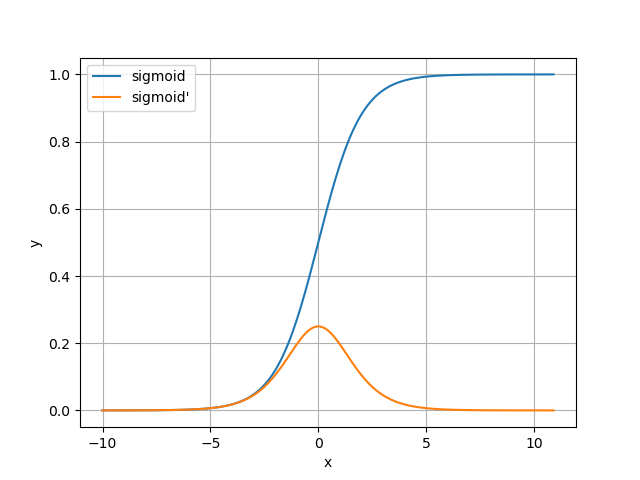
分析:
sigmoid导数图像两侧都趋近于0,就导致偏离对称轴一定距离后,梯度值会变得很小,这就会导致梯度下降时参数更新的慢
优点:
1.简单,非常适用于二分类分类任务
缺点:
1.反向传播训练时有梯度消失的问题
(什么是反向传播?使用链式法则将损失函数对参数的梯度逐层回传,用于更新参数和偏置)
比如这样
w=w−α∂J∂wsigmoid导数的最大值是0.25,我们假设梯度就是0.25对于很多隐藏层的网络结构,反向传播时就会这样w=w−α(0.25∗0.25∗⋯∗0.25)梯度就变得很小很小,也就是梯度消失问题 w = w - \alpha\frac{\partial J}{\partial w} \\ sigmoid导数的最大值是0.25,我们假设梯度就是0.25 \\ 对于很多隐藏层的网络结构,反向传播时就会这样 \\ w = w-\alpha(0.25*0.25*\dots*0.25) \\ 梯度就变得很小很小,也就是梯度消失问题 w=w−α∂w∂Jsigmoid导数的最大值是0.25,我们假设梯度就是0.25对于很多隐藏层的网络结构,反向传播时就会这样w=w−α(0.25∗0.25∗⋯∗0.25)梯度就变得很小很小,也就是梯度消失问题
2.输出值区间为(0,1),关于原点不对称,会使参数更新的比较慢
(所以我们希望的激活函数是关于原点对称的,即奇函数f(-x) = -f(x))
3.梯度更新在不同方向走的太远(导数图像对称轴两侧),使优化难度增大,训练耗时
Tanh函数
双曲正切激活函数
y=ez−e−zez+e−zy′=1−y2 y = \frac{e^z-e^{-z}}{e^z+e^{-z}} \\ y' = 1-y^2 y=ez+e−zez−e−zy′=1−y2
import numpy as np
import matplotlib.pyplot as plt
w = 0.5
b = 0.1
x_list = []
y_list = []
de_y_list = []
def get_z(x, w, b):
return w * x + b
def tanh(x, w, b):
z = get_z(x, w, b)
frac1 = np.exp(z) - np.exp(-z)
frac2 = np.exp(z) + np.exp(-z)
return frac1 / frac2
def de_tanh(y):
return 1 - y ** 2
for x in np.arange(-10.0, 10.1, 0.1):
x_list.append(x)
y = tanh(x, w, b)
y_list.append(y)
de_y = de_tanh(y)
de_y_list.append(de_y)
plt.plot(x_list,y_list,label="tanh")
plt.plot(x_list,de_y_list,label="de_tanh")
plt.legend()
plt.grid(True)
plt.show()
图像:
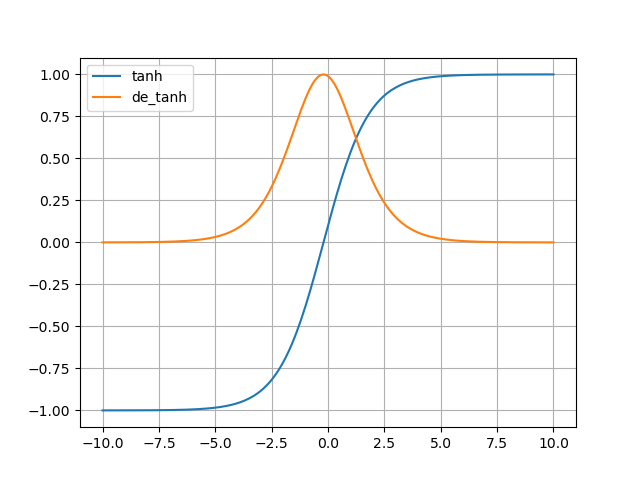
分析:原函数关于原点对称了,原函数取值(-1,1);导数图像与sigmoid的导数类似,x趋近±∞时导数趋于0
优点:
1.解决了sigmoid不关于原点对称的问题,参数更新得更快
2.导数(梯度)最大值为1,因此训练的速度高于sigmoid
缺点:
1.仍存在梯度消失的问题
(尽管梯度最大值发生变化,但图像的形状仍于sigmoid类似)
2.还是和sigmoid很类似
ReLU函数
y={z,ifz>00,ifz≤0y′={1,ifz>00,ifz≤0 y=\begin{cases} z,& if& z >0 \\ 0,&if&z\leq0 \end{cases}\\ y'=\begin{cases} 1,&if&z>0\\ 0,&if&z\leq0 \end{cases} y={z,0,ififz>0z≤0y′={1,0,ififz>0z≤0
图像
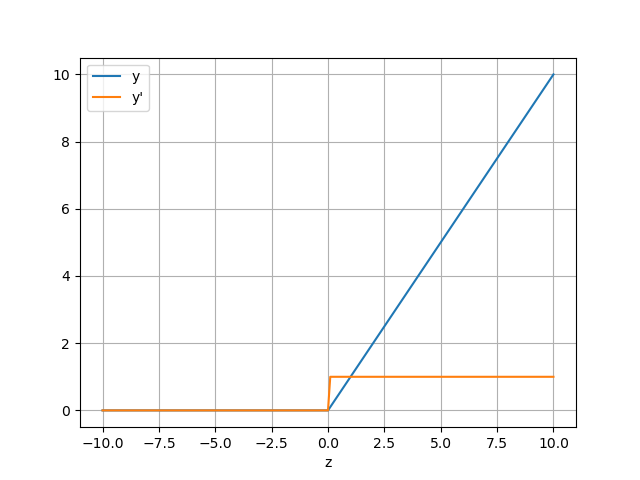
优点:
1.解决了梯度消失的问题
2.没有指数运算,计算更为简单
缺点:
1.训练时可能出现神经元死亡的情况
(当z<0时,y=0,J(w)=1/mX^T(h(z)-y),那么J对w的梯度就是0了,此时参数更新就失效了)
2.y不关于零点对称,参数更新的比较慢
适用于:输出值y只能取非负值
Leaky ReLU函数
y={z,ifz>0az,ifz≤0y′={1,ifz>0a,ifz≤0其中0<α≪1(通常设为0.01) y=\begin{cases} z,& if& z >0 \\ az,&if&z\leq0 \end{cases}\\ y'=\begin{cases} 1,&if&z>0\\ a,&if&z\leq0 \\ \end{cases} 其中 0<α≪1(通常设为 0.01)\\ y={z,az,ififz>0z≤0y′={1,a,ififz>0z≤0其中0<α≪1(通常设为0.01)
图像
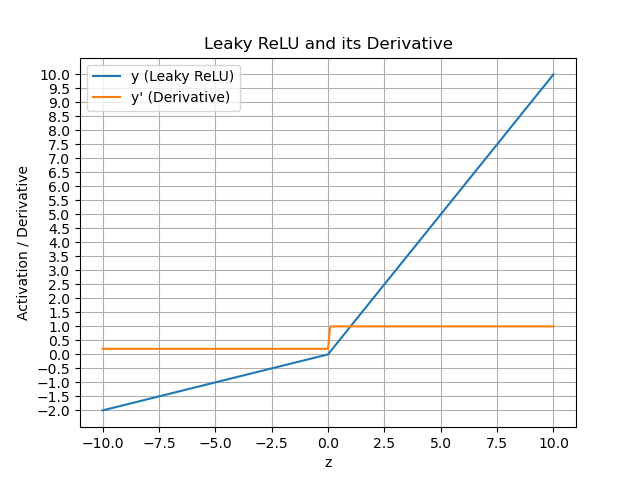
绘图代码注意事项,使用子图对象设置y轴刻度
# 获得子图对象
fig, ax = plt.subplots()
ax.plot(z_list, y_list, label="y (Leaky ReLU)")
ax.plot(z_list, de_y_list, label="y' (Derivative)")
# 设置 y 轴刻度间隔为 0.5
ax.yaxis.set_ticks(np.arange(-2, 10.1, 0.5))
ax.set_xlabel("z")
ax.set_ylabel("Activation / Derivative")
ax.set_title("Leaky ReLU and its Derivative")
ax.legend()
ax.grid(True)
plt.show()
优点:
1.解决了ReLU神经元死亡问题
(输出值以及导数都不会变为0)
缺点:
1.无法为正负输入值提供一致的关系预测(不同区间函数不同)
- 对于正输入,神经元“活跃”,直接将输入传递下去;
- 对于负输入,神经元“较弱地活跃”,只传递一小部分信号(乘以 α);
SoftMax激活函数
用于多分类问题的输出层的激活函数


给定一个输入向量z=[z1,z2,…,zn],y=1,2,…,nzi=wi⃗x⃗+biai=SoftMax(zi)=ezi∑j=1nezj 给定一个输入向量z=[z_1,z_2,\dots,z_n] ,y=1,2,\dots,n\\ z_i = \vec{w_i}\vec{x}+b_i\\ a_i=SoftMax(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n}e^{z_j}} 给定一个输入向量z=[z1,z2,…,zn],y=1,2,…,nzi=wix+biai=SoftMax(zi)=∑j=1nezjezi
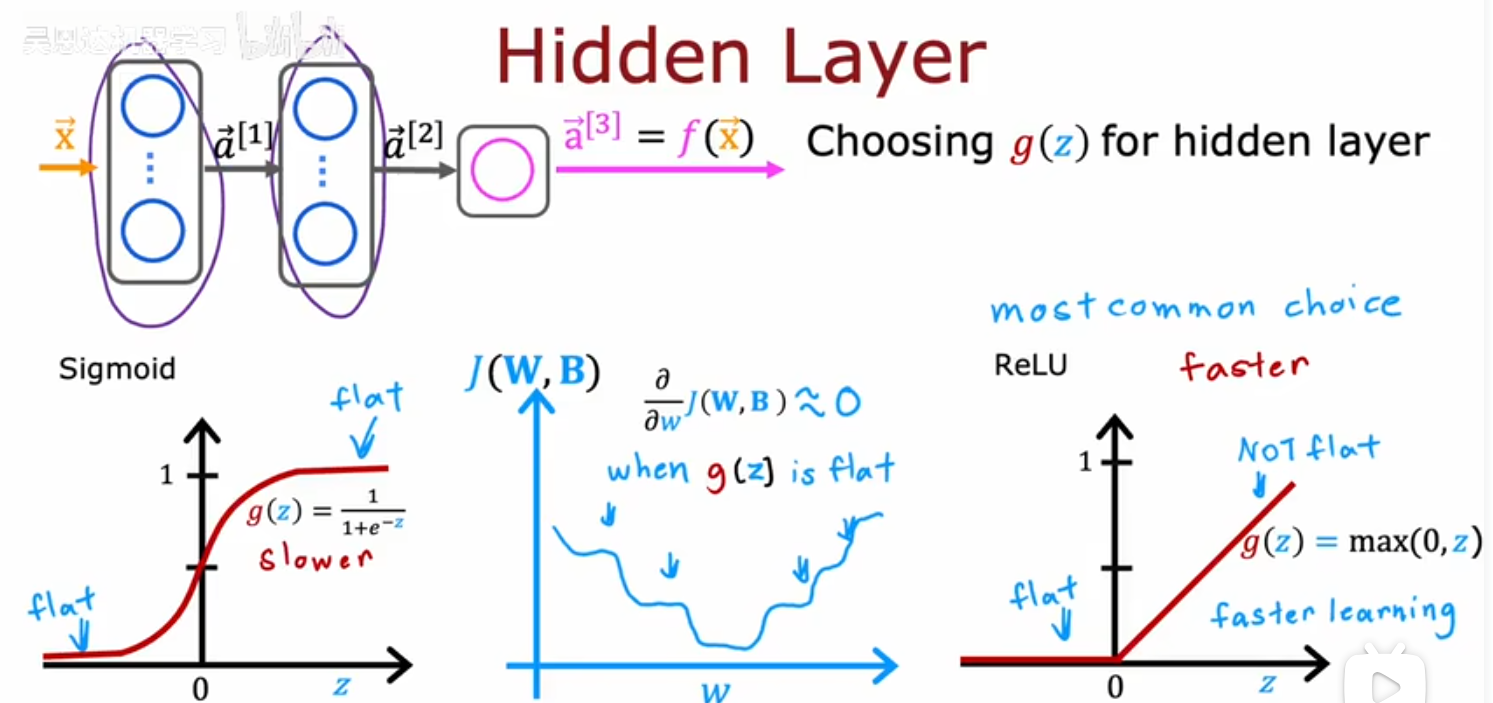
如何选择
输出层
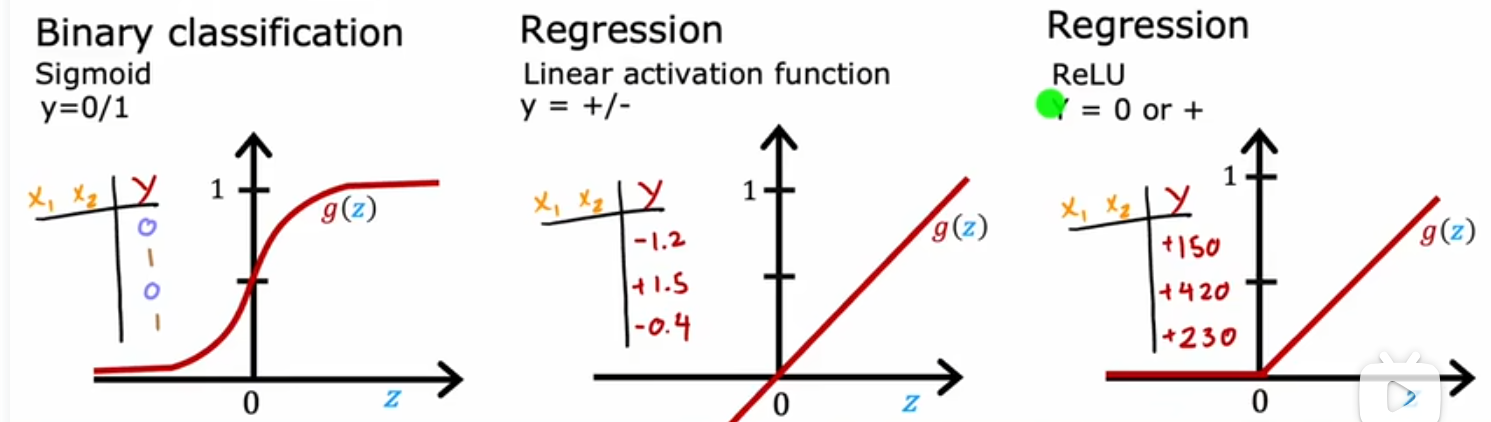
- 对于先前的预测房价之类的回归模型,激活函数用线性函数比较合适
- 对于二分类任务,比如肿瘤诊断,Minist手写数字0/1,适合使用sigmoid
- 对于输出值y非负的情况,使用ReLU
隐藏层
常用ReLU,当输出层是二分类任务时常用sigmoid
原因
- 前面介绍激活函数时提到的,计算开销
- ReLU梯度下降只会在一个方向收敛(y<0),sigmoid会在两个方向收敛(x -> -∞,x -> +∞);sigmoid这个特性会使损失函数J有许多梯度接近0的位置,不利于模型的梯度下降和参数更新
前向传播
对于线性回归和逻辑回归来说,前向传播就是计算得到回归结果的过程
对于神经网络
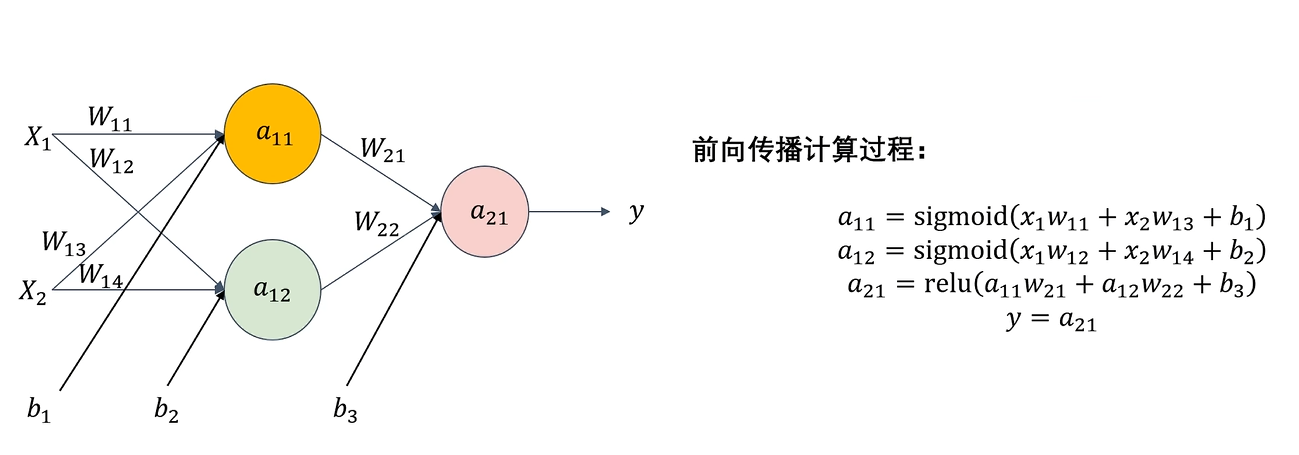
前向传播是指从输入层开始,依次经过隐藏层,最终到达输出层,逐层计算神经元输出值的过程,前向传播其实就是模型进行推理的过程
在这个过程中
- 神经元会对输入进行带权求和加上偏置(wa+b)
- 使用激活函数进行非线性变换
神经网络训练的步骤就分为:前向传播->计算误差->计算梯度->反向传播进行梯度更新
计算过程
eg:
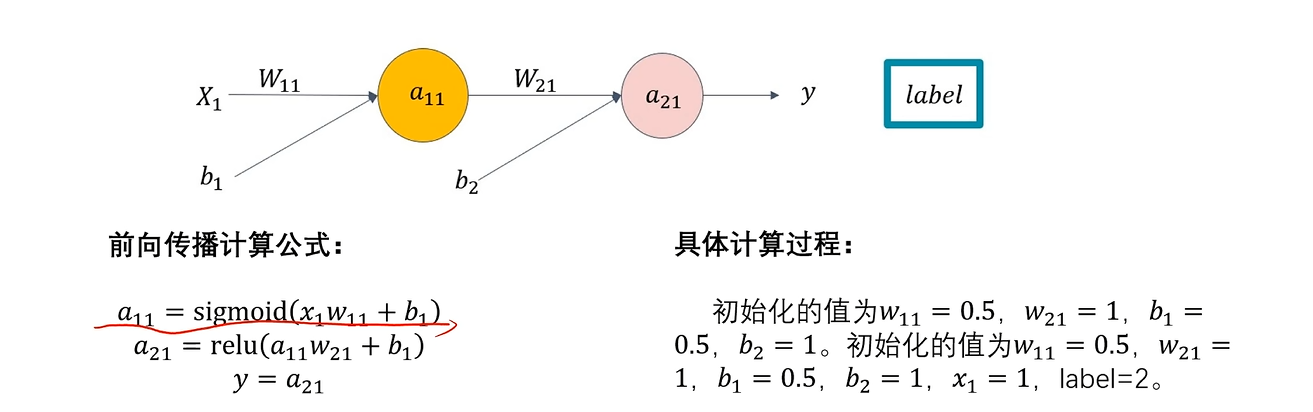
import numpy as np
# 权重
W = np.array([0.5, 1])
# 偏置
B = np.array([0.5, 1])
# 初始输入
x1 = 1
# 对应的标签
label = 1
# 带权求和
def init_z(x, w, b):
return w * x + b
# 隐藏层激活函数sigmoid
def sigmoid(a):
return 1 / (1 + np.exp(-a))
# 输出层激活函数ReLU
def ReLU(a):
if (a > 0):
return a
else:
return 0
if __name__ == '__main__':
a = x1
w = W.copy()
b = B.copy()
for i in range(len(W)):
z = init_z(a, w[i], b[i])
if i < len(W) - 1:
a = sigmoid(z)
elif i == len(W) - 1:
a = ReLU(z)
output = a
print(output)
损失函数
回顾:
线性回归模型中:均方误差损失函数:
J(w)=12m∑i=1m(wxi−yi)2 J(w) = \frac{1}{2m}\sum_{i=1}^{m}(wx_i-y_i)^2 J(w)=2m1i=1∑m(wxi−yi)2
逻辑回归中:交叉熵损失函数:
J(w)=−1m∑i=1m(yilog(σ(wTxi+b))+(1−yi)log(1−σ(wTxi+b))) J(w)= -\frac{1}{m}\sum_{i=1}^m(y_ilog(\sigma(w^Tx_i+b))+(1-y_i)log(1-\sigma(w^Tx_i+b))) J(w)=−m1i=1∑m(yilog(σ(wTxi+b))+(1−yi)log(1−σ(wTxi+b)))
链式法则
因为神经网络模型中可能存在着多层的隐藏层,当我们需要反向传播求梯度时,就涉及到对复合函数的求导,此时需要使用链式法则
单变量
y=f(u)u=g(v)v=h(x)dydx=dydududvdvdx y=f(u) \\ u = g(v) \\ v = h(x) \\ \frac{dy}{dx}=\frac{dy}{du}\frac{du}{dv}\frac{dv}{dx} y=f(u)u=g(v)v=h(x)dxdy=dudydvdudxdv
多变量
z=f(u,v)u=g(y)v=h(y)y=j(x) z = f(u,v)\\ u = g(y)\\ v = h(y) \\ y = j(x) z=f(u,v)u=g(y)v=h(y)y=j(x)
∂z∂x=∂z∂u∂u∂y∂y∂x+∂z∂v∂v∂y∂y∂x \frac{\partial z}{\partial x} = \frac{\partial z}{\partial u}\frac{\partial u}{\partial y}\frac{\partial y}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y}\frac{\partial y}{\partial x} ∂x∂z=∂u∂z∂y∂u∂x∂y+∂v∂z∂y∂v∂x∂y
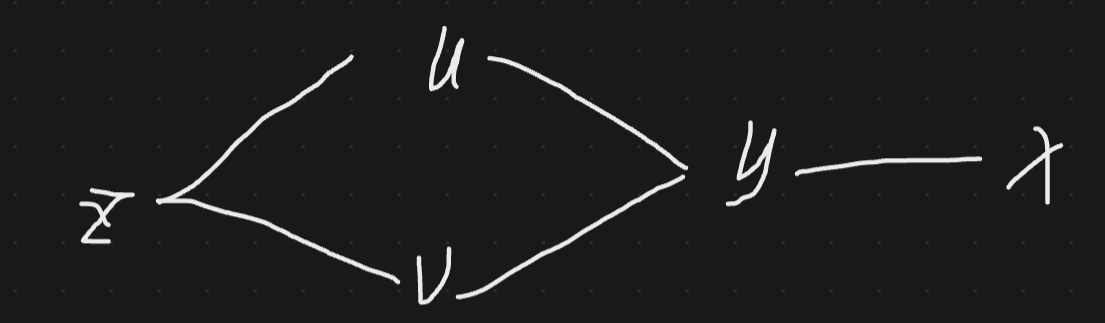
反向传播
还是前面的例子,隐藏层激活函数为sigmoid,输出层激活函数为ReLU
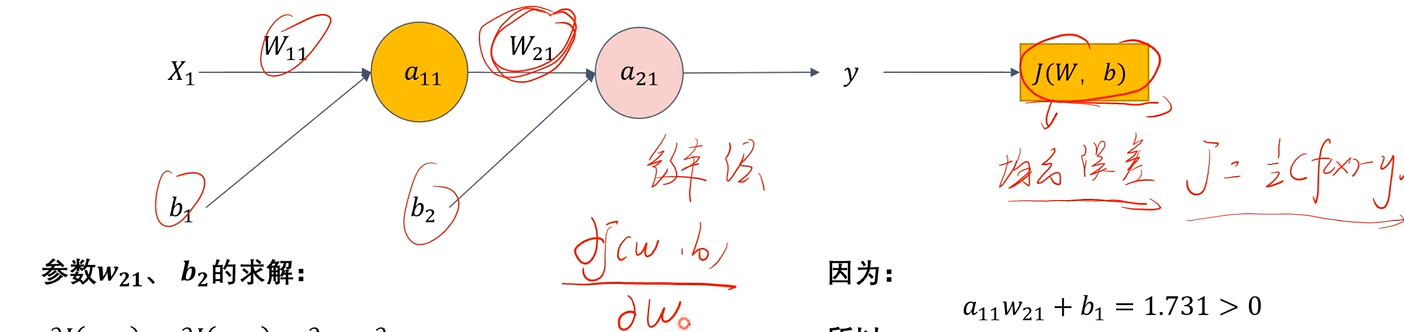
求J对w_21的梯度
∂J(w21,b)∂w21=∂J∂y∂y∂a21∂a21∂w21=∂12(y−label)2∂y∂a21∂a21∂ReLU(w21a11+b2)∂w21=(y−label)∂ReLU(w21a11+b2)∂w21a11+b2∂w21a11+b2∂w21=(y−label)×a11×∂ReLU(w21a11+b2)∂w21a11+b2 \frac{\partial J(w_{21},b)}{\partial w_{21}} = \frac{\partial J}{\partial y}\frac{\partial y}{\partial a_{21}}\frac{\partial a_{21}}{\partial w_{21}} = \frac{\partial \frac{1}{2}(y-label)^2}{\partial y}\frac{\partial a_{21}}{\partial a_{21}}\frac{\partial ReLU(w_{21}a_{11}+b_2)}{\partial w_{21}}=(y-label)\frac{\partial ReLU(w_{21}a_{11}+b_2)}{\partial w_{21}a_{11}+b_2}\frac{\partial w_{21}a_{11}+b_2}{\partial w_{21}} = (y-label)\times a_{11}\times \frac{\partial ReLU(w_{21}a_{11}+b_2)}{\partial w_{21}a_{11}+b_2} ∂w21∂J(w21,b)=∂y∂J∂a21∂y∂w21∂a21=∂y∂21(y−label)2∂a21∂a21∂w21∂ReLU(w21a11+b2)=(y−label)∂w21a11+b2∂ReLU(w21a11+b2)∂w21∂w21a11+b2=(y−label)×a11×∂w21a11+b2∂ReLU(w21a11+b2)
求J对b_2的梯度
∂J(w21,b2)∂b2=∂J(w21,b2)∂y∂y∂a21∂a21∂b2=∂12(y−label)2∂y∂y∂a21∂ReLU(w21a11+b2)∂w21a11+b2∂w21a11+b2∂b2 \frac{\partial J(w_{21},b_2)}{\partial b_2} = \frac{\partial J(w_{21},b_2)}{\partial y}\frac{\partial y}{\partial a_{21}}\frac{\partial a_{21}}{\partial b_2} = \frac{\partial \frac{1}{2}(y-label)^2}{\partial y}\frac{\partial y}{\partial a_{21}}\frac{\partial ReLU(w_{21}a_{11}+b_2)}{\partial w_{21}a_{11}+b_2}\frac{\partial w_{21}a_{11}+b_2}{\partial b_2} ∂b2∂J(w21,b2)=∂y∂J(w21,b2)∂a21∂y∂b2∂a21=∂y∂21(y−label)2∂a21∂y∂w21a11+b2∂ReLU(w21a11+b2)∂b2∂w21a11+b2
求J对w_11的梯度
∂J(w11,b)∂w11=∂J∂y∂y∂a21∂a21∂a11∂a11∂w11=(y−label)×1×∂ReLU(w21a11+b2)∂w21a11+b2×∂w21a11+b2∂a11×∂σ(w11x1+b1)∂w11x1+b1×∂w11x1+b1∂w11 \frac{\partial J(w_{11},b)}{\partial w_{11}} = \frac{\partial J}{\partial y}\frac{\partial y}{\partial a_{21}}\frac{\partial a_{21}}{\partial a_{11}}\frac{\partial a_{11}}{\partial w_{11}} = (y-label)\times1\times\frac{\partial ReLU(w_{21}a_{11}+b_2)}{\partial w_{21}a_{11}+b_2}\times\frac{\partial w_{21}a_{11}+b_2}{\partial a_{11}}\times\frac{\partial \sigma(w_{11}x_1+b_1)}{\partial w_{11}x_1+b_1}\times\frac{\partial w_{11}x_1+b_1}{\partial w_{11}} ∂w11∂J(w11,b)=∂y∂J∂a21∂y∂a11∂a21∂w11∂a11=(y−label)×1×∂w21a11+b2∂ReLU(w21a11+b2)×∂a11∂w21a11+b2×∂w11x1+b1∂σ(w11x1+b1)×∂w11∂w11x1+b1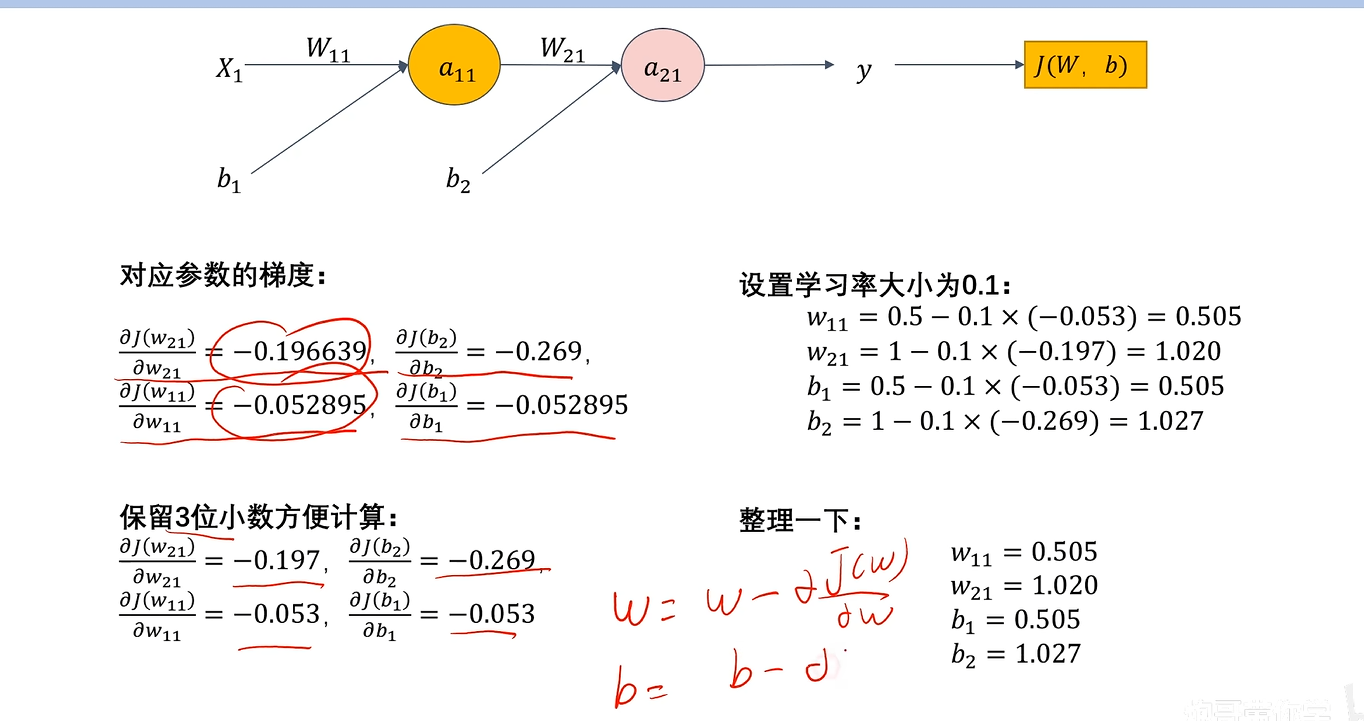
经典的梯度更新
wj=wj=α∂J∂wbj=bj=α∂J∂b w_j = w_j = \alpha\frac{\partial J}{\partial w} \\ b_j = b_j = \alpha\frac{\partial J}{\partial b} wj=wj=α∂w∂Jbj=bj=α∂b∂J
代码实现
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
# 3组2特征输入
X = np.array([
[1, 2],
[2, 3],
[4, 6],
])
# 标签
Y = np.array([
[10],
[11],
[15]
])
# 输入层大小
input_size = X.shape[1]
# 神经元个数
hidden_size = 2
# 输出层大小
output_size = Y.shape[1]
# 输入层到隐藏层的权重矩阵,input_size*hidden_size是为了让输入的每个特征都与隐藏层中每个神经元有权重连接
W1 = np.random.randn(input_size, hidden_size)
# 隐藏层到输出层的权重矩阵,hidden_size*output_size是为了让隐藏层中每个神经元都与输出层的输出有权重连接
W2 = np.random.randn(hidden_size, output_size)
# W1*X.shape=(X.shape[0],hidden_size),B1.shape=(1,hidden_size)有利于广播对齐
B1 = np.zeros((1, hidden_size))
# 输出的格式是Y.shape,B2.shape=(1,output_size)有利于广播对齐以及运算
B2 = np.zeros((1, output_size))
learning_rate = 0.1
nums_epochs = 1000
test_epochs = 1000
error_list = []
def ReLU(x):
# 将所有负值变为 0,正值保持不变
return np.maximum(0, x)
def ReLU_de(x):
# (x > 0):将列表转换为布尔列表;如果列表中元素大于0,该位置就是True;.astype(float) True->1.0 False—>0.0
return (x > 0).astype(float)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_de(x):
y = sigmoid(x)
return y * (1 - y)
def mse(Y_pred, Y):
m = len(Y_pred)
return np.sum((Y_pred - Y) ** 2) / (2 * m)
m = X.shape[0]
for i in range(nums_epochs):
# 前向传播
z = np.dot(X, W1) + B1
a1 = sigmoid(z)
# print(a1.shape)
z2 = np.dot(a1, W2) + B2
a2 = ReLU(z2)
# print(a2.shape)
# 反向传播
# mse
MSE = mse(a2, Y)
error_list.append(MSE)
# J对Y的偏导
pJpY = (a2 - Y) / m
# Y对a2的偏导
pYpa2 = 1
# a2对w2a1+b2的偏导
dR = ReLU_de(z2)
# w2a1+b2对w2的偏导
pa2pw2 = a1
# a1.shape=(3,2) (a2-Y).shape = dR.shape=(3,1),而dw2的shape要和W2相同,即(2,1)
delta2 = pJpY * pYpa2 * dR
dw2 = np.dot(pa2pw2.T, delta2)
# a2对a1的偏导
pa2pa1 = W2
# a1对w1X+b1的偏导
dS = sigmoid_de(z)
# delta*X
# (3,1) (2,1) (3,2) (3,2)
delta1 = np.dot(delta2, W2.T) * dS
dw1 = np.dot(X.T, delta1)
W1 -= learning_rate * dw1
W2 -= learning_rate * dw2
plt.plot(error_list, label="Learning curve")
plt.xlabel("Iteration")
plt.ylabel("Loss")
plt.legend()
plt.grid(True)
plt.show()
z1_test = np.dot(X, W1) + B1
a1_test = sigmoid(z1_test)
z2_test = np.dot(a1_test, W2) + B2
a2_test = ReLU(z2_test)
print("预测结果\n", a2_test)
print("实际结果\n", Y)
学习曲线
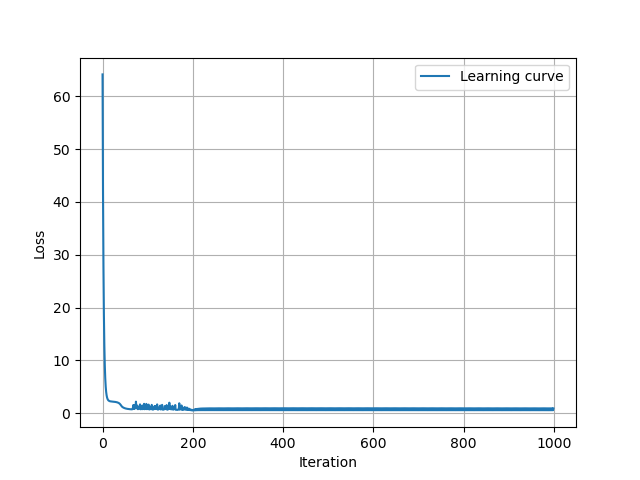
输出结果
预测结果
[[ 9.22571926]
[11.27514153]
[13.36276318]]
实际结果
[[10]
[11]
[15]]
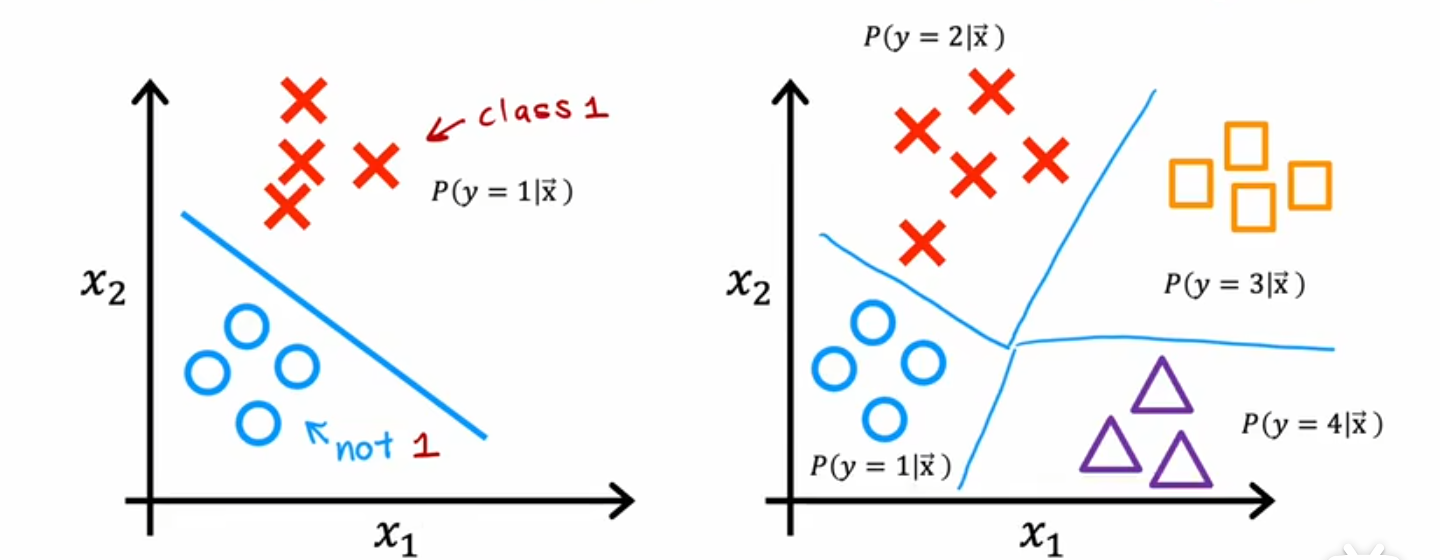
多类
目标标签超过两个的分类任务,输出标签可以是两个中的一个,也可以是多个类别中的任意一个类别
与二分类的图像对比
SoftMax的损失函数
逻辑回归中:交叉熵损失函数:
J(w)=−1m∑i=1m(yilog(σ(wTxi+b))+(1−yi)log(1−σ(wTxi+b))) J(w)= -\frac{1}{m}\sum_{i=1}^m(y_ilog(\sigma(w^Tx_i+b))+(1-y_i)log(1-\sigma(w^Tx_i+b))) J(w)=−m1i=1∑m(yilog(σ(wTxi+b))+(1−yi)log(1−σ(wTxi+b)))
将逻辑回归中推出的交叉熵损失函数进行推广以应用到SoftMax上
P(y∣X)=σ(wTxi+b)y[1−σ(wTxi+b)](1−y)a1=P(1∣X)=σ(wTxi+b)a2=1−a1=P(0∣X)=1−σ(wTxi+b)loss=−ylog(a1)−(1−y)log(1−a1)1是真实类别时:loss=−log(a1)0是真实类别时:loss=−log(a2)我们使用一种叫做one−hot编码的方式,将y,(1−y)统一成0或1,只有真实的标签才是1,此时我们可以将公式变为:loss=−∑i=1myilog(ai)J(w,b)=−1m∑i=1myilog(ai) P(y|X) = \sigma(w^Tx_i+b)^y[1-\sigma(w^Tx_i+b)]^{(1-y)}\\ a_1=P(1|X)=\sigma(w^Tx_i+b) \\ a_2 = 1-a_1= P(0|X) = 1-\sigma(w^Tx_i+b) \\ loss = -ylog(a_1)-(1-y)log(1-a_1) \\ 1是真实类别时:loss =-log(a1)\\ 0是真实类别时:loss =-log(a2)\\ 我们使用一种叫做one-hot编码的方式,将y,(1-y)统一成0或1,只有真实的标签才是1,此时我们可以将公式变为: \\ loss = -\sum_{i=1}^{m}y_ilog(a_i) \\ J(w,b) = -\frac{1}{m}\sum_{i=1}^{m}y_ilog(a_i) P(y∣X)=σ(wTxi+b)y[1−σ(wTxi+b)](1−y)a1=P(1∣X)=σ(wTxi+b)a2=1−a1=P(0∣X)=1−σ(wTxi+b)loss=−ylog(a1)−(1−y)log(1−a1)1是真实类别时:loss=−log(a1)0是真实类别时:loss=−log(a2)我们使用一种叫做one−hot编码的方式,将y,(1−y)统一成0或1,只有真实的标签才是1,此时我们可以将公式变为:loss=−i=1∑myilog(ai)J(w,b)=−m1i=1∑myilog(ai)
one-hot编码
one-hot编码是用于将**类别型数据(类别标签等)**转换为二进制向量的编码方法;对于有N个类别的分类任务,每个类别会被表示为一个长度为N的二进制向量,只有一个位置为1,其他位置都为0
在分类任务中,真实类别是第i类,则yj={1ifj=i,0其他 在分类任务中,真实类别是第i类,则 \\ y_j = \begin{cases} 1&if&j=i,\\ 0&其他 \end{cases} 在分类任务中,真实类别是第i类,则yj={10if其他j=i,
比如2分类中,我们假设y=1是正例,y=2是反例
二进制向量=(1,0)loss=−∑i=1Nyilog(ai)=−log(a1)+0×(−log(a2)) 二进制向量=(1,0)\\ loss = -\sum_{i=1}^{N}y_ilog(a_i) = -log(a_1)+0\times(-log(a_2)) 二进制向量=(1,0)loss=−i=1∑Nyilog(ai)=−log(a1)+0×(−log(a2))
SoftMax的损失函数
1.使用one-hot编码+交叉熵简化形式
loss=−∑i=1myilog(ai)loss=−log(aj),当y=j其中yi是one−hot编码后二进制向量第i个元素的值;aj是SoftMax计算得到的概率 loss = -\sum_{i=1}^{m}y_ilog(a_i)\\ loss = -log(a_j),当y=j\\ 其中y_i是one-hot编码后二进制向量第i个元素的值;a_j是SoftMax计算得到的概率 loss=−i=1∑myilog(ai)loss=−log(aj),当y=j其中yi是one−hot编码后二进制向量第i个元素的值;aj是SoftMax计算得到的概率
分析:对于损失loss,每个训练样例的y都只能取一个值;当a_j越小,-log(a_j)的值会越大,因此模型会激励a_j变大,尽可能接近1
SoftMax实现输出层
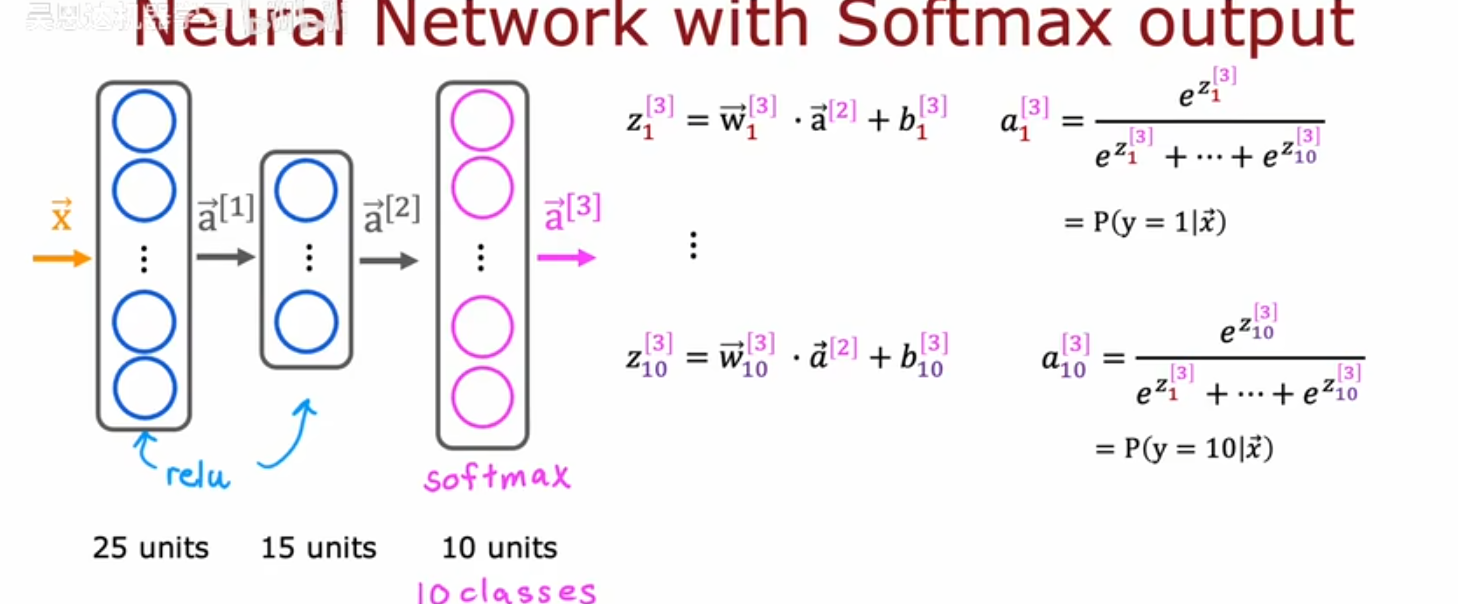
zj[l]=wj[l]⃗a⃗+bj[i]aj[l]=ezj[l]∑i=1unitseei[l]units:神经元数 z_j^{[l]} = \vec{w_j^{[l]}}\vec{a}+b_j^{[i]} \\ a_j^{[l]} = \frac{e^{z_j^{[l]}}}{\sum_{i=1}^{units}e^{e_i^{[l]}}}\\ units:神经元数 zj[l]=wj[l]a+bj[i]aj[l]=∑i=1unitseei[l]ezj[l]units:神经元数
减少数字舍入误差
在计算机中,存储浮点数的精度是有限的
比如:

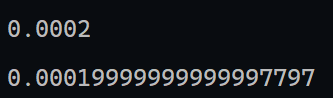
发现在数学上计算相等的两个算式,在代码中却出现了运行结果不相等
tensorflow可以对这种情况做出优化
逻辑回归例子
以逻辑回归的loss值为例,我们看看数学上等价的两个公式
a=g(w⃗x⃗+b)=g(z)=11+e−zloss=−∑i=1m(ylog(a)+(1−y)log(1−a)) a = g(\vec{w}\vec{x}+b) = g(z) = \frac{1}{1+e^{-z}} \\ loss = - \sum_{i=1}^{m}(ylog(a)+(1-y)log(1-a))\\ a=g(wx+b)=g(z)=1+e−z1loss=−i=1∑m(ylog(a)+(1−y)log(1−a))
对应的代码
model1 = Sequential([
Dense(units=10, activation=relu),
Dense(units=5, activation=relu),
Dense(units=1, activation=sigmoid),
])
# 将模型损失值用激活函数计算后,再传入损失函数中计算
model1.compile(loss=BinaryCrossentropy())
loss=−∑i=1m(ylog(11+e−z)+(1−y)log(1−11+e−z)) loss = -\sum_{i=1}^{m}(ylog(\frac{1}{1+e^{-z}})+(1-y)log(1-\frac{1}{1+e^{-z}})) loss=−i=1∑m(ylog(1+e−z1)+(1−y)log(1−1+e−z1))
model2 = Sequential([
Dense(units=10, activation=relu),
Dense(units=5, activation=relu),
Dense(units=1, activation=linear), # 直接输出线性拟合的结果,在计算损失函数处再进行激活
])
# 将BinaryCrossentropy当作方法调用(使用了python中的__call__,类似于PHP的__invoke)
# logits是模型输出的原始输出值(未经过激活函数),from_logits=True会将原始输出直接扔进损失函数中再应用激活函数,最终计算出损失
model2.compile(loss=BinaryCrossentropy(from_logits=True))
model2.fit(X, Y, epochs=500)
# 前向传播值
logits = model2(X)
predict = tf.nn.sigmoid(logits)
整体对比代码
import numpy as np
from keras.activations import relu, sigmoid, linear
from keras.losses import BinaryCrossentropy
from tensorflow.keras.layers import Dense
from tensorflow.keras import Sequential
X = np.array([
[1., 2.],
[3., 4.],
[5., 6.],
])
# 逻辑回归2分类任务
Y = np.array([0, 1, 1])
model1 = Sequential([
Dense(units=10, activation=relu),
Dense(units=5, activation=relu),
Dense(units=1, activation=sigmoid),
])
# 将模型损失值用激活函数计算后,再传入损失函数中计算
model1.compile(loss=BinaryCrossentropy())
model1.fit(X, Y, epochs=500)
model2 = Sequential([
Dense(units=10, activation=relu),
Dense(units=5, activation=relu),
Dense(units=1, activation=linear), # 直接输出线性拟合的结果,在计算损失函数处再进行激活
])
# 将BinaryCrossentropy当作方法调用(使用了python中的__call__,类似于PHP的__invoke)
# logits是模型输出的原始输出值(未经过激活函数),from_logits=True会将原始输出直接扔进损失函数中再应用激活函数,最终计算出损失
model2.compile(loss=BinaryCrossentropy(from_logits=True))
model2.fit(X, Y, epochs=500)
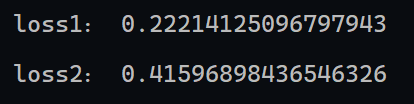
# 使用evaluate获得编译时设置的loss模型的计算值
loss1 = model1.evaluate(X, Y)
loss2 = model2.evaluate(X, Y)
print("loss1:", loss1)
print("loss2:", loss2)
运行结果
python知识:
-
__call__:将对象实例作为方法调用,与PHP的__invoke很类似class test: def __init__(self): print("__init") def __call__(self, X): print(f"call:{X}") t = test() t(1)
<?php
class test{
public $a;
public function __invoke()
{
echo "__invoke";
}
}
$t = new test();
$t();

对SoftMax进行优化
原本的公式
a⃗=(a1,a2,…,a10)=g(z1,z2,…,z10)Loss=L(a⃗,y)={−log(a1)ify=1,⋮−log(a10)ify=10 \vec{a} =(a_1,a_2,\dots,a_{10}) = g(z_1,z_2,\dots,z_{10}) \\ Loss = L(\vec{a},y) = \begin{cases} -log(a_1)&if&y=1,\\ \vdots\\ -log(a_{10})&if&y=10\\ \end{cases} a=(a1,a2,…,a10)=g(z1,z2,…,z10)Loss=L(a,y)=⎩
⎨
⎧−log(a1)⋮−log(a10)ifify=1,y=10
model1 = Sequential([
Dense(units=10, activation=relu),
Dense(units=5, activation=relu),
Dense(units=10, activation=softmax),
])
# 将模型损失值用激活函数计算后,再传入损失函数中计算
# 使用稀疏类别交叉熵SparseCategoricalCrossentropy
model1.compile(loss=SparseCategoricalCrossentropy())
model1.fit(X, Y, epochs=500)
# 获得前向结果值
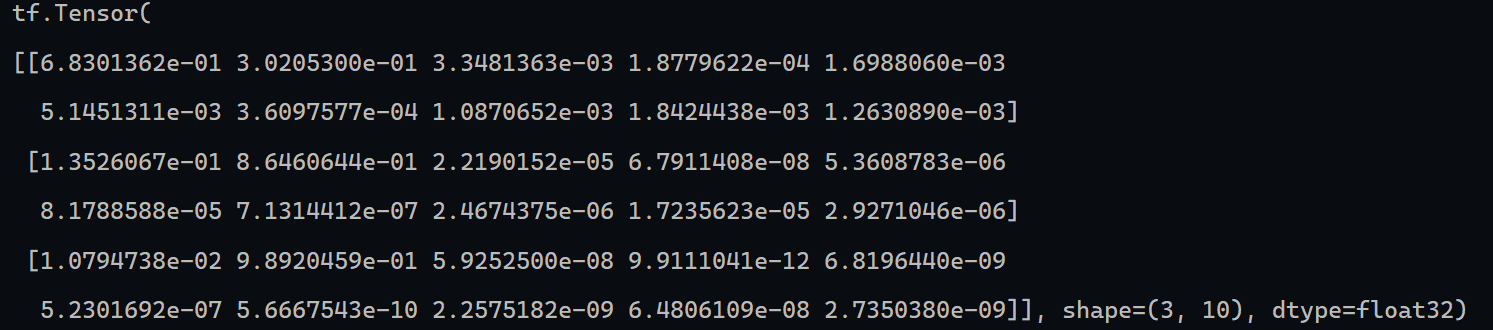
predict1 = model1(X)
print(predict1)
将激活函数这一步直接放在计算损失中
Loss=L(a⃗,y)={−log(ez1ez1+ez2+⋯+ez10)ify=1,⋮−log(ez10ez1+ez2+⋯+ez10)ify=10 Loss = L(\vec{a},y) = \begin{cases} -log(\frac{e^{z_1}}{e^{z_1}+e^{z_2}+\dots+e^{z_{10}}})&if&y=1,\\ \vdots\\ -log(\frac{e^{z_{10}}}{e^{z_1}+e^{z_2}+\dots+e^{z_{10}}})&if&y=10\\ \end{cases} Loss=L(a,y)=⎩
⎨
⎧−log(ez1+ez2+⋯+ez10ez1)⋮−log(ez1+ez2+⋯+ez10ez10)ifify=1,y=10
model2 = Sequential([
Dense(units=10, activation=relu),
Dense(units=5, activation=relu),
Dense(units=10, activation=linear), # 直接输出线性拟合的结果,在计算损失函数处再进行激活
])
# 将SparseCategoricalCrossentropy当作方法调用
# logits是模型输出的原始输出值(未经过激活函数),from_logits=True会将原始输出直接扔进损失函数中再应用激活函数,最终计算出损失
model2.compile(loss=SparseCategoricalCrossentropy(from_logits=True))
model2.fit(X, Y, epochs=500)
#预测
# 获取最后一层输出的向量,输出z1->z10而不是a1->a10
# 将model当作方法获得前向传播结果与.predict()有什么区别?:model(X):X:tf.Tensor return:tf.Tensor .predict(X): X:numpy,tensor,dataset return:numpy.ndarray
logits = model2(X)
# 获取最终的概率分布
predict = tf.nn.softmax(logits)
什么是稀疏交叉熵损失函数(SparseCategoricalCrossentropy)?
- 适用于这样的多分类任务:标签是整数(表示编号),模型输出是概率分布(像softmax这样的输出)
损失函数
L(Py)=−log(Py)Py:真实标签对应的案例比如,标签向量是[0,1,2],模型输出的概率分布是[0.6,0.2,0.2],真实标签是0,那损失函数就是−log(0.6) L(P_y) = -log(P_y) \\ P_y:真实标签对应的案例 \\ 比如,标签向量是[0,1,2],模型输出的概率分布是[0.6,0.2,0.2],真实标签是0,那损失函数就是-log(0.6) L(Py)=−log(Py)Py:真实标签对应的案例比如,标签向量是[0,1,2],模型输出的概率分布是[0.6,0.2,0.2],真实标签是0,那损失函数就是−log(0.6)
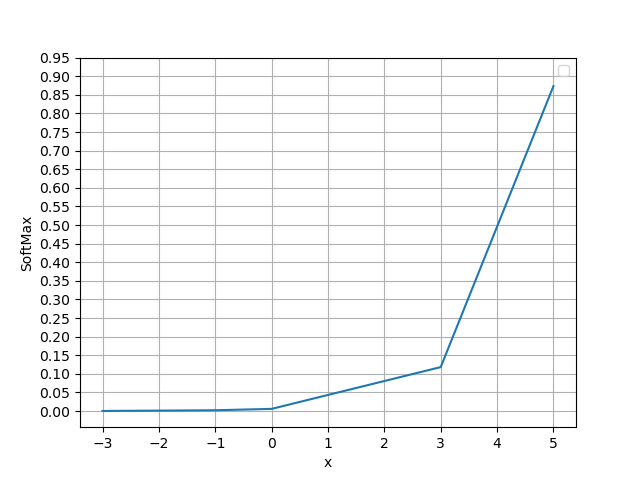
SoftMax的一个特点就是使输出两极化,体现为
- 正样本趋近1,负样本趋近0
- 样本绝对值越大,两极化越明显
import numpy as np
import matplotlib.pyplot as plt
def softmax(x):
exp_x = np.exp(x)
sum = np.sum(exp_x)
return exp_x / sum
X = np.array([-3, -1, 0, 3, 5])
Y = softmax(X)
# [ ... for val in Y ]这个操作表示对Y中元素进行...操作后放入新列表
print([f"{val:.4f}" for val in Y])
fig, ax = plt.subplots()
ax.plot(X, Y)
# 设置坐标轴精度
ax.yaxis.set_ticks(np.arange(0, 1, 0.05))
plt.xlabel("x")
plt.ylabel("SoftMax")
plt.legend()
plt.grid(True)
plt.show()
输出结果
['0.0003', '0.0022', '0.0059', '0.1182', '0.8734']
图像
存在的问题
- 对于很大的输入(大到->+∞),分子的会变得非常非常大,大到变成inf,而分母同样也会变成inf,softmax计算出的值就不确定了(inf / inf 最终结果是nan),这就是上溢
- 对于很小的输入(小到->-∞),分子->0,导致最终的结果被四舍五入为0,这就是下溢
优化1
思路:控制输入向量中x_i的大小;在进行幂指数运算时先减去向量中的最大值,这样一来,输入x_i-max(x)的大小范围就在(-∞,0]
SoftMax(xi)=exi−xamx∑j=1mexj SoftMax(x_i) = \frac{e^{x_i-x_{amx}}}{\sum_{j=1}^{m}e^{x_j}} SoftMax(xi)=∑j=1mexjexi−xamx
输入特征X
X = np.array([-3, -1, 0, 3, 1000])
使用原始的softmax(上文的softmax),输出结果
exp_x [ 0.04978707 0.36787944 1. 20.08553692 inf]
sum inf
['0.0000', '0.0000', '0.0000', '0.0000', 'nan']
使用优化后的softmax:
def softmax(x):
# np.max用于获取列表中最大值
# 与np.maximum区别:np.maximum用于比较两个列表X,Y,返回列表是X,Y中较大的那个元素,形状不同会通过numpy的广播机制进行对齐,无法对齐就会报错
exp_x = np.exp(x - np.max(x))
print("exp_x", exp_x)
sum = np.sum(exp_x)
print("sum", sum)
return exp_x / sum
运行结果
exp_x [0. 0. 0. 0. 1.]
sum 1.0
['0.0000', '0.0000', '0.0000', '0.0000', '1.0000']
这个优化后的softmax解决了上溢问题,但是并没有解决下溢的问题,如果最大值太大,会导致有很多结果丢失精度变为0
优化2
这个算法被称为log_softmax,将上面优化1的公式取对数
SoftMax(xi)=logexi−xmax∑j=1mexj=log(exi−xmax)−log(∑j=1mexj)=xi−xmax−log(∑i=1mexj) SoftMax(x_i) = log\frac{e^{x_i-x_{max}}}{\sum_{j=1}^{m}e^{x_j}} = log(e^{x_i-x_{max}})-log(\sum_{j=1}^{m}e^{x_j})=x_i-x_{max}-log(\sum_{i=1}^{m}e^{x_j}) SoftMax(xi)=log∑j=1mexjexi−xmax=log(exi−xmax)−log(j=1∑mexj)=xi−xmax−log(i=1∑mexj)
多标签分类问题
是一种与每个图像相关联的,有多个输出标签的分类问题
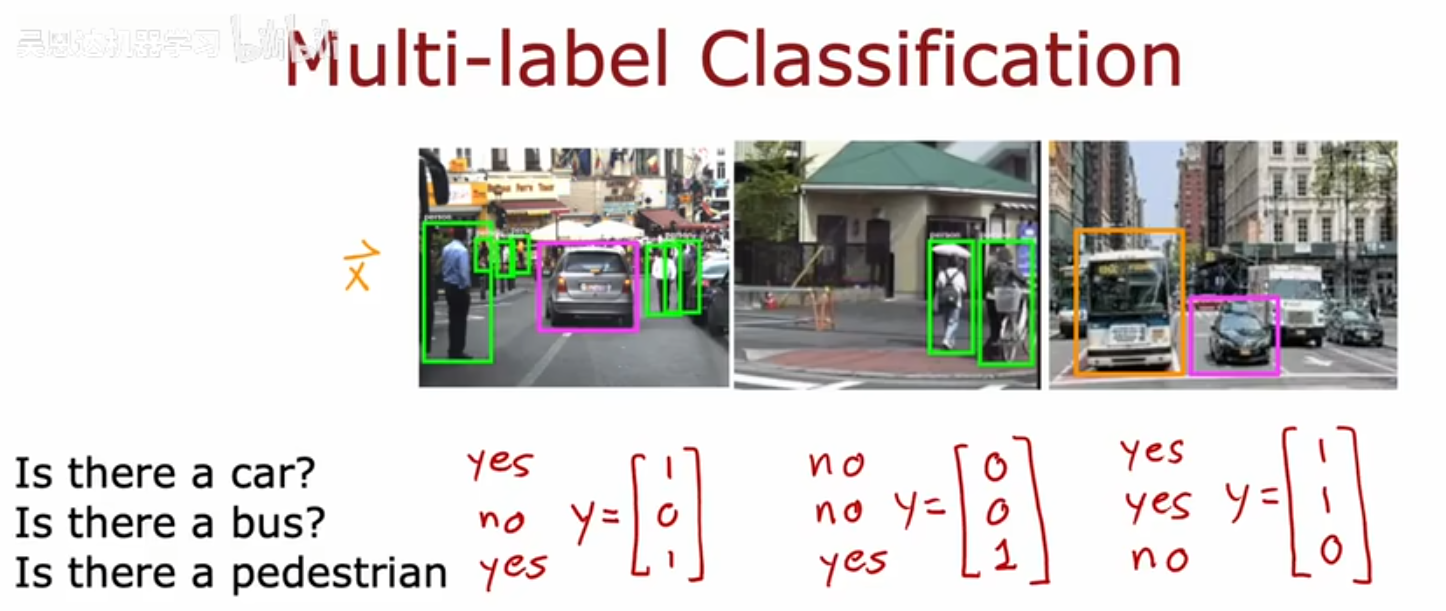
区别:输出标签向量y中不只有一个真实类别;多分类问题,即使有多个输入特征,最终输出的真实类别也只有一个
也就是说,输出向量中元素是不互斥的,可以不只有一个1
如何构建神经网络
方法1:把三个标签分类分别当作三个神经网络(不推荐)

方法2:训练一个神经网络同时检测三种情况
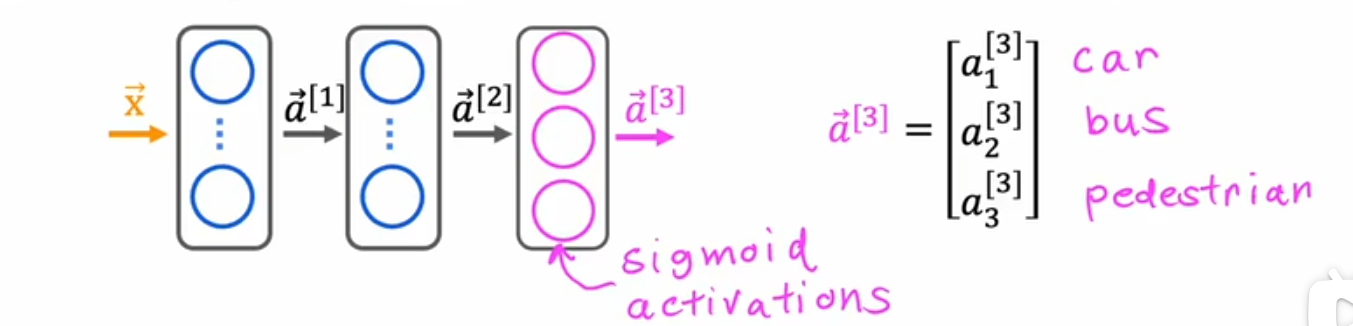
可以视作三个二分类问题,因此激活函数可以使用sigmoid
高级优化方法
Adam算法(自适应向量估计)
自动调整学习率以实现更高效地梯度下降;adam算法为模型的每个参数使用不同的学习率
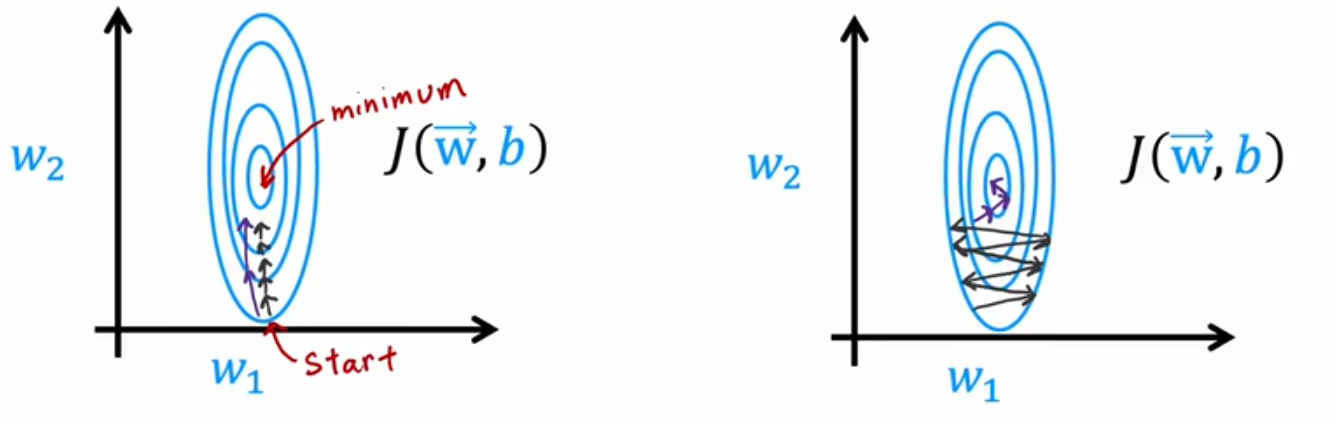
直观理解:如果参数wj和b似乎一直在大致相同的方向上移动,那么学习率太小,adam算法会增大该参数的学习率;如果一个参数来回震荡,那么学习率太大,adam算法会减小该参数的学习率
在代码中使用
编译模型时指定优化项
# 定义密集层
model = Sequential([
Dense(units=25, activation=sigmoid),
Dense(units=15, activation=sigmoid),
Dense(units=5, activation=linear)
])
# 编译
model.compile(
loss=SparseCategoricalCrossentropy(from_logits=True),
# 指定优化器为adam,初始学习率为0.001
optimizer=keras.optimizers.Adam(learning_rate=1e-3)
)
优点:可以自动调整学习率,让算法整体更具有稳健性(鲁棒性)

GitCode 天启AI是一款由 GitCode 团队打造的智能助手,基于先进的LLM(大语言模型)与多智能体 Agent 技术构建,致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话,还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力,真正做到“一句话,让 Al帮你完成复杂任务”。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容










所有评论(0)