💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

一、引言

二、无人机动力学模型

三、MPC模型预测控制

1. 预测模型

2. 成本函数

3. 优化求解

4. 控制输入实施与反馈

四、PID控制器

五、ode15s求解器

六、综合应用与仿真

七、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

本代码求解方案包含以下几个方面：

Use Simulink with ode45 solver
Use ode15s solver 
Use 'sqp' solver (Sequential Quadratic Programming)
Define MPC Parameters for Altitude & x-y Controllers

以下是关于基于MPC（模型预测控制）、PID（比例-积分-微分控制器）、以及ode15s（MATLAB中的常微分方程求解器）的无人机开发模型预测控制的研究文档概要：

一、引言

无人机（UAV）在航拍、货物配送、搜索救援等领域的应用日益广泛，对其自主导航和轨迹跟踪能力提出了更高要求。模型预测控制（MPC）作为一种基于模型的控制技术，通过预测未来状态并优化控制输入来实现对复杂系统的控制，非常适合用于无人机的控制系统中。本文旨在探讨结合MPC、PID控制器以及ode15s求解器在无人机模型预测控制中的应用。

二、无人机动力学模型

首先，需要建立一个准确的无人机动力学模型，该模型应能够描述无人机的平移和旋转运动。这通常包括无人机的质量、惯性矩、推力、升力等参数。常用的运动学模型包括四旋翼无人机的六自由度（6-DOF）模型，描述位置、速度、加速度、姿态角等参数。

三、MPC模型预测控制

1. 预测模型

基于无人机动力学模型，构建未来N步的预测模型，用于预测无人机在不同控制输入下的状态变化。这通常涉及到对系统状态的在线计算和更新。

2. 成本函数

定义一个成本函数，用于衡量预测状态与期望状态之间的偏差。成本函数应考虑到无人机的各种约束条件，如最大速度、最大俯仰角等。

3. 优化求解

在给定的预测范围内，使用优化算法（如二次规划、线性规划等）找到控制输入序列，以最小化成本函数。优化求解过程应考虑到无人机的实时性和计算资源限制。MATLAB中的优化工具箱，如fmincon，可以用于此目的。

4. 控制输入实施与反馈

将优化后的第一个控制输入应用到无人机中，实现实时控制。使用传感器数据（如GPS、陀螺仪、加速度计等）实时估计无人机的当前状态，并将状态信息反馈给MPC控制器，以便进行下一轮预测和优化。

四、PID控制器

PID控制器是一种经典的控制方法，通过调整比例、积分和微分增益来控制系统输出。在无人机控制中，PID控制器可以用于辅助MPC控制器，提供稳定的控制输入，特别是在系统动态变化较快的情况下。

五、ode15s求解器

ode15s是MATLAB中的一个常微分方程求解器，适用于刚性方程组的求解。在无人机动力学模型中，可能涉及到一些刚性动力学方程，此时可以使用ode15s进行求解，以获得更准确的系统状态。

六、综合应用与仿真

结合MPC、PID控制器和ode15s求解器，构建无人机模型预测控制系统的综合框架。使用MATLAB/Simulink等仿真工具进行仿真验证，评估系统的性能，包括轨迹跟踪精度、鲁棒性和实时性等。

七、结论与展望

本文通过对基于MPC、PID控制器和ode15s求解器的无人机模型预测控制进行研究，提出了一种综合的控制策略。仿真结果表明，该策略能够显著提高无人机的自主飞行能力和轨迹跟踪精度。未来工作可以进一步探索更先进的优化算法、更精确的动力学模型以及更高效的计算方法，以进一步提升无人机控制系统的性能。

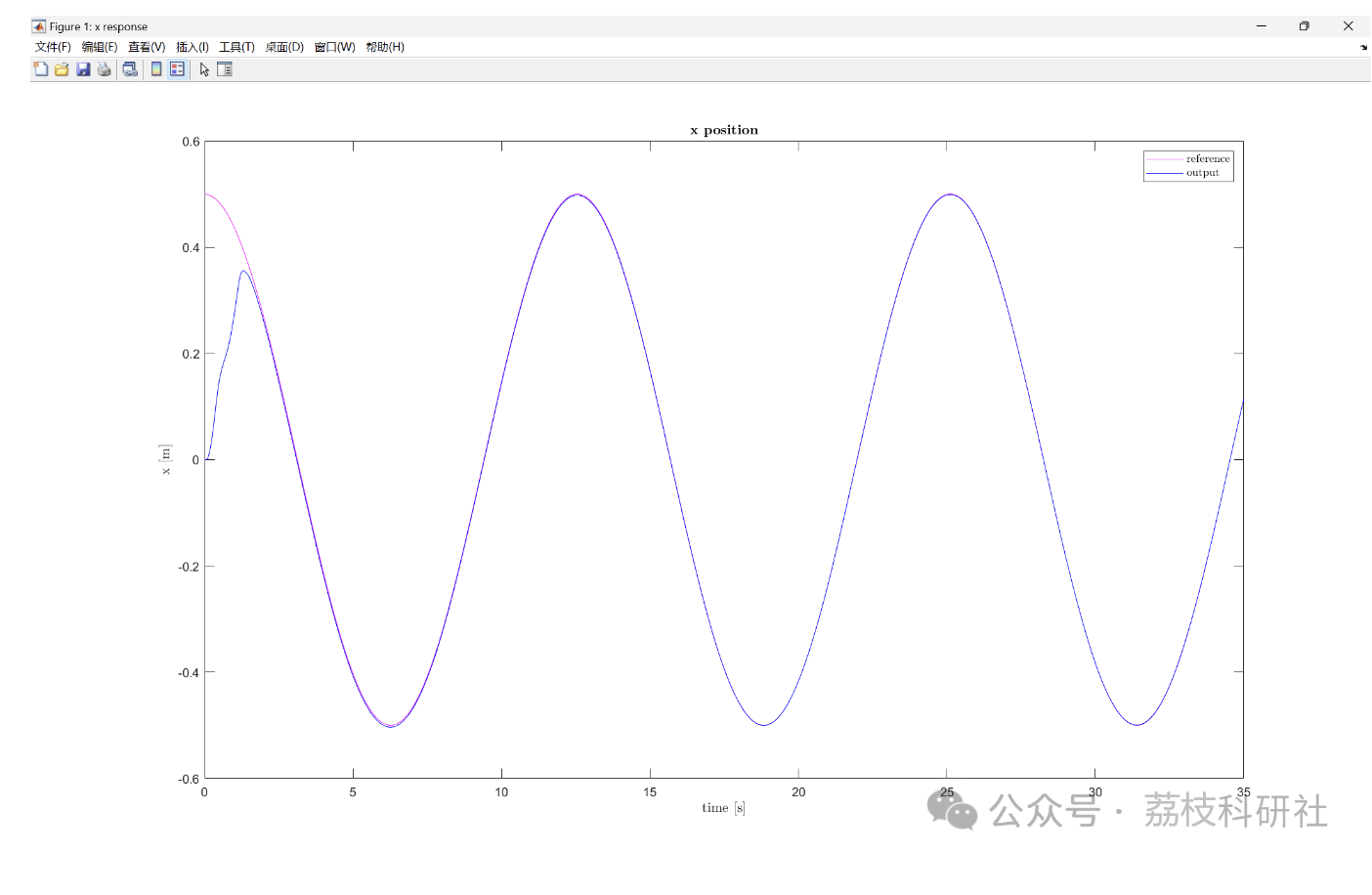
📚2 运行结果

主函数部分代码：

% Model Predictive Controller using Linear Adaptive Prediction model
% MATLAB main script
%
​
%% Clear Workspace & Command Window
close all %
 Optionalclc
clear 
format long
​
%% Fix MATLAB Path
path = pwd();
addpath(genpath(path));
​
%
% Load constant data 
for
 the modelsetSimulationSettings()
​
%% Create quadcopter struct (quad) & Load basic fields
quadStructBasics()
​
%
% Define MPC Parameters 
for
 Altitude & x-y ControllerssetMPCSettings()
​
%% Define options for Optimizer
​
%
 Use 
'sqp'
 solver (Sequential Quadratic Programming)options = optimoptions('fmincon','Display','None','Algorithm','sqp');
​
%% Define initial conditions for ftPrev,xPrev,yPrev,DftPrev,DuxPrev,DuyPrev
​
ftPrev = 0;                   %
 Previous Total Thrust DftPrev = zeros(1,mpcParamsAlt.Nc);
​
uxPrev = 0;                   % Previous ux
uyPrev = 0;                   % Previous uy
​
DuxyPrev = zeros(mpcParamsXY.Nc,2);
​
initConditions = zeros(1,12); % Initial conditions for system states [phi theta psi p q r u v w x y z] 
​
% Save initial conditions in struct
simOut.states = initConditions;
​
%% Initialize system states
​
%
 --- Earth Frame --- %%---------------------%
​
% Linear Positions 
x = [];
y = [];
z = [];
​
% Angular Positions 
phi   =  [];
theta =  [];
psi   =  [];
​
​
% ---- Body Frame --- %
%---------------------%
​
% Linear Velocities 
u = [];
v = [];
w = [];
​
% Angular Velocities 
p = [];
q = [];
r = [];
​
%-------------------------------------------%
​
% Initialize Objective Functions Evaluations
Jz = [];
Jxy = [];
​
% Initialize reference angles
phi_ref   = [];
theta_ref = [];
psi_ref = [];
​
%% PID Settings
setPIDSettings()
​
%
% Main Loop​
fprintf("\nSimulation started\n")
​
% Yaw Reference Vector
psi_ref = zeros(length(1:(duration/Ts)+1),1);
​
for k = 1:(duration/Ts)+1
​
    %% Generate reference sub-vector for current time step
​
    %
 Altitude z    refVectorAlt = getReferenceSignal(Ts,(k+1:k+mpcParamsAlt.Np),'Signal','ramp_z');
​
    % x
    refVectorX = getReferenceSignal(Ts,(k+1:k+mpcParamsXY.Np),'Signal','cos_x');
    % y
    refVectorY = getReferenceSignal(Ts,(k+1:k+mpcParamsXY.Np),'Signal','sin_y');
​
    % x'
    refVectorXDot= getReferenceSignal(Ts,(k+1:k+mpcParamsXY.Np),'
Signal
','
cos_xDot
');
    % y'
    refVectorYDot = getReferenceSignal(Ts,(k+1:k+mpcParamsXY.Np),'Signal','sin_yDot');
​
    %% Print current step k 
    progress = k/((duration/Ts)+1)*100;
    fprintf("\nSimulation Time Step %
d - 
Progress:
 %.
1
f
%%", k, progress)
​
    z = [z; simOut.states(end,end)];
    
    %
 Update x,y    x = [x; simOut.states(end,end-2)];
    y = [y; simOut.states(end,end-1)];
    
    % Update phi,theta,psi
    phi = [phi; simOut.states(end,1)]; 
    theta = [theta; simOut.states(end,2)];
    psi = [psi; simOut.states(end,3)];

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]史宝岱,徐艳召,崔俊杰,等.基于卷积神经网络的无人机图像自动识别算法[J].信息工程大学学报,2023,24(05):526-532.

[2]谢睿.基于改进MPC的自动驾驶车辆轨迹跟踪控制研究[D].山东交通学院,2024.DOI:10.27864/d.cnki.gsjtd.2024.000181.

部分理论引用网络文献，若有侵权联系博主删除

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取