解码⽅法（medium）

题⽬链接：91. 解码⽅法

题⽬描述：

⼀条包含字⺟ A-Z 的消息通过以下映射进⾏了 编码 ：
‘A’ -> “1”
‘B’ -> “2”
…
‘Z’ -> “26”
要 解码 已编码的消息，所有数字必须基于上述映射的⽅法，反向映射回字⺟（可能有多种⽅法）。
例如，“11106” 可以映射为：
• “AAJF” ，将消息分组为 (1 1 10 6)
• “KJF” ，将消息分组为 (11 10 6)
注意，消息不能分组为 (1 11 06) ，因为 “06” 不能映射为 “F” ，这是由于 “6” 和 “06” 在映射中并不等价。
给你⼀个只含数字的 ⾮空 字符串 s ，请计算并返回 解码 ⽅法的 总数 。
题⽬数据保证答案肯定是⼀个 32 位 的整数。
⽰例 1：
输⼊：s = “12”
输出：2
解释：
它可以解码为 “AB”（1 2）或者 “L”（12）。
⽰例 2：
输⼊：s = “226”
输出：3
解释：
它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。

解法（动态规划）：

算法思路：

类似于斐波那契数列~
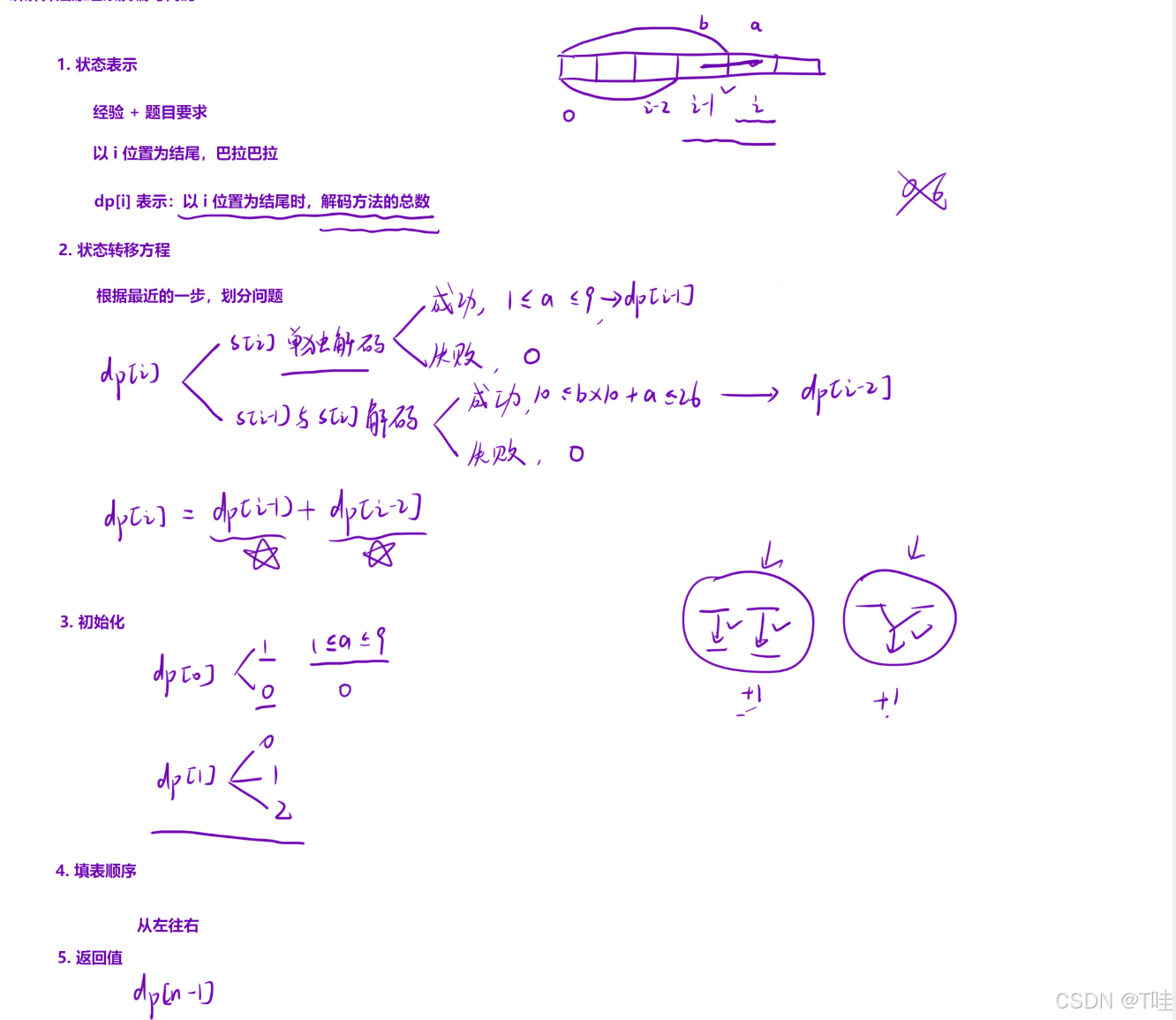
1.状态表⽰：
根据以往的经验，对于⼤多数线性 dp ，我们经验上都是「以某个位置结束或者开始」做⽂章，这⾥我们继续尝试「⽤ i 位置为结尾」结合「题⽬要求」来定义状态表⽰。
dp[i] 表⽰：字符串中 [0，i] 区间上，⼀共有多少种编码⽅法。

2.状态转移⽅程：
定义好状态表⽰，我们就可以分析 i 位置的 dp 值，如何由「前⾯」或者「后⾯」的信息推导出来。

• 关于 i 位置的编码状况，可以分为下⾯两种情况：
  i. 让 i 位置上的数单独解码成⼀个字⺟；
  ii. 让 i 位置上的数与 i - 1 位置上的数结合，解码成⼀个字⺟。

就上⾯的两种解码情况，继续分析：

• ◦ 让 i 位置上的数单独解码成⼀个字⺟，就存在「解码成功」和「解码失败」两种情况：
  i. 解码成功：当 i 位置上的数在 [1, 9] 之间的时候，说明 i 位置上的数是可以单独解码的，那么此时 [, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅法。因为 [0, i - 1] 区间上的所有解码结果，后⾯填上⼀个 i 位置解码后的字⺟就可以了。此时 dp[i] = dp[i - 1] ；
  ii. 解码失败：当 i 位置上的数是 0 的时候，说明 i 位置上的数是不能单独解码的，那么此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码，但是解码失败了，那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。

• ◦ 让 i 位置上的数与 i - 1 位置上的数结合在⼀起，解码成⼀个字⺟，也存在「解码成功」和「解码失败」两种情况：
  i. 解码成功：当结合的数在 [10, 26] 之间的时候，说明 [i - 1, i] 两个位置是可以解码成功的，那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 2 ] 区间上的解码⽅法，原因同上。此时 dp[i] = dp[i - 2] ；
  ii. 解码失败：当结合的数在 [0, 9] 和 [27 , 99] 之间的时候，说明两个位置结合后解码失败（这⾥⼀定要注意 00 01 02 03 04 … 这⼏种情况），那么此时 [0, i] 区间上的解码⽅法就不存在了，原因依旧同上。此时 dp[i] = 0 。

综上所述： dp[i] 最终的结果应该是上⾯四种情况下，解码成功的两种的累加和（因为我们关⼼的是解码⽅法，既然解码失败，就不⽤加⼊到最终结果中去），因此可以得到状态转移⽅程（ dp[i] 默认初始化为 0 ）：
i. 当 s[i] 上的数在 [1, 9] 区间上时： dp[i] += dp[i - 1] ；
ii. 当 s[i - 1] 与 s[i] 上的数结合后，在 [10, 26] 之间的时候： dp[i] += dp[i - 2] ；
如果上述两个判断都不成⽴，说明没有解码⽅法， dp[i] 就是默认值 0。

3.初始化：
⽅法⼀（直接初始化）：
由于可能要⽤到 i - 1 以及 i - 2 位置上的 dp 值，因此要先初始化「前两个位置」。
初始化 dp[0] ：
i. 当 s[0] == ‘0’ 时，没有编码⽅法，结果 dp[0] = 0 ；
ii. 当 s[0] != ‘0’ 时，能编码成功， dp[0] = 1
初始化 dp[1] ：
i. 当 s[1] 在 [1，9] 之间时，能单独编码，此时 dp[1] += dp[0] （原因同上，dp[1] 默认为 0 ）
ii. 当 s[0] 与 s[1] 结合后的数在 [10, 26] 之间时，说明在前两个字符中，⼜有⼀种编码⽅式，此时 dp[1] += 1
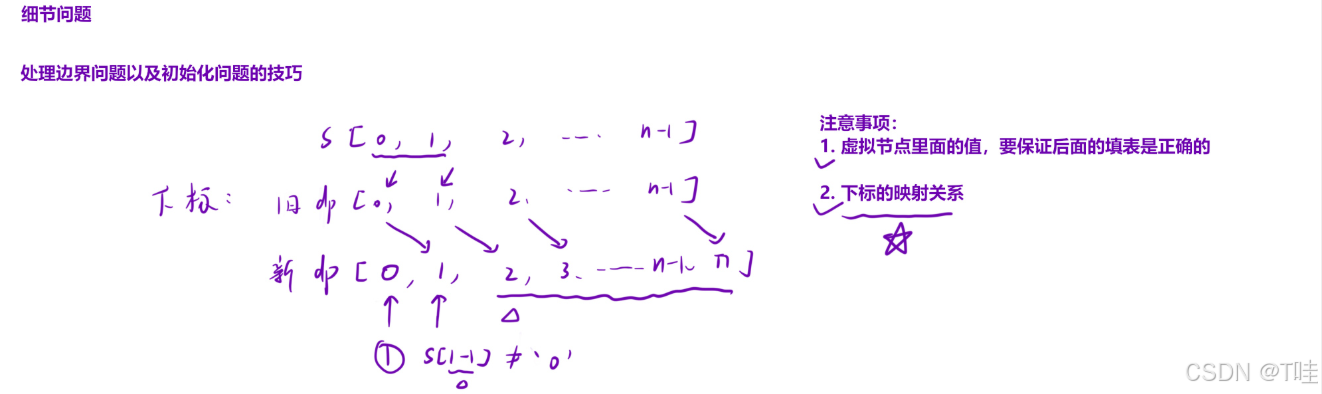
⽅法⼆（添加辅助位置初始化）：
可以在最前⾯加上⼀个辅助结点，帮助我们初始化。使⽤这种技巧要注意两个点：
i. 辅助结点⾥⾯的值要保证后续填表是正确的；
ii. 下标的映射关系

4.填表顺序：
毫⽆疑问是「从左往右」

5.返回值：
应该返回 dp[n - 1] 的值，表⽰在 [0, n - 1] 区间上的编码⽅法

算法代码：

使⽤直接初始化的⽅式解决问题：

class Solution{
 public int numDecodings(String ss) {
	 // 1. 创建 dp 表
	 // 2. 初始化
	 // 3. 填表
	 // 4. 返回值
	 int n = ss.length();
	 char[] s = ss.toCharArray();
	 int[] dp = new int[n];
	 if(s[0] != '0') dp[0] = 1; // 初始化第⼀个位置
	 if(n == 1) return dp[0]; // 处理边界情况
	 // 初始化第⼆个位置
	 if(s[1] != '0' && s[0] != '0') dp[1] += 1;
	 int t = (s[0] - '0') * 10 + s[1] - '0';
	 if(t >= 10 && t <= 26) dp[1] += 1;
	 for(int i = 2; i < n; i++){
		 // 先处理第⼀种情况
		 if(s[i] != '0') dp[i] += dp[i - 1];
		 // 处理第⼆种情况
		 int tt = (s[i - 1] - '0') * 10 + s[i] - '0';
		 if(tt >= 10 && tt <= 26) dp[i] += dp[i - 2];
	 }
	 return dp[n - 1];
 }
}

⽤添加辅助结点的⽅式初始化：

class Solution{
 public int numDecodings(String ss) {
	 // 1. 创建 dp 表
	 // 2. 初始化
	 // 3. 填表
	 // 4. 返回值
	 int n = ss.length();
	 char[] s = ss.toCharArray();
	 int[] dp = new int[n + 1];
	 dp[0] = 1; // 保证后续填表是正确的
	 if(s[1 - 1] != '0') dp[1] = 1;
	 for(int i = 2; i <= n; i++){
		 // 先处理第⼀种情况
		 if(s[i - 1] != '0') dp[i] += dp[i - 1];
		 // 处理第⼆种情况
		 int tt = (s[i - 2] - '0') * 10 + s[i - 1] - '0';
		 if(tt >= 10 && tt <= 26) dp[i] += dp[i - 2];
	 }
	 return dp[n];
 }
}