本篇延续前几篇关键技术拆解，继续系统梳理卷积神经网络（CNN）中卷积层反向传播（Backpropagation in Convolutional Layer）的数学推导、核心原理、公式、实际案例和可视化代码演示，帮助你彻底理解CNN训练的“灵魂机制”。

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

如果不了解卷积神经网络（CNN）的同学记得先回去复习爱酱讲解CNN的文章喔～

一、卷积层反向传播的核心任务

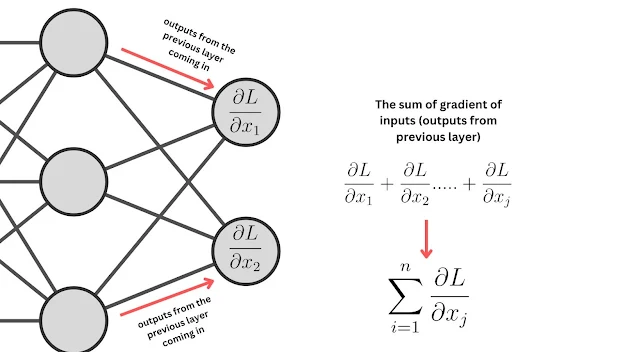
在CNN中，卷积层的反向传播主要涉及以下三类梯度的计算：

  • 对输入特征图的梯度（$\frac{\partial L}{\partial X}$）：用于将误差信号传递到前一层。

  • 对卷积核（权重）的梯度（$\frac{\partial L}{\partial W}$）：用于更新卷积核参数。

  • 对偏置的梯度（$\frac{\partial L}{\partial b}$）：用于更新偏置参数。

二、卷积层梯度推导的数学表达

1. 前向传播公式

设输入特征图为 $X$，卷积核为 $W$，偏置为 $b$，输出特征图为 $Y$，则前向传播为：

Y_{i,j} = \sum_{m=1}^{k} \sum_{n=1}^{k} W_{m,n} \cdot X_{i+m-1,\, j+n-1} + b

2. 反向传播核心公式

（1）对卷积核的梯度（Weight Gradient）

\frac{\partial L}{\partial W_{m,n}} = \sum_{i,j} \frac{\partial L}{\partial Y_{i,j}} \cdot X_{i+m-1,\, j+n-1}

  • 直观理解：将输出梯度（$\frac{\partial L}{\partial Y}$）与输入特征图做“相关运算”（cross-correlation）。

（2）对输入特征图的梯度（Input Gradient）

\frac{\partial L}{\partial X_{i,j}} = \sum_{m=1}^{k} \sum_{n=1}^{k} W_{m,n} \cdot \frac{\partial L}{\partial Y_{i-m+1,\, j-n+1}}

  • 直观理解：将输出梯度与翻转180°的卷积核做“全卷积”（full convolution）。

（3）对偏置的梯度（Bias Gradient）

\frac{\partial L}{\partial b} = \sum_{i,j} \frac{\partial L}{\partial Y_{i,j}}

三、推导直观说明与工程意义

  • 卷积核梯度：本质是用输出梯度“滑动”输入特征图，统计每个卷积核参数对损失的影响。

  • 输入梯度：本质是用输出梯度“滑动”翻转后的卷积核，传播误差信号至前一层。

  • 偏置梯度：对输出梯度求和即可。

这种结构保证了CNN参数共享、空间局部性等特性在反向传播中的高效实现。

四、实际案例：1D卷积反向传播推导与可视化

1. 简单1D卷积反向传播推导

假设输入 $x = [x_0, x_1, x_2, x_3]$，卷积核 $w = [w_0, w_1]$，输出 $y$ 为：

y_0 = w_0 x_0 + w_1 x_1 \\ y_1 = w_0 x_1 + w_1 x_2 \\ y_2 = w_0 x_2 + w_1 x_3

若损失对输出的梯度为 $\delta = [\delta_0, \delta_1, \delta_2]$，则：

  • 对卷积核的梯度：

    \frac{\partial L}{\partial w_0} = \delta_0 x_0 + \delta_1 x_1 + \delta_2 x_2 \\ \frac{\partial L}{\partial w_1} = \delta_0 x_1 + \delta_1 x_2 + \delta_2 x_3

  • 对输入的梯度（核翻转）：

    \frac{\partial L}{\partial x_0} = w_0 \delta_0 \\ \frac{\partial L}{\partial x_1} = w_1 \delta_0 + w_0 \delta_1 \\ \frac{\partial L}{\partial x_2} = w_1 \delta_1 + w_0 \delta_2 \\ \frac{\partial L}{\partial x_3} = w_1 \delta_2

2. 2D卷积反向传播可视化代码（PyTorch + Matplotlib）

下例以MNIST图片和自定义卷积核，演示前向卷积、反向传播（自动微分）和梯度可视化：

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from torchvision import datasets, transforms

# 数据加载
transform = transforms.Compose([transforms.ToTensor()])
testset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
image, label = testset[0]  # image: [1, 28, 28]

# 使输入支持梯度
img = image.unsqueeze(0).clone().detach().requires_grad_(True)  # [1, 1, 28, 28]

# 定义单层卷积
conv = nn.Conv2d(1, 1, kernel_size=3, stride=1, padding=1, bias=False)
with torch.no_grad():
    conv.weight[:] = torch.tensor([[[[1., 0., -1.], [1., 0., -1.], [1., 0., -1.]]]]) / 3  # 简单边缘核

# 前向传播
output = conv(img)
loss = output.sum()  # 假设损失为所有输出之和

# 反向传播
loss.backward()

# 可视化输入、卷积核、权重梯度、输入梯度
plt.figure(figsize=(12, 3))
plt.subplot(1, 4, 1)
plt.imshow(img[0, 0].detach().numpy(), cmap='gray')
plt.title('Input')
plt.axis('off')

plt.subplot(1, 4, 2)
plt.imshow(conv.weight.grad[0, 0].detach().numpy(), cmap='bwr')
plt.title('Weight Gradient')
plt.axis('off')

plt.subplot(1, 4, 3)
plt.imshow(conv.weight[0, 0].detach().numpy(), cmap='bwr')
plt.title('Kernel')
plt.axis('off')

plt.subplot(1, 4, 4)
plt.imshow(img.grad[0, 0].detach().numpy(), cmap='bwr')
plt.title('Input Gradient')
plt.axis('off')

plt.tight_layout()
plt.show()

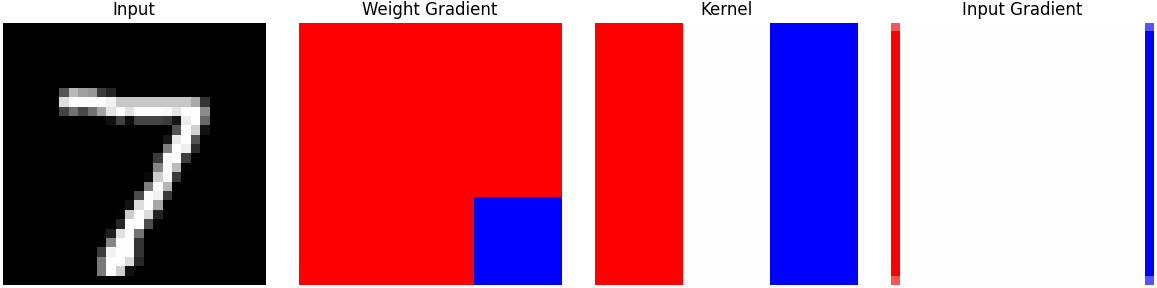
代码说明

  • 代码自动计算并可视化了输入、卷积核、权重梯度、输入梯度。

  • 可清楚看到梯度是如何“回流”到输入和权重的。

  • 你可以修改卷积核、损失函数等，观察梯度分布的变化。

运行效果

  • 脚本运行后会弹出一个窗口，依次显示原始输入、卷积核、卷积核的梯度、输入的梯度。

  • 你可以自由替换卷积核、损失函数等，观察梯度分布的变化，有助于深入理解CNN的反向传播机制。

五、工程实践建议

  • 理解梯度传播方向：权重梯度本质是“输入与输出梯度的相关”，输入梯度是“输出梯度与核的翻转相关”。

  • 多通道/多Batch场景：实际CNN中需在通道、Batch维度累加梯度，推导方式类似。

  • 自动微分框架：PyTorch、TensorFlow等已自动实现所有梯度推导，但理解底层原理有助于模型调试与创新。

  • 可视化调试：建议用上述代码实时可视化梯度，辅助理解和排查模型训练问题。

六、未来趋势与研究方向

随着深度学习理论和工程实践的不断演进，CNN中卷积层反向传播与梯度推导的研究和应用也在持续拓展，主要呈现以下趋势：

1. 自动微分与高效计算优化

  • 现代深度学习框架（如PyTorch、TensorFlow、JAX）已将卷积梯度推导与计算高度自动化和底层优化，支持GPU/TPU并行、混合精度训练和分布式大规模模型训练。

  • 未来，针对新型硬件（如AI芯片、神经形态计算）的专用卷积反向传播算法和高效实现将持续涌现。

2. 可解释性与可视化工具

  • 随着AI可解释性需求提升，卷积梯度的可视化（如Grad-CAM、特征归因等）成为模型调试、透明化和安全性分析的重要手段。

  • 未来研究将聚焦于更细粒度的梯度流追踪、跨层因果分析和模型决策路径解释，帮助工程师和用户理解CNN的“思考过程”。

3. 新型卷积算子与自适应梯度

  • 深度学习社区不断提出新型卷积算子（如可分离卷积、动态卷积、注意力卷积等），其反向传播机制和梯度推导也更加复杂和多样。

  • 研究者正探索自适应梯度、正则化梯度、噪声注入等新技术，提升模型泛化能力和鲁棒性。

4. 自动微分与符号推导的结合

  • 未来卷积梯度推导将更紧密结合符号计算、自动微分和机器学习理论，推动自动化模型验证、结构搜索（NAS）和理论可解释性研究。

5. 多模态与跨域卷积梯度

  • 随着多模态学习（如图像-文本、音频-视频等）和跨域迁移的兴起，卷积梯度推导方法将扩展到异构数据和复合结构，支持更复杂的AI系统和应用场景。

6. 教育与工程普及

  • 卷积反向传播的直观可视化、交互式教学工具和工程调试平台将不断丰富，降低深度学习入门和模型开发门槛，助力AI技术的普及和创新。

七、总结

卷积神经网络（CNN）中的反向传播与卷积梯度推导，是深度学习模型能够高效自我学习和不断优化的根本机制。通过对输入、卷积核和偏置的梯度精确计算，CNN能够在大规模数据和复杂空间结构中自动提取特征、调整参数，实现从低级边缘到高级语义的多层次感知与认知。

卷积梯度推导的工程价值体现在：

  • 支撑了端到端的模型训练，使得CNN能够在图像、语音、视频等多模态任务中持续提升表现；

  • 通过参数共享和局部连接，极大提升了模型的参数效率和泛化能力，降低了过拟合风险；

  • 反向传播的高效实现，为大规模分布式训练、自动微分和模型压缩等工程优化提供了基础。

理解卷积反向传播的理论与实践意义在于：

  • 帮助开发者深入理解模型训练的底层原理，提升调试、优化和创新能力；

  • 支持模型可解释性和安全性分析，便于定位问题、解释决策和提升AI系统的透明度；

  • 推动新型卷积算子、自动结构搜索、多模态融合等前沿技术的发展和落地。

展望未来，随着AI模型规模的持续扩展和应用场景的不断丰富，卷积梯度推导与反向传播机制将继续演进：自动微分与符号推导更加智能化，梯度可视化与可解释性工具更加丰富，新型算子和自适应梯度方法不断涌现，助力AI系统在更高维度、更复杂任务中实现突破。

掌握卷积反向传播与梯度推导的原理、推导方法和工程实现，是每一位深度学习工程师和研究者的必修课。只有深入理解这些基础机制，才能在AI系统设计、模型创新和实际应用中游刃有余，让CNN持续成为智能感知和认知世界的有力工具。

谢谢你看到这里，你们的每个赞、收藏跟转发都是我继续分享的动力。

如需进一步案例、代码实现或与其他聚类算法对比，欢迎留言交流！我是爱酱，我们下次再见，谢谢收看！

# 人工智能 # cnn # python # 机器学习 # 深度学习 # 神经网络
Logo
天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐

cover

【感知机】感知机(perceptron)学习算法例题及详解

avatar 天启AI社区
cover

AI云原生：数智化时代AI Agent加速落地的技术基石与实践指南（THS）

avatar 天启AI社区
cover

【AI论文】设计实验室：通过迭代检测与修正来设计幻灯片

avatar 天启AI社区