参考资料：python统计分析【托马斯】

        对于两个相关的变量，相关性度量的是两个变量之间的关联程度。相反，线性回归是用一个变量的值来预测另一个变量的值。

1、相关系数

        两个变量之间的相关系数回答了这个问题：“这两个变量有关系吗？”也就是说，如果一个变量的变化，那另一个也改变了吗？如果这两个变量是正态分布的，确定相关系数的标准方法通常是pearson，它是：

        其中，样本协方差被定义为：

        并且s_x和s_y分别是x和y的值的样本标准差，因此相关系数也可以写为：

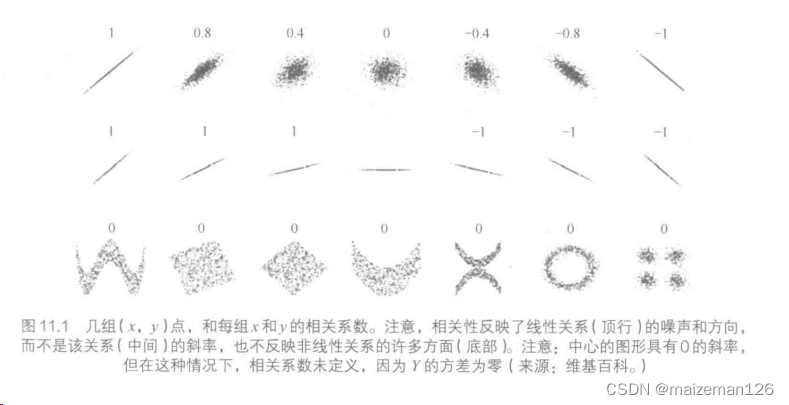
        pearson相关系数，有时也称为总体相关系数或样本相关性，它的取值范围是[-1,1]。注意相关系数的公式在x和y之间是对称的，但线性回归中不是这样的。

# 导入库
import numpy as np

x=np.array([18.5,18.7,19.1,19.7,21.5,21.7,21.8,22,23.4,23.8])
y=np.array([34,39,41,38,45,41,52,44,44,49])
np.corrcoef(x,y)

         当然要知道相关系数的显著性情况，可以使用stats.pearsonr()函数，如下：

from scipy import stats
r,p=stats.pearsonr(x,y)
print("相关系数：",r)
print("p值：",p)

        结论：x和y之间存在显著的相关性。

2、秩相关

        如果数据不是正态分布的，那么需要采用不同的方法。在这种情况下，我们可以对数据集的每个变量进行排序，比较这个顺序。计算秩相关的常用方法有两种。

        spearman's 和pearson相关系数r完全一样，但计算的不是原始的数字，二是观测值的秩。

        kendall's 也是一个秩相关系数，测量两个观测量之间的而相关。它比spearman's 更难计算，但是有争论认为spearman's 的置信区间比kendall's 参数的置信区间更不可靠和难以理解。

        spearman相关系数python计算如下：

import numpy as np
from scipy import stats
# 录入数据
x=np.array([12,7,4,9,7,2,9,5,8,4])
y=np.array([19,13,8,8,13,14,12,10,12,11])

rho,p=stats.spearmanr(x,y)
print("相关系数",rho)
print("p值",p)

        结论：x与y之相关性不显著。

        kendall相关系数python计算如下：

tau,p=stats.kendalltau(x,y)
print("相关系数：",tau)
print("p值：",p)