优化问题转变为强化学习问题（马尔科夫链决策）在能源系统领域目前还处于学术探讨阶段，有相关的文献，也有一些课题组正在研究，但我在工业界的了解（电力系统相关），没有出现过已经落实的方案。

根据本人之前的帖子对以下优化求解问题进行强化学习建模：

• 光储荷经济性调度，针对单个用户、单个光伏、单个储能设备，短周期内的经济最优目标

变量

• 充电变量：$X=(x_t)\in [0,\alpha ]$

• 放电变量：$Y=(y_t)\in [-\alpha ,0]$

• 储能设备能量状态：$S=(s_t)\in [0,1]$

以上三个变量为 continuous_var_list 连续变量列表

参数

• 负荷：load

• 功率：power

• 电价：price

• 充电效率：charge_efficiency

• 放电效率：discharge_efficiency

• 储能单次充放电限制：nominal_power

目标函数

最小化经济性最优目标：

$\text{minimize }Cost={\sum }_{t=1}^T(load(t)-power(t)+x(t)+y(t))\times price(t)÷costbase$

其中 costbase 为不使用储能的情况下的花费：

$costbase={\sum }_{t=1}^T(load(t)-power(t))\times price(t)$

约束条件

• 储能能量状态：

  • 储能初始状态为 0：$s_0=0$

  • 储能状态更新：$s_t=s_{t-1}+c_1\cdot x_t+\frac{y_t}{c_2}$

优化问题求解最优值：

• Total cost: -2.5496332782861244 （glpk）
• Total cost: -2.549633278286124 （scip）
• Total cost: -2.5496332782861235 （gurobi）
  不同求解器求解基本一致，详细代码参考我的另一篇帖子：基于Pyomo实现简单源网荷储场景的储能电站调度优化。

---

To 马尔科夫链如下：

1. 状态空间（State Space）

状态由以下四个变量组成，表示在当前时间步 ( t ) 下的系统状态：

• 用户负荷（user_load）: 当前时间步用户的电力需求。
• 电价（elec_price）: 当前时间步的电价。
• 光伏发电（pv_power）: 当前时间步分布式光伏发电量。
• 储能SOC（soc）: 当前时间步储能的状态（State of Charge）。

2. 动作空间（Action Space）

动作空间表示储能系统的充电或放电功率（以连续值定义）：

• 充电功率: $(a_t>0)$，表示充电。
• 放电功率: $(a_t<0)$，表示放电。
• 动作取值范围：$[-P_{\text{nominal}},P_{\text{nominal}}]$，其中 $P_{\text{nominal}}$ 是储能系统的最大充放电功率。

3. 状态转移（State Transition）

在当前时间步 $t$，根据动作$a_t$和当前状态$s_t$，下一个时间步的状态$s_{t+1}$.

4. 奖励函数（Reward Function）

奖励函数由以下部分组成，目标是最大化收益，最小化未满足需求和系统惩罚：

• 能源花费奖励：负荷未被满足的成本（取负值表示减少花费带来的奖励）。
  $R_{\text{energy}}=-\max (0,{\text{user\_load}}_t-({\text{pv\_power}}_t+a_t))$

• SOC惩罚：如果SOC超出合理范围（如SOC过高或过低），引入惩罚项。

6. 时间步与终止条件（Time Step and Termination Condition）

• 时间步: 每 10 分钟为一个时间步，全天共 144 步。
• 终止条件: 模拟到一天结束（144步）或达到最大时间步。

7. 策略优化目标

目标是通过策略 ( \pi(a_t | s_t) ) 最大化未来累积奖励：
${\pi }^{\ast }=\arg {\max }_{\pi }\mathbb{E}\left[{\sum }_{t=0}^T{\gamma }^t{R}_t\right]$

• $\gamma$: 折扣因子，用于平衡短期和长期奖励

代码如下：

1. 生成和优化求解项目中相同的测试数据

import random
import pandas as pd

# 设置随机种子
random.seed(1234)

# 创建时间序列数据
sampling_interval = 10  # 每10分钟采样一次
minutes_per_day = 24 * 60  # 一天共有1440分钟
time = minutes_per_day // sampling_interval  # 采样点数量

# 生成随机的用户负荷、用户功率和电价
user_loads = [round(random.uniform(0, 1), 2) for _ in range(time)]
user_powers = [round(random.uniform(0, 1), 2) for _ in range(time)]
elec_price = [round(0.5 + random.uniform(-0.2, 0.2), 2) for _ in range(time)]

# 生成光伏发电数据（模拟分布式能源）
pv_power = [round(random.uniform(0, 1), 2) for _ in range(time)]

# 创建时间序列
time_index = [f"{i // 6:02d}:{(i % 6) * 10:02d}" for i in range(time)]

# 整理为 DataFrame
data = pd.DataFrame({
    "time": time_index,
    "user_load": user_loads,
    "user_power": user_powers,
    "elec_price": elec_price,
    "pv_power": pv_power
})

# 查看数据
print(data.head())

# 保存数据到文件（可选）
data.to_csv("time_series_data.csv", index=False)

2. 生成用于强化学习agent训练学习的数据

time_per_day = minutes_per_day // sampling_interval  # 一天的采样点数量
days = 30  # 训练集的天数
# 生成训练集数据
training_data = []
for day in range(days):
    user_loads = [round(random.uniform(0, 1), 2) for _ in range(time_per_day)]
    user_powers = [round(random.uniform(0, 1), 2) for _ in range(time_per_day)]
    elec_price = [round(0.5 + random.uniform(-0.2, 0.2), 2) for _ in range(time_per_day)]
    pv_power = [round(random.uniform(0, 1), 2) for _ in range(time_per_day)]
    time_index = [f"Day {day + 1} {i // 6:02d}:{(i % 6) * 10:02d}" for i in range(time_per_day)]
    
    day_data = pd.DataFrame({
        "time": time_index,
        "user_load": user_loads,
        "user_power": user_powers,
        "elec_price": elec_price,
        "pv_power": pv_power
    })
    training_data.append(day_data)

# 合并所有天的数据
training_data = pd.concat(training_data, ignore_index=True)

# 保存数据到文件（可选）
training_data.to_csv("training_data_30_days.csv", index=False)

# 显示前几行数据
training_data.head()

3. 模型创建和训练

import pandas as pd
from stable_baselines3 import SAC
from stable_baselines3.common.callbacks import EvalCallback
from stable_baselines3.common.vec_env import DummyVecEnv
import numpy as np
import gym
from gym import spaces
import torch
# 自定义强化学习环境
class EnergyStorageEnv(gym.Env):
    def __init__(self, data, charge_eff=0.91, discharge_eff=0.95, nominal_power=0.8, soc_min=0.0, soc_max=0.8):
        super(EnergyStorageEnv, self).__init__()
        self.data = data.reset_index(drop=True)
        self.timestep = 0
        self.max_timesteps = len(data)
        
        # 参数设置
        self.charge_eff = charge_eff
        self.discharge_eff = discharge_eff
        self.nominal_power = nominal_power
        self.soc_min = soc_min
        self.soc_max = soc_max
        self.soc_penalty_factor = 100
        
        # 状态空间：用户负荷、电价、光伏发电、储能SOC
        self.observation_space = spaces.Box(low=0, high=1, shape=(4,), dtype=np.float32)
        
        # 动作空间：充电或放电功率 [-nominal_power, nominal_power]
        self.action_space = spaces.Box(low=-nominal_power, high=nominal_power, shape=(1,), dtype=np.float32)
    
    def reset(self):
        self.timestep = 0
        self.soc = 0  # 初始SOC
        self.state = self._get_state()
        return self.state
    
    def _get_state(self):
        # 当前状态：用户负荷、电价、光伏发电、储能SOC
        return np.array([
            self.data.iloc[self.timestep]['user_load'],
            self.data.iloc[self.timestep]['elec_price'],
            self.data.iloc[self.timestep]['pv_power'],
            self.soc
        ])
    
    def step(self, action):
        # 解析当前状态
        user_load = self.data.iloc[self.timestep]['user_load']
        elec_price = self.data.iloc[self.timestep]['elec_price']
        pv_power = self.data.iloc[self.timestep]['pv_power']
        
        # 动作限制
        action = np.clip(action[0], -self.nominal_power, self.nominal_power)
        
        # 更新SOC
        if action > 0:  # 充电
            self.soc += action * self.charge_eff
        else:  # 放电
            self.soc += action / self.discharge_eff
        
        # SOC限制及惩罚
        soc_penalty = 0
        if self.soc > self.soc_max:
            soc_penalty = -self.soc_penalty_factor * (self.soc - self.soc_max)
            self.soc = self.soc_max
        elif self.soc < self.soc_min:
            soc_penalty = -self.soc_penalty_factor * (self.soc_min - self.soc)
            self.soc = self.soc_min
        
        # 计算花费
        renewable_supply = pv_power + action
        grid_demand = max(0, user_load - renewable_supply)
        energy_cost = -grid_demand * elec_price  # 花费越低奖励越高
        
        # 奖励函数
        reward = energy_cost + soc_penalty
        
        # 更新状态
        self.timestep += 1
        done = self.timestep >= self.max_timesteps

        if not done:
            self.state = self._get_state()
        else:
            self.state = None
        
        return self.state, reward, done, {}
    
    def render(self, mode='human'):
        pass

# 加载训练和测试数据
train_data = pd.read_csv("training_data_30_days.csv")
test_data = pd.read_csv("time_series_data.csv")

# 创建强化学习环境
train_env = DummyVecEnv([lambda: EnergyStorageEnv(train_data)])
test_env = DummyVecEnv([lambda: EnergyStorageEnv(test_data)])

policy_kwargs = dict(
    net_arch=dict(
        pi=[256, 128, 128],  # 策略网络（Actor）
        qf=[256, 128,128]   # 价值网络（Critic）
    ),
    activation_fn=torch.nn.ReLU
)

# 定义SAC模型
model = SAC("MlpPolicy", train_env,policy_kwargs=policy_kwargs, verbose=1)

eval_callback = EvalCallback(test_env, eval_freq=5000, n_eval_episodes=5, verbose=1)
model.learn(total_timesteps=100000, callback=eval_callback)


# 测试模型性能
obs = test_env.reset()
total_rewards = 0
steps = 0

while True:
    action, _ = model.predict(obs, deterministic=True)
    obs, reward, done, _ = test_env.step(action)
    total_rewards += reward[0]
    steps += 1
    if done:
        break

print(f"Total Reward on Test Data: {total_rewards:.2f}")
print(f"Total Steps: {steps}")

4. 结果可视化

import matplotlib.pyplot as plt

# 重置环境以便测试
obs = test_env.reset()
step_rewards = []  # 存储每一步的奖励
actions = []  # 存储每一步的动作
soc_values = []  # 存储每一步的 SOC 值
unmet_demands = []  # 存储每一步的未满足负荷
timestamps = []  # 存储时间戳
total_rewards = 0
steps = 0

while True:
    action, _ = model.predict(obs, deterministic=True)  # 使用训练好的模型预测动作
    obs, reward, done, info = test_env.step(action)  # 环境执行动作并返回新的状态
    total_rewards += reward[0]
    steps += 1

    # 保存每步的信息
    step_rewards.append(reward[0])
    actions.append(action[0][0])  # 动作是二维，需要取第一个值
    soc_values.append(obs[0][-1])  # 状态的最后一项是 SOC
    unmet_demand = max(0, obs[0][0] - (obs[0][2] + action[0][0]))  # 未满足负荷 = 用户负荷 - (光伏 + 动作)
    unmet_demands.append(unmet_demand)
    timestamps.append(steps)

    if done:
        break

# 绘制结果
plt.figure(figsize=(14, 10))

# 1. 奖励值变化
plt.subplot(3, 1, 1)
plt.plot(timestamps, step_rewards, label="Step Rewards", color="b")
plt.xlabel("Time Step")
plt.ylabel("Reward")
plt.title("Step Rewards Over Time")
plt.legend()

# 2. 充放电决策
plt.subplot(3, 1, 2)
plt.plot(timestamps, actions, label="Charging/Discharging Power", color="g")
plt.axhline(0, color="r", linestyle="--", linewidth=0.7, label="Neutral Power")
plt.xlabel("Time Step")
plt.ylabel("Action (kW)")
plt.title("Charging (+) and Discharging (-) Decisions Over Time")
plt.legend()

# 3. SOC 变化和未满足负荷
plt.subplot(3, 1, 3)
plt.plot(timestamps, soc_values, label="SOC (State of Charge)", color="purple")
plt.plot(timestamps, unmet_demands, label="Unmet Demand", color="orange")
plt.xlabel("Time Step")
plt.ylabel("Value")
plt.title("SOC and Unmet Demand Over Time")
plt.legend()

plt.tight_layout()
plt.show()

print(f"Total Reward on Test Data: {total_rewards:.2f}")
print(f"Total Steps: {steps}")

5. 结果如图：

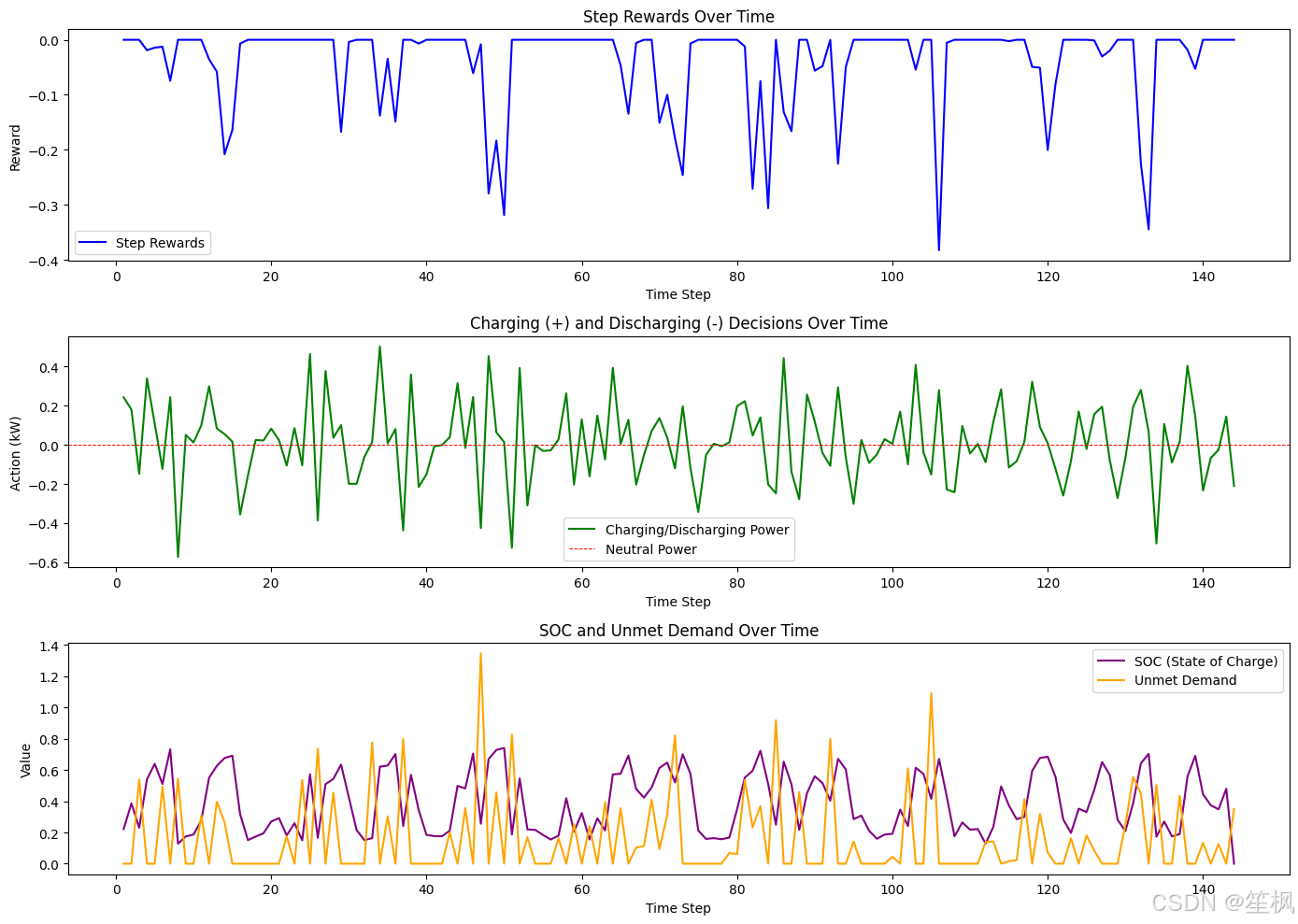
这里最终的求解结果Total Reward on Test Data: -5.67。和利用优化求解器求解是有区别的，包括约束并非每次都能很好的转化成奖励&惩罚。显而易见，求解器是从数学约束的角度找到了最优解（收敛点），而强化学习本身只是趋于最优解的一个代理。