4.1自回归

        自回归是一种时间序列预测方法，仅依赖于时间序列的先前输出：该技术假设下一个时间戳的未来观测值与先前时间戳的观测值存在线性关系。

       在自回归中，前一个时间戳的输出值成为预测下一个时间戳的输入值，并且误差遵循简单线性回归模型中关于误差的一般假设。在自回归中，时间序列中用于预测下一个时间戳的先前输入值的数量称为顺序（我们一般用字母p表示顺序）。该顺序值决定了将使用多少个先前的数据点：通常，数据科学家通过测试不同的值并观测使用最小的赤池信息量准则（AIC）得出的模型来估计p值。我们将在后面讨论（AIC）和贝叶斯信息量准则（BIC）惩罚似然准则。

        一阶自回归：将当前预测值（输出）基于紧接在前的值（输入）的自回归。

        二阶自回归：使用前两个值来预测下一个时间戳值。

        n阶自回归是多重线性回归，其中在任何时间t的序列值都是该同一时间序列中先前值的线性函数。由于这种序列依赖性，自回归的另一个重要方面是自相关：自相关是一种统计特性，当时间序列与其自身的之前或滞后版本线性相关时，就会出现这种特性。

        自相关是自回归的相关概念，输出（即需要预测的目标变量）和特定的滞后变量（即先前时间戳用作输入的一组值）之间的相关性越强，自回归赋予该特定变量的权重越大。因此该变量被认为具有很强的预测能力。

        参数方法：线性回归、普通最小二乘回归依赖于隐含的假设，即用于训练模型的训练集中不存在自相关。与他们一起使用的数据集呈现正态分布，并且它们的回归函数是根据有限数量的未知参数定义的，这些未知参数是从数据中估计得到的。

        因此，自相关可以帮助data scientist 为时间序列预测解决方案选择最合适的方法。此外自相关对于从数据和变量之间获得额外的洞察力以及识别隐藏的模式（如时间序列中的季节性和趋势）非常有用。

                

        data scientist 还经常使用自相关图 通过计算波动时滞后数据值的自相关性 来检查时间序列中的随机性。如果时间序列是随机的，则所有时间滞后的自相关值应该接近于零。如果时间序列不是随机的，那么一个或多个自相关将显著非零。

               

        由于ts data load 集非常精细，并且包含大量每小时的数据点，所以我们无法看到
应该在自相关图中显示的水平线。因此，我们可以创建数据集的子集(例如，可以选择
2014年8月的第一周)，然后再次应用自相关图函数，如下所示:

                

        如图4.5所示，自相关图显示了垂直轴上的自相关函数值。它的范围是-1到1。图
中显示的水平线对应于 95%和 99%置信区间，虚线对应于99%置信区间。自相关图旨
在揭示时间序列的数据点是正相关、负相关还是相互独立的。

        时间序列的滞后自相关图也称为自相关函数（ACF）。

        运行这些示例会创建两个二维图，分别显示x轴上的滞后值和y轴上-1和1之间的相关性。

                

                

        从这两个图中可以看出，置信区间被绘制成圆锥形。默认情况下，置信区间设置为95%，这表明该圆锥体之外的值很可能是相关的。

        如何理解95%的置信区间（超易懂）_哔哩哔哩_bilibili

       一个视频讲清楚置信区间！怎么理解、定义、评价、计算、与参考值区别，与P值关系_哔哩哔哩_bilibili

        一个视频搞清楚最大似然估计，6min超简单～_哔哩哔哩_bilibili

        另一个需要考虑的重要概念是部分相关函数（PACF），它是一种条件相关。假设我们考虑一些其他变量集的值，这就是两个变量之间的相关性。在回归中，可以通过关联两个不同回归的残差来找到这部分相关性。

        在时间序列数据集中，一个时间戳上的一个值和一个先前时间戳上的另一个值的自相关包括这两个值之间的直接相关性和间接相关性。这些间接相关性是观测值的相关性的线性函数，其值介于其间的时间戳值。

        python 用statsmodels库中的plot_pacf() 支持PACF函数。以下代码使用statsmodels库中的plot_pacf() 计算并绘制了ts_data_load集前20个滞后变量的部分自相关函数：

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(ts_data_load,lags=20)
pyplot.show()

        同样，以下代码使用statsmodels库中的plot_pacf()计算并绘制了ts_data_load子集的前30个滞后变量的部分自相关函数：

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(ts_data_load_subset,lags=30)
pyplot.show()

        当data scientist 需要理解和确定自回归和移动平均时间序列方法的顺序时，ACF和PACF函数的概念以及响应的图变得尤为重要。（#TODO 后面补充相应的视频来辅助理解）

        可以用两种方法来确定自回归AR(p)模型的顺序：

        方法一：ACF和PACF函数：

        方法二：信息准则

        

     

        ACF是一个自相关函数，可提供一系列与其滞后值自相关的信息。ACF描述了该序列的现值与其过去值之间的关系。

        时间序列数据集可以包含趋势、季节性和循环模式。ACF在寻找相关性时会考虑所有这些因素。（#TODO 趋势，季节性和循环模式）

        另一方面，PACF是另一个重要的函数，PACF不是像ACF一样找到当前值与滞后的相关性，而是找到残差与下一个滞后的相关性（#TODO）。此函数可以衡量增加一个滞后带来的增量效益。因此，如果通过PACF函数，我们发现残差中存在可以由下一个滞后建模的隐藏信息，可以获得良好的相关性，并且在建模时会将下一个滞后作为特征保留。

        为什么两个函数在建立自回归模型时很重要。因为自回归是一种基于以下假设的模型，即可以使用用一个时间序列的先前值获得时间序列的当前值：当前值是其过去值的加权平均。

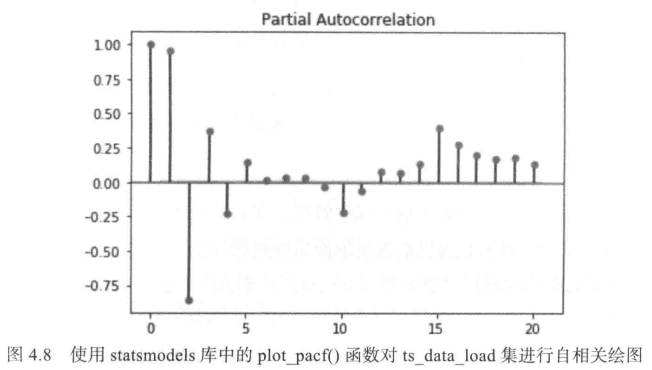
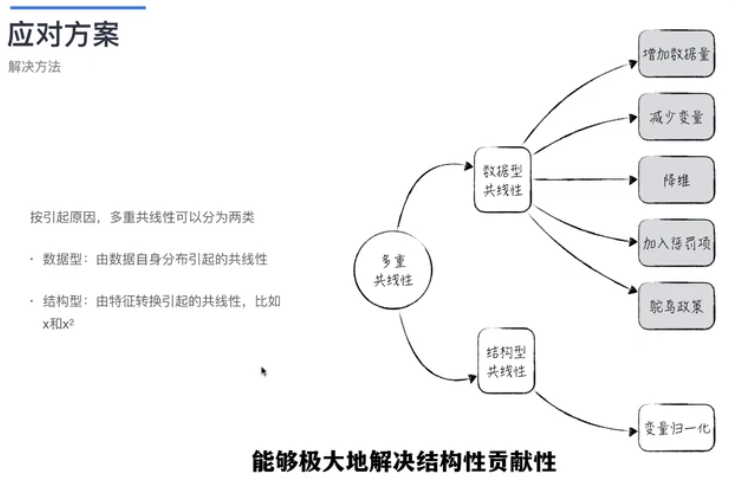
        为了避免时间序列模型的多重共线性特征，有必要使用PACF图找到自回归过程的最佳特征或顺序，因为它可以消除早期滞后解释的变化，因此仅获得相关特征(图4.8)。请注意，第六个滞后之前的滞后有很好的正相关性;这是ACF图切割置信上限的点。尽管在第六个滞后期之前都有良好的相关性，但不能全部使用它们，因为这会产生多重共线性问题;这就是为什么转向PACF图来仅获得最相关的滞后。

        多变量的烦恼：如何解决多重共线性问题_哔哩哔哩_bilibili     （推荐看一下）

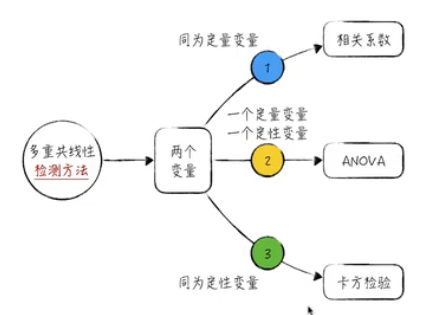
        多重共线性（Multicollinearity或Collinearity）源自对线性回归模型的深入研究。它是指在多变量线性模型中，特征之间存在高度相关关系，这会导致模型参数的估计不准确。

        

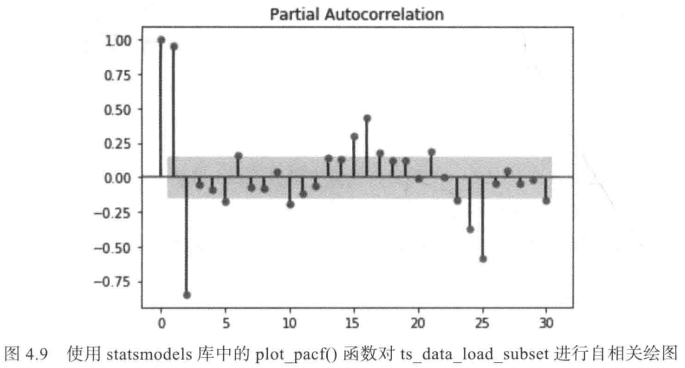
        在图4.9中可以看到，在图第一次切割上置信区间之前，最多6个后具有良好的相关性。这是p值，是自回归过程的顺序。我们可以使用前6个滞后的线性组合对给定的自回归过程进行建模。在图4.9中还可以看到在图第一次切割上置信区间之前，最多1个滞后具有良好的相关性。这是p值，是自回归过程的顺序。然后可以用第一个滞后为该自回归过程建模。

        模型中包含的滞后变量越多，模型对数据的拟合就越好。然而，这也代表有数据过度拟合的风险。信息量准则通过基于使用的参数数量施加惩罚来调整模型的拟合优度有两种流行的调整后的拟合优度指标：

        a.赤池信息量准则

        b.贝叶斯信息量准则

        为了从这两个度量中获取信息，可以使用Python中的summary()函数、params属性或赤池信息量准则和贝叶斯信息量准则属性。这些信息量准则用于拟合多个模型，每个模型具有不同数量的参数，并选择具有最低贝叶斯信息量准则的模型。（#TODO  示例说明）例如，如果有一个 AR(5)模型，则最低的信息量准则结果将表示值为5。

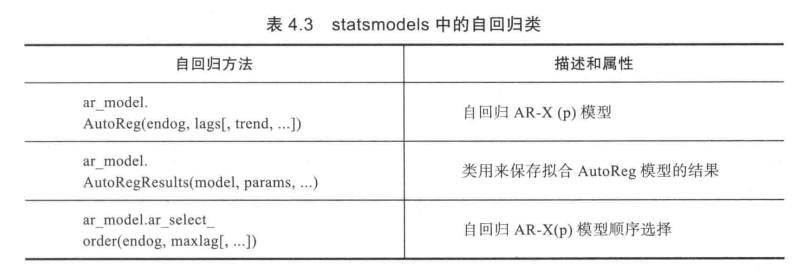
        从0.11 版本开始，statsmodels引入了一个专用于自回归的新类（statsmodels.org/stable/generated/statsmodels.tsa.ar_model.AutoReg.html）,如表4.3所总结。

        

        ar_model.AutoReg模型通过应用以下元素来估计参数：

                a.条件最大似然（CML）估计量：这是一种涉及条件对数似然函数的最大化的方法，据此认为已知的参数要么由理论假设固定，要么更常见的由估计值代替（LewisBeck、Bryman和Liao 2004）

        紧接着的内容请看下一个博客