一、学习目标

1.什么是线性规划？
2.线性规划的标准形式是什么？如何将一般形式转化为标准形式？
3.什么是单纯形法？

二、线性规划

1.线性规划（Linear programming，LP）的定义：将问题转化为数学模型后，模型中的所有公式都是线性公式时，这样的规划问题就是线性规划问题。
2.一个经典的线性规划案例，啤酒厂规划问题：有一家啤酒厂，
（1）每天卖出100箱啤酒，
（2）每天工作14小时，
（3）1小时可以生产10箱生啤酒，
（4）2小时可以生产10箱黑啤酒，
（5）1箱生啤酒卖20美元，
（6）1箱黑啤酒卖30美元，
问如何生产能得到最高收益。英文原描述如下：

显然，我们可以令x1为生啤酒的数量，x2为黑啤酒的数量，从而写出我们的数学模型：

运用高中知识，我们可以画出x1与x2的取值范围和z的等高线，如下图所示，可以发现，在（60，40）处可以达到最高效益。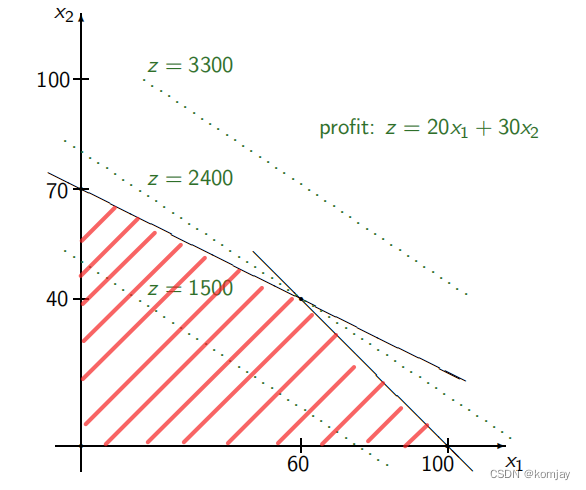

3.通过上面这个例子，想必大家明白什么线性规划问题以及人如何求解这个问题，但是想要计算机去解决这个问题，还需要把问题抽象化。

三、线性规划的标准形式

1.根据上面例子，我们可以得到以下的抽象化后的目标函数（红色）和约束条件（黄色）。

使用矩阵表示之后，还可以变为：

2.于是乎，我们得到了线性规划的基本形式：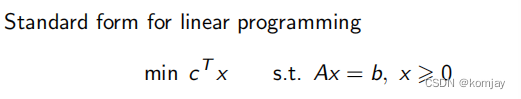

细心的同学可能发现了三个问题：
（1）啤酒厂案例中，我们是求max，而基本形式中一定要求求min；
（2）啤酒厂案例中，我们的约束条件是以不等式来约束的，在基本形式中，约束条件却是等式约束；
（3）一般情况中，x应该属于R，基本形式里却要求x一定要大于等于0。
而这三个问题也就对应了一般的线性规划问题如何变成线性规划的基本形式。

3.转化。

（1）求max与求min其实是一致的。只需要内外各取一次负值就行。
（2）首先如果是Ax≥b，两边需先取符号后，再给x新添一个维度s，使Ax+s=b即可。
（3）对于x属于R的情况，可以将x拆分为两个正值（x+与x-）相减，再代入目标函数和约束条件。

以啤酒厂案例为例，主要问题在于（2），原本约束条件为：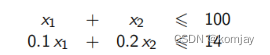

为了转化为等式，引入x3与x4：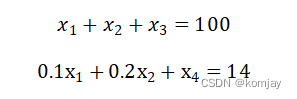

我们的A矩阵也就变成了：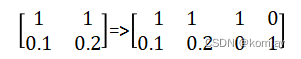

x向量也变为：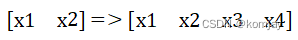

同理对于（3）步骤的改变也是同理。那么，我们花了这么大的功夫将一般形式转化为基本形式，到底为了什么呢？基本形式有什么作用呢？

四、单纯形法

1.将问题转化为基本形式的最主要目的就是让计算机能看明白问题描述，从而使用计算机算法去求解问题。接下来将讲述历史上第一个求解线性规划问题的方法：单纯形法（Simplex method）。
2.算法流程：分为两大步，共5小步。
（一-1）划分A矩阵和x向量：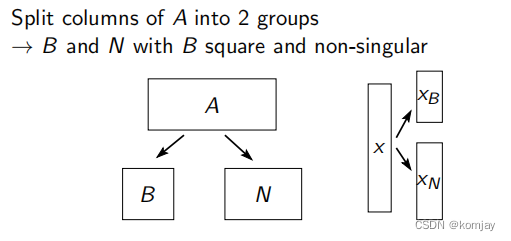

其中B矩阵是方阵，N是A剩余部分，x向量对应地划分为两部分，于是进行下一步：
（一-2）改写约束条件和目标函数：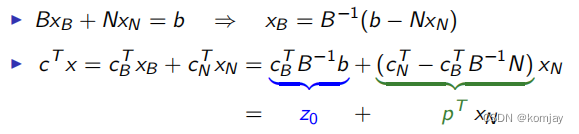

（一-3）得到一个基本解：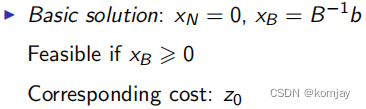

XN与XB是直接赋值的，其中原因我们就不讲解了，直接计算即可，当XB矩阵每个值都大于0，这个解就是一个可行解；如果不是，该解就是不在定义域内的，需舍弃。
（一-p.s.）以啤酒厂案例为例子，如果以下面的A来计算上面的公式

有：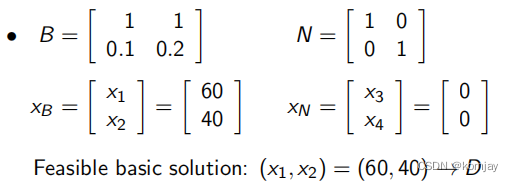
可以发现，这不就是我们的最优解了嘛？确实是的，但是在实际问题中，我们不一定能一开始就能找到最优解甚至是可行解。例如，根据矩阵行列可以互换的原则，我们交换A的第2列与第3列，A可以变为：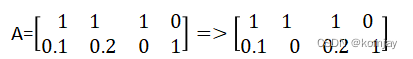

于是乎，我们继续计算（2）与（3），得到：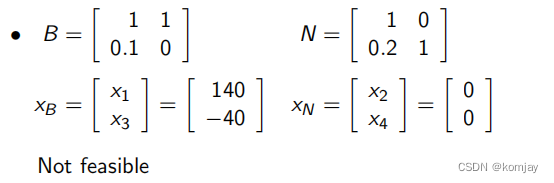

可以发现XB中的元素有负值，故是不可行解。

（二-1）于是我们可以发现，想要得到最优解，关键的步骤在于选择N中的第i列和B中的第j列，进行调换。如何选i和j是单纯形法的关键所在。首先i的选择

其中pi是（2）步骤中PT向量（黄色部分）中的第i个元素，选择其中值为负且最小的元素的下标i，这就是我们选择N的第i列。如果没有值为负，则说明达到最优解。提前结束优化。（唯一结束点）

在计算j之前，需要先算一个中间向量y，根据B*y=Ni计算出y向量，y的维度与XB的维度相同。

然后根据以下公式选择出j：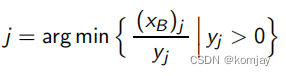

（二-2）持续运行（4）步骤。
（二-p.s.)为了更形象，我们还是以啤酒厂案例为例子，首先，我们以一个比较特殊的点（原点，红色展示）开始优化。选择i，j的依据为黄色部分。

交换B2heN2之后：

再交换B1和N1：

3.本节小节:对于啤酒厂案例，人工来求解几乎不需要使用这么麻烦的步骤，而对于计算机，其实也有两种办法：穷举法和单纯形法。有意识到的同学可能会发现，算法的第一大步已经可以让计算机计算出最优解，反正就是互换A矩阵的列，那我把A矩阵所有互换的情形都列出来，一共6种情况。在图中对应的就是：（红色标点）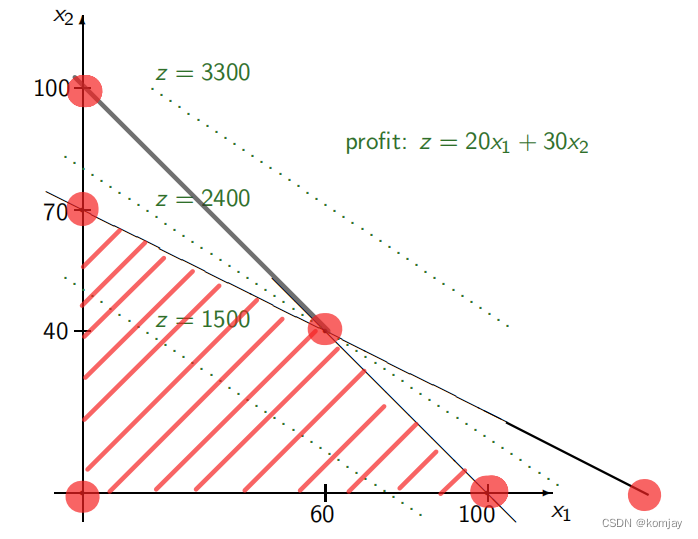

而对于单纯形法，我们其迭代路径如下所示（绿色箭头）：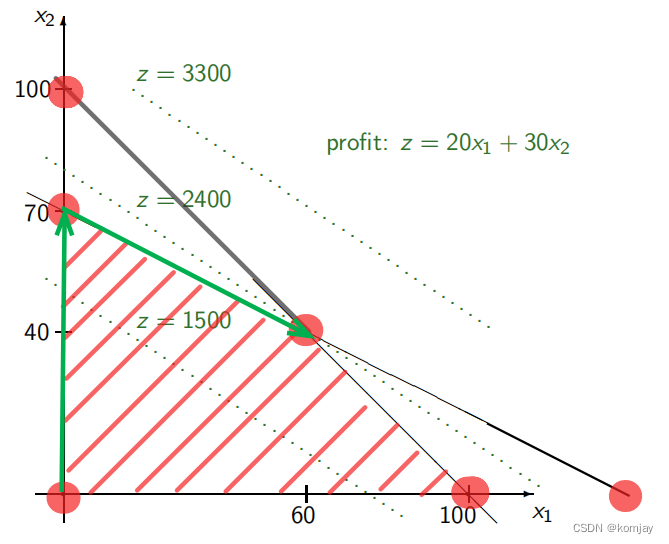

相比于穷举法，单纯形法可以显著减少计算次数，对于数量更多的未知数、更高维的约束条件，其性能提升能更加明显。

五、总结

1.了解了线性规划问题的内容
2.为了让问题能给以计算机计算，我们将模型进行抽象化、统一化，变为线性规划的基本形式
3.讲述了经典的线性规划的优化方法：单纯形法