机器学习笔记--2.逻辑回归模型

正值（如 1, 2）：通常表示成功收敛。注意查看x.shape,theta.shape,y.shape，确保数据格式准确，输出Cost(theta, x, y)：0.6931471805599453。可以发现构建了高次多项特征，而逻辑回归模型在训练时，若特征过多或模型复杂度较高（如引入高次多项式特征），容易出现过拟合现象，需要引入。，限制模型参数的大小，从而平衡模型的拟合能力与复杂度，提高模型的泛

2301_82125033

934人浏览 · 2025-07-08 23:18:57

2301_82125033 · 2025-07-08 23:18:57 发布

一、模型概述

逻辑回归模型（Logistics Regression）适用于二分类问题，核心思想：

1.线性模型

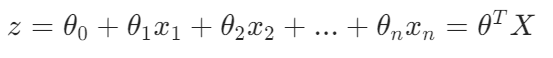
2.sigmoid 函数

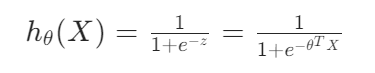
图像表达：

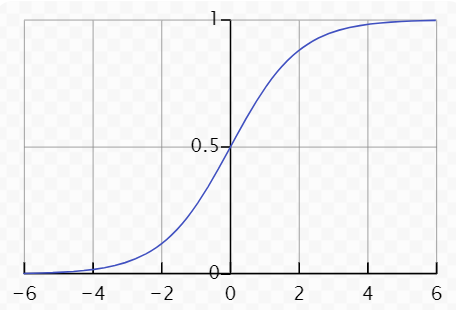
3.设置阈值

若 $h_{ \theta }(x)\geqslant 0.5$ ，预测为正类（y=1）

若 $h_{\theta }(x)< 0.5$ ，预测为负类（y=0）

4.决策边界

由 $h_{\theta }(x)=0.5$ 得，推导出 $z=\theta ^{T}X=0$ ，决策边界方程：

线性决策边界：直接使用原始特征（如 x1，x2）等
非线性决策边界：通过多项式特征（如 x1^2，x1*x2等)，扩展线性模型。

5.代价函数

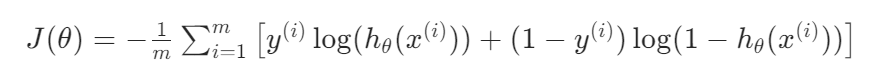
二、代码练习

1.线性决策边界

通过一段代码练习实现。

首先读取数据，可视化原始数据观察

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.optimize as opt
from sklearn.metrics import classification_report  #这个包是评价报告

sns.set(context='notebook',style='whitegrid') #设置视图格式

#读取数据
data1=pd.read_csv('ex2data1.txt',names=['text1','text2', 'admitted'])

#原始数据可视化
positive=data1[data1['admitted'].isin([1])]
negative=data1[data1['admitted'].isin([0])]  # isin为筛选函数，区分0,1不同的数据

fig, ax = plt.subplots(figsize=(12,8))  #figsize 设置图形的大小
ax.scatter(positive['text1'], positive['text2'], s=50, c='b', marker='o', label='admitted')   #散点大小s设置为50,颜色参数c为蓝色，散点形状参数marker为圈
ax.scatter(negative['text1'], negative['text2'], s=50, c='r', marker='x', label='not admitted')#散点大小s设置为50,颜色参数c为红色，散点形状参数marker为叉
ax.legend()   #显示图例
ax.set_xlabel('text 1 Score')  #设置x轴变量
ax.set_ylabel('text 2 Score')   #设置y轴变量
plt.show()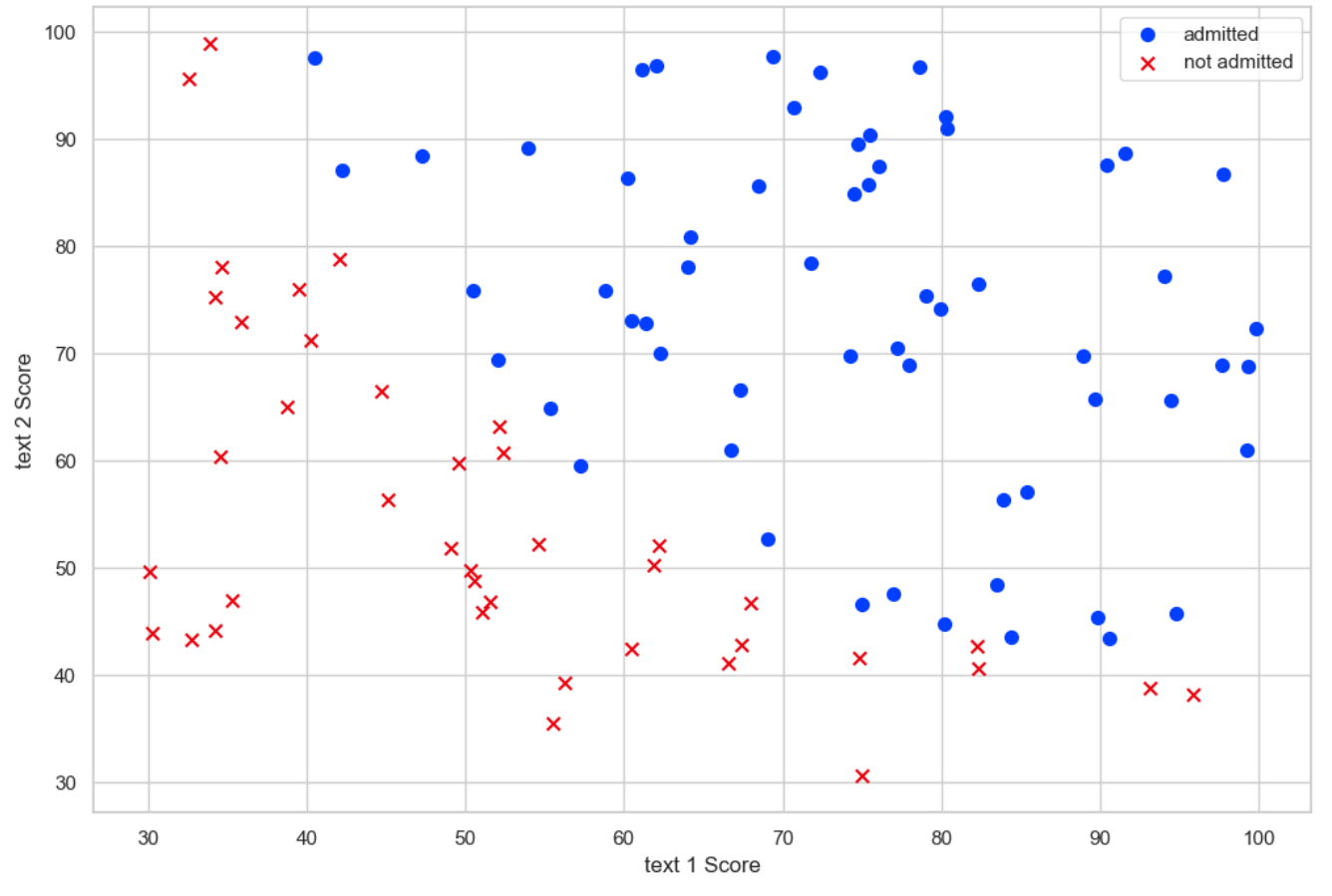

如图所示，原始数据集的分布，接近于线性决策边界。

接下来，定义sigmoid函数：

def sigmoid(z):
    g = 1/(1+np.exp(-z))
    return g

代价函数：

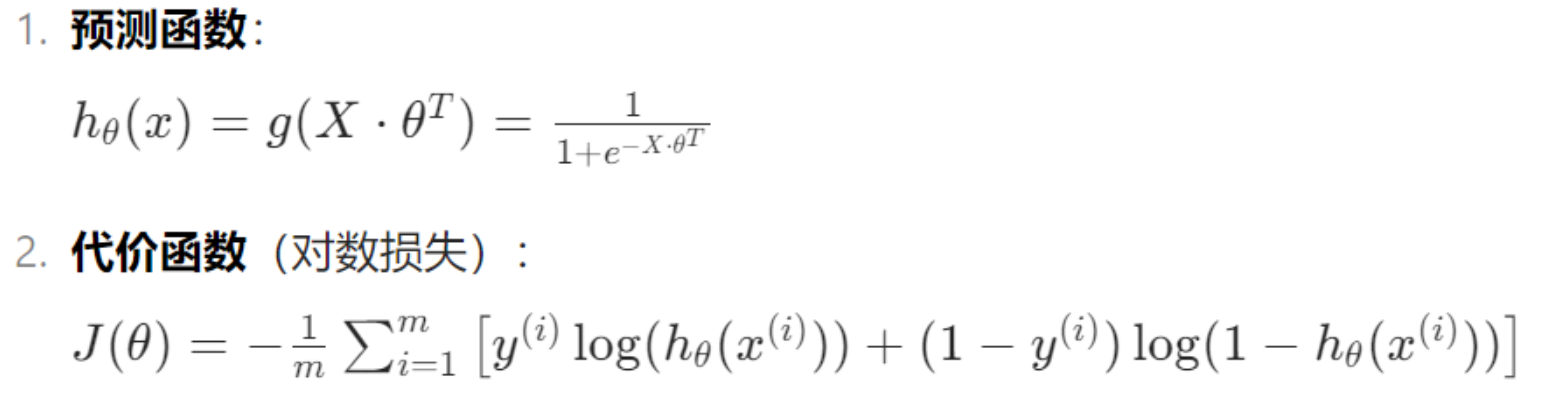
def Cost(theta, x, y):
    x=np.matrix(x)  #转化为矩阵形式
    y=np.matrix(y)
    theta=np.matrix(theta)

    #代价函数公式
    first=np.multiply(-y,np.log(sigmoid(x*theta.T)))
    second=np.multiply((1-y),np.log(1-sigmoid(x*theta.T)))
    J=np.sum(first-second)/(len(x))

    return J

data1.insert(0, 'Ones', 1)   #在第0列插入表头为“ONEs”的列，数值为1
cols = data1.shape[1]   #获取表格df的列数
x = data1.iloc[:,0:cols-1]   
y = data1.iloc[:,cols-1:cols]  

x = np.array(x.values)  #转换为数组
y = np.array(y.values) 
theta = np.zeros(3)   #初始化theta数组为(0,0,0)

注意查看x.shape,theta.shape,y.shape，确保数据格式准确，输出Cost(theta, x, y)：0.6931471805599453

定义梯度函数：

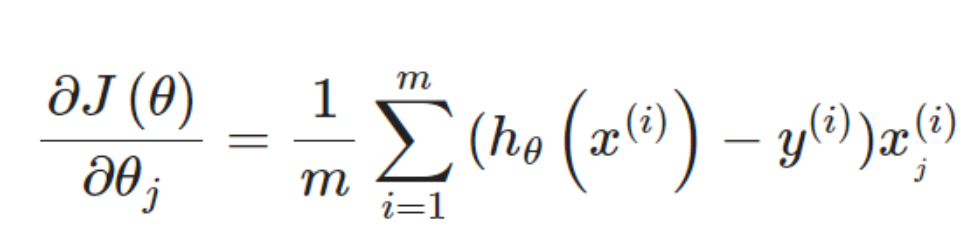
def gradient(theta, x, y):
    x=np.matrix(x)
    y=np.matrix(y)
    theta=np.matrix(theta)  #转换成矩阵形式

    parameters= int(theta.ravel().shape[1])    #获取参数数量
    grad=np.zeros(parameters)   #初始化梯度向量

    error=sigmoid(x*theta.T)-y  #计算误差

    for i in range(parameters):
        term=np.multiply(error,x[:,i])  #误差与第i个特征乘积
        grad[i]=np.sum(term)/len(x)    #计算平均梯度
        
    return grad

实际上没有在这个函数中执行梯度下降，仅仅在计算一个梯度步长。fmin_tnc 是一个优化函数，采用截断牛顿法（Truncated Newton Method）寻找函数的最小值。在逻辑回归中，它用于最小化对数损失函数，找到最优参数 θ。手动实现梯度下降需要编写迭代循环，而 fmin_tnc 自动完成迭代过程，返回最优参数。

import scipy.optimize as opt
result = opt.fmin_tnc(func=Cost, x0=theta, fprime=gradient, args=(x, y)) 
result

输出结果：(array([-25.16131863, 0.20623159, 0.20147149]), 36, 0)

result中输出的值：
result[0]为最优参数θ的截距项和特征权重
result[1]为优化算法的迭代次数
result[2]收敛状态码，表示优化结果的状态。0：优化成功，达到收敛条件。正值（如 1, 2）：通常表示成功收敛。负值（如 - 1, -2）：表示优化失败（如超出最大迭代次数、梯度计算错误等）

之后，寻找决策边界。决策边界分为

线性决策边界：

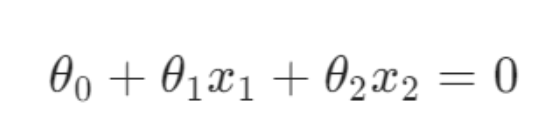
也可整理成：

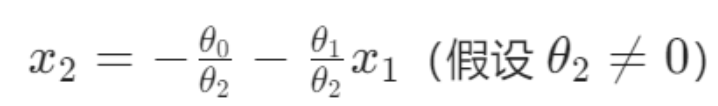
非线性决策边界：

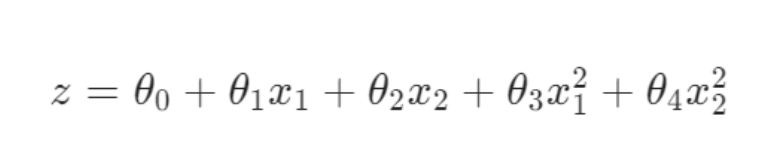
上述数据集分布更接近于线性决策边界，而得出的result[0]为最优参数θ的截距项和特征权重，编写如下代码：

coef=-(result[0]/((result[0])[2]))  #将result[0]中每一个数除以result[0]中的三个元素，然后取相反值

print(coef)得出

[124.88774019  -1.02362668  -1.        ]

x=np.arange(130,step=0.1)   #由于截距小于125，这里设置终点为130
y=coef[0]+coef[1]*x

接下来，可视化决策边界：

sns.lmplot(x='text1', y='text2', data=data1,  # 明确指定 x 和 y
           hue='admitted', 
           height=6,  # 在Seaborn v0.9.0之后，size参数改名为height
           fit_reg=False,   
           scatter_kws={"s": 25}  
          )
plt.plot(x, y, 'grey') #plot为画图函数，plot(x变量，y变量，‘线条颜色和；类型’)，设置线条颜色为灰色
plt.xlim(0, 130)  #设置x轴的范围
plt.ylim(0, 130) #设置y轴的范围
plt.title('Decision Boundary')  #设置标题
plt.show()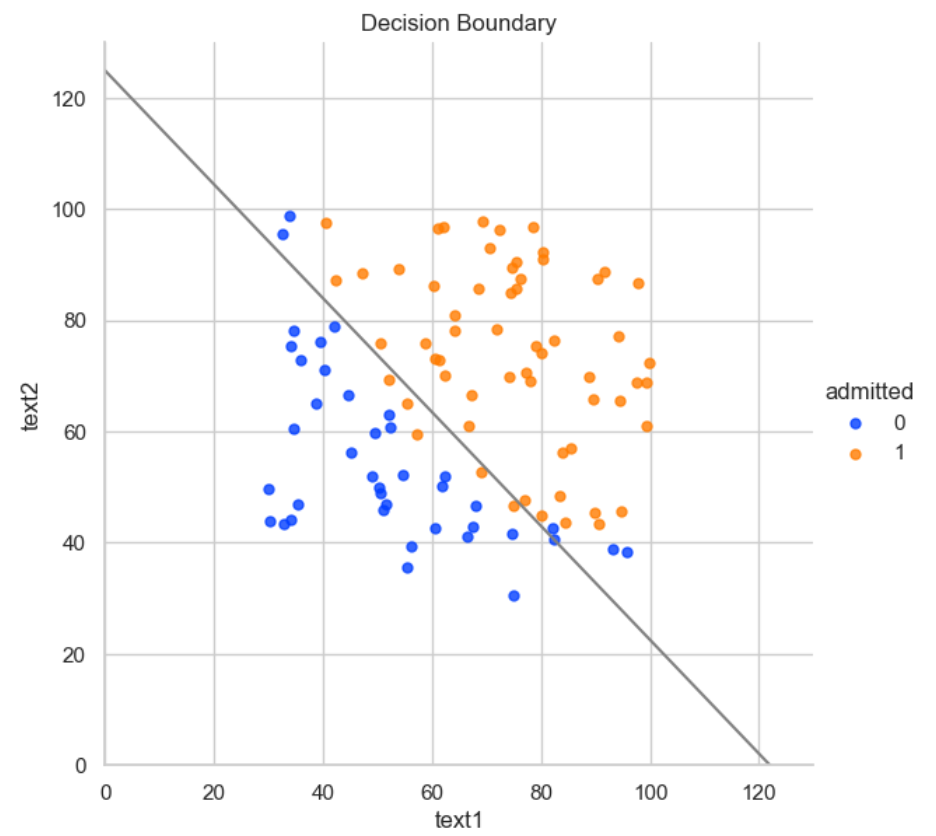

2.非线性决策边界

上述案例为线性决策边界，接下来针对非线性决策边界编码。

首先还是可视化数据，进行观察：

data2=pd.read_csv('ex2data2.txt',names=['text1','text2', 'accepted'])

positive=data2[data2['accepted'].isin([1])]
negative=data2[data2['accepted'].isin([0])]  # isin为筛选函数，区分0,1不同的数据

fig, ax = plt.subplots(figsize=(12,8))  #figsize 设置图形的大小
ax.scatter(positive['text1'], positive['text2'], s=50, c='b', marker='o', label='accepted')   #散点大小s设置为50,颜色参数c为蓝色，散点形状参数marker为圈
ax.scatter(negative['text1'], negative['text2'], s=50, c='r', marker='x', label='not accepted')#散点大小s设置为50,颜色参数c为红色，散点形状参数marker为叉
ax.legend()   #显示图例
ax.set_xlabel('text 1 Score')  #设置x轴变量
ax.set_ylabel('text 2 Score')   #设置y轴变量
plt.show()

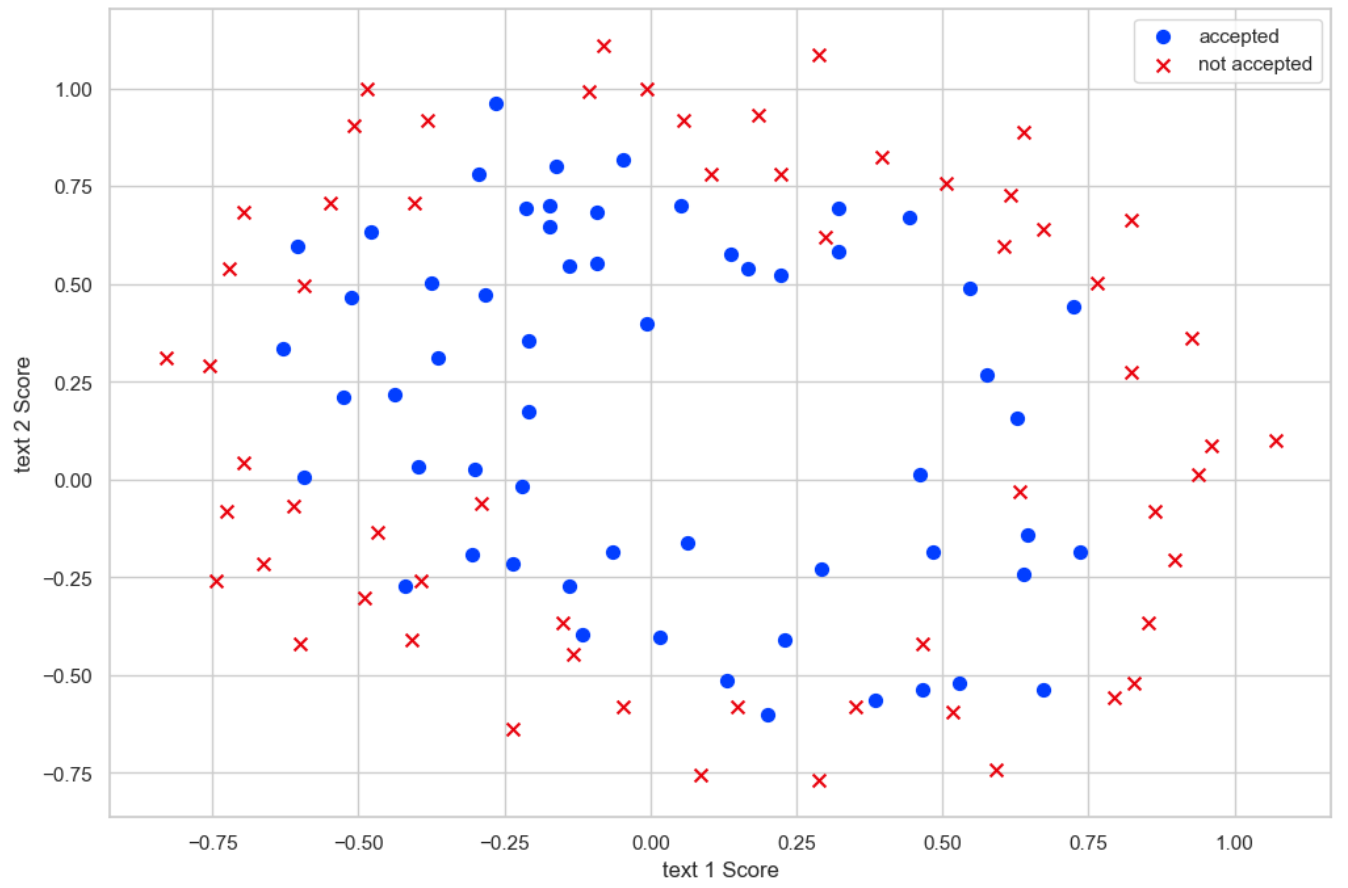如图所示，数据分布符合非线性决策边界。需要构建多项式特征，通过多项式特征，模型可以捕捉特征之间的非线性关系。例如：原始特征 text1 和 text2 可能无法线性区分数据。多项式特征 text1^2 或 text1*text2 可能揭示隐藏的模式。这在逻辑回归中特别有用，因为它将线性决策边界转换为非线性边界（如圆形、椭圆形等）。编码如下：

degree = 5  #生成最高 4 次幂的多项式特征
x1 = data2['text1']
x2 = data2['text2']

data2.insert(3, 'Ones', 1)   #在第4列插入标题为One,各行值为1的列，相当于线性模型中的截距项。

for i in range(1, degree):
    for j in range(0, i):
        data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)
        #np.power(A,B)   ## 对A中的每个元素求B次方


data2.drop('text1', axis=1, inplace=True) #删除表头为Test 1的列，axis=1表示默认删除行或列，inplace=True表示原数组被data2替换.
data2.drop('text2', axis=1, inplace=True) #删除原始特征

data2.head()

构建多项特征之后的数据如下：

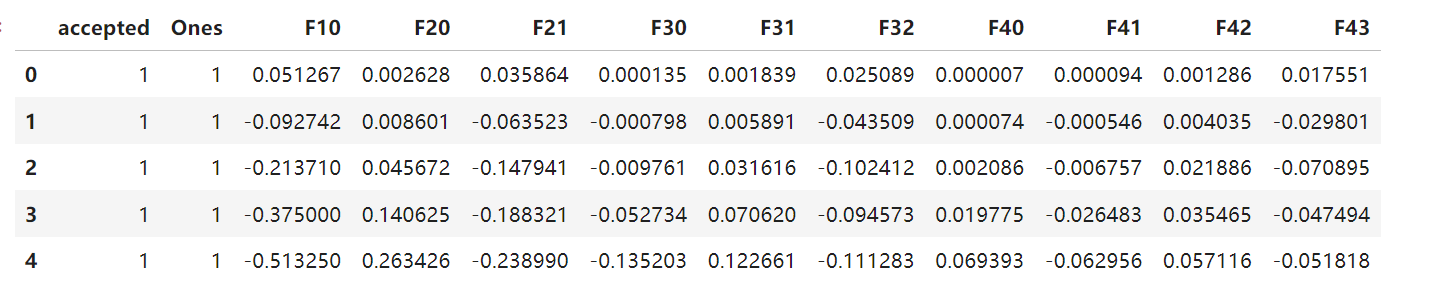
可以发现构建了高次多项特征，而逻辑回归模型在训练时，若特征过多或模型复杂度较高（如引入高次多项式特征），容易出现过拟合现象，需要引入正则化的方法来防止模型过拟合。

正则化通过在代价函数中添加一个惩罚项，限制模型参数的大小，从而平衡模型的拟合能力与复杂度，提高模型的泛化能力（对新数据的预测性能）。

那么正则化具体是什么东西呢？

正则化通过在逻辑回归的代价函数中添加一个惩罚项来实现。逻辑回归的原始代价函数（对数损失）为：

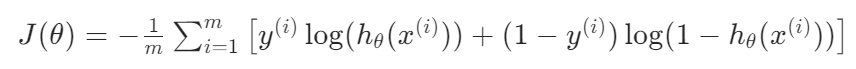
添加正则化项后，代价函数变为：

以上是我总结后的简化版本，详细解释可参考吴恩达老师的机器学习课程，更加全面，更加通俗易懂。

接下来，定义代价函数（添加惩罚项）：

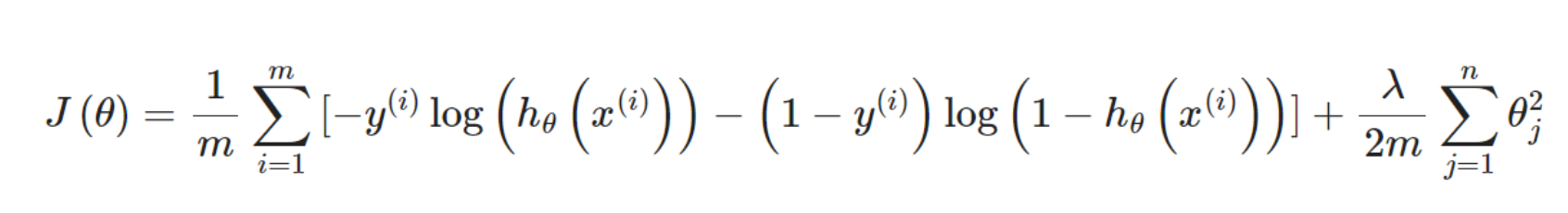
def Costreg(theta,x, y,learningRate):
    x=np.matrix(x)
    y=np.matrix(y)
    theta=np.matrix(theta)

    first=np.multiply(-y,np.log(sigmoid(x*theta.T)))
    second=np.multiply((1-y),np.log(1-sigmoid(x*theta.T)))
    reg=(learningRate/(2*len(x)))*np.sum(np.power(theta[:,1:theta.shape[1]],2))
    J=np.sum(first-second)/len(x)+reg

    return J

定义梯度下降函数（引入正则化）：

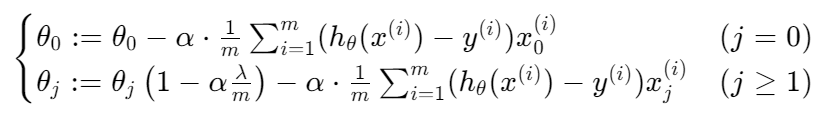
def gradientReg(theta,x, y,learningRate):
    x=np.matrix(x)
    y=np.matrix(y)
    theta=np.matrix(theta)  #转换成矩阵形式

    parameters=int(theta.ravel().shape[1])  #获取参数数量
    grad=np.zeros(parameters)   #初始化梯度向量

    error=sigmoid(x*theta.T)-y  #计算误差

    for i in range(parameters):
        term=np.multiply(error,x[:,i])  #误差与第i个特征乘积

        if(i==0):
            grad[i]=np.sum(term)/len(x)  # 普通梯度计算，无正则化
        else:
            grad[i]=np.sum(term)/len(x)+(learningRate/len(x))*theta[:,i]   # 梯度 = 普通梯度 + 正则化项 (λ/m)·θ_j
        
    return grad

定义好函数之后，对数据进行处理：

cols = data2.shape[1]  #获取data2的列数
x2 = data2.iloc[:,1:cols] #取所有列每一行的数据
y2 = data2.iloc[:,0:1] #取第一和第二列每一行的数据

x2 = np.array(x2.values) #将数值转换为数组
y2 = np.array(y2.values)
theta2 = np.zeros(11) #创建长度为11的零数组

learningRate=1

同样需要注意x2，y2，theta2的数据格式，然后利用上述的fmin_tnc优化函数来自动帮忙寻找最优参数θ：

result2 = opt.fmin_tnc(func=Costreg, x0=theta2, fprime=gradientReg, args=(x2, y2, learningRate))
result2

得到：(array([ 0.53010247, 0.29075567, -1.60725764, -0.58213819, 0.01781027,
-0.21329507, -0.40024142, -1.3714414 , 0.02264304, -0.95033581,
0.0344085 ]), 22,1)

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐