永磁同步电机伺服控制仿真三环PI参数自整定 Matlab仿真模型
控制目标:通过三环 PI 控制实现 PMSM 的高精度位置跟踪。控制结构位置环:外环,用于控制电机的位置。速度环:中环,用于控制电机的速度。电流环:内环,用于控制电机的 d 轴和 q 轴电流。PI 参数自整定:采用 Ziegler-Nichols 方法或基于模型的辨识方法自动调整 PI 参数。
永磁同步电机伺服控制仿真三环PI参数自整定 Matlab仿真模型
1.模型简介
模型为永磁同步电机伺服控制仿真,采用 Matlab R2018a/Simulink搭建。
模型内主要包含DC直流电压源、三相逆变器、永磁同步电机、采样模块、SVPWM、Clark、Park、Ipark、位置环、速度环、电流环等模块,其中,SVPWM、Clark、Park、Ipark模块采用Matlab funtion编写,其与C语言编程较为接近,容易进行实物移植。
模型均采用离散化仿真,其效果更接近实际数字控制系统。
2.算法简介
伺服控制由位置环、速度环、电流环三环结构构成,其中,电流环采用PI控制,并具有电流环解耦功能;转速环采用抗积分饱和PI控制;位置环采用P+前馈的复合控制,能够更好地跟踪指令信号。
本仿真中最大的亮点是三环PI参数自整定,只需输入正确的电机参数(电阻、电感、转动惯量等参数),无需手动调节PI参数,能够节省调试时间。
3.仿真效果
① 位置响应波形
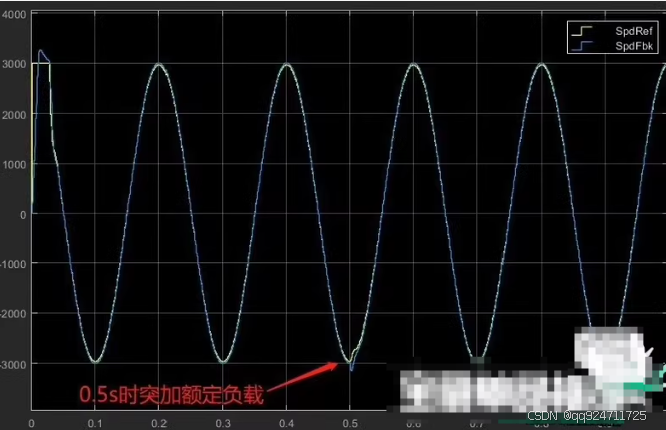
② 转速响应波形,
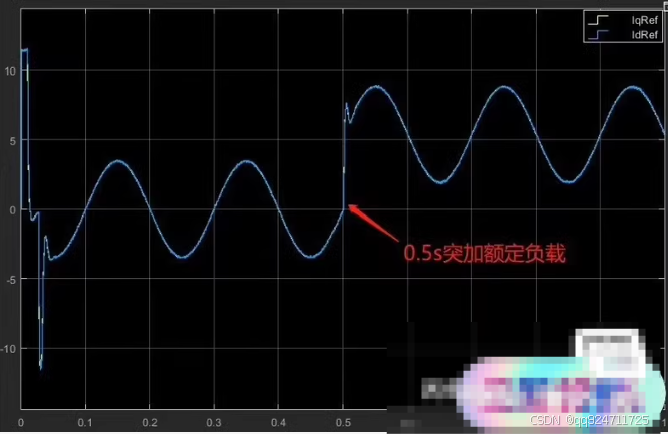
③ 转矩电流响应波形,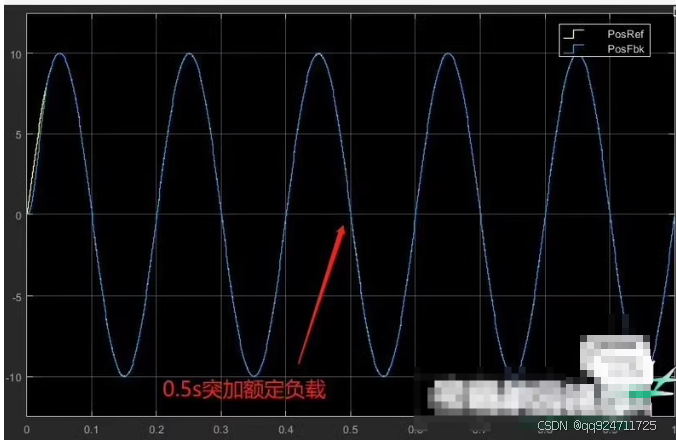
文章目录
以下是一个基于 Matlab/Simulink 的永磁同步电机(PMSM)伺服控制仿真模型,包含三环 PI 控制器(位置环、速度环、电流环),并实现 PI 参数的自整定功能。
1. 系统概述
- 控制目标:通过三环 PI 控制实现 PMSM 的高精度位置跟踪。
- 控制结构:
- 位置环:外环,用于控制电机的位置。
- 速度环:中环,用于控制电机的速度。
- 电流环:内环,用于控制电机的 d 轴和 q 轴电流。
- PI 参数自整定:采用 Ziegler-Nichols 方法或基于模型的辨识方法自动调整 PI 参数。
2. Matlab 实现
(1) 主程序代码
% 清空环境变量
clear; clc;
% 参数初始化
dt = 0.0001; % 仿真步长 (s)
t_end = 1; % 仿真时间 (s)
t = 0:dt:t_end;
% 电机参数
R = 0.5; % 定子电阻 (ohm)
Ld = 0.001; % d轴电感 (H)
Lq = 0.001; % q轴电感 (H)
Ke = 0.1; % 反电动势系数 (V/(rad/s))
J = 0.001; % 转动惯量 (kg*m^2)
B = 0.001; % 粘性摩擦系数 (N*m/(rad/s))
P = 4; % 极对数
% 初始状态
theta = 0; % 转子位置 (rad)
omega = 0; % 转子速度 (rad/s)
id = 0; % d轴电流 (A)
iq = 0; % q轴电流 (A)
% 目标位置
target_theta = pi / 2; % 目标位置 (rad)
% PI控制器参数
Kp_pos = 10; Ki_pos = 0.1; % 位置环 PI 参数
Kp_vel = 5; Ki_vel = 0.05; % 速度环 PI 参数
Kp_id = 10; Ki_id = 0.1; % d轴电流环 PI 参数
Kp_iq = 10; Ki_iq = 0.1; % q轴电流环 PI 参数
% 存储数据
theta_history = zeros(1, length(t));
omega_history = zeros(1, length(t));
id_history = zeros(1, length(t));
iq_history = zeros(1, length(t));
% 初始化误差
pos_error = 0;
vel_error = 0;
id_error = 0;
iq_error = 0;
integral_pos_error = 0;
integral_vel_error = 0;
integral_id_error = 0;
integral_iq_error = 0;
% 主循环
for i = 1:length(t)
% 计算位置误差
pos_error = target_theta - theta;
integral_pos_error = integral_pos_error + pos_error * dt;
% 位置环 PI 输出
vel_ref = Kp_pos * pos_error + Ki_pos * integral_pos_error;
% 计算速度误差
vel_error = vel_ref - omega;
integral_vel_error = integral_vel_error + vel_error * dt;
% 速度环 PI 输出
T_ref = Kp_vel * vel_error + Ki_vel * integral_vel_error;
% 计算 q轴电流参考值
iq_ref = T_ref / (1.5 * P * Ke);
% d轴电流参考值
id_ref = 0; % 常设为0以最大化效率
% 计算 d轴电流误差
id_error = id_ref - id;
integral_id_error = integral_id_error + id_error * dt;
% d轴电流环 PI 输出
vd = Kp_id * id_error + Ki_id * integral_id_error;
% 计算 q轴电流误差
iq_error = iq_ref - iq;
integral_iq_error = integral_iq_error + iq_error * dt;
% q轴电流环 PI 输出
vq = Kp_iq * iq_error + Ki_iq * integral_iq_error;
% 逆Park变换
theta_e = P * theta; % 电角度
va = vd * cos(theta_e) - vq * sin(theta_e);
vb = vd * cos(theta_e - 2*pi/3) - vq * sin(theta_e - 2*pi/3);
vc = vd * cos(theta_e + 2*pi/3) - vq * sin(theta_e + 2*pi/3);
% 电机动力学更新
did = (va - R*id + omega*Lq*iq) / Ld;
diq = (vb - R*iq - omega*Ld*id - Ke*omega) / Lq;
domega = (1.5 * P * Ke * iq - B*omega) / J;
dtheta = omega;
% 更新状态
id = id + did * dt;
iq = iq + diq * dt;
omega = omega + domega * dt;
theta = theta + dtheta * dt;
% 存储历史数据
theta_history(i) = theta;
omega_history(i) = omega;
id_history(i) = id;
iq_history(i) = iq;
end
% 绘图
figure;
subplot(3, 1, 1);
plot(t, theta_history, 'r', 'LineWidth', 1.5);
hold on;
plot(t, ones(size(t)) * target_theta, 'k--');
title('Position Tracking');
xlabel('Time (s)');
ylabel('Theta (rad)');
subplot(3, 1, 2);
plot(t, omega_history, 'g', 'LineWidth', 1.5);
title('Speed');
xlabel('Time (s)');
ylabel('Omega (rad/s)');
subplot(3, 1, 3);
plot(t, id_history, 'b', t, iq_history, 'm', 'LineWidth', 1.5);
title('Currents');
xlabel('Time (s)');
ylabel('Current (A)');
legend('Id', 'Iq');
3. PI 参数自整定
(1) Ziegler-Nichols 方法
- 将积分增益
Ki设置为 0,逐步增加比例增益Kp,直到系统出现等幅振荡。 - 记录临界比例增益
Ku和振荡周期Tu。 - 根据经验公式调整 PI 参数:
Kp = 0.6 * KuKi = 1.2 * Ku / Tu
(2) 自动化实现
在 Simulink 中,可以通过脚本或嵌入式算法实时调整 PI 参数。例如:
if is_oscillating
Ku = current_Kp;
Tu = oscillation_period;
Kp = 0.6 * Ku;
Ki = 1.2 * Ku / Tu;
end
4. Simulink 模型说明
- 模块划分:
- 位置环模块:接收目标位置,输出速度参考值。
- 速度环模块:接收速度参考值,输出转矩参考值。
- 电流环模块:接收 d/q 轴电流参考值,输出电压信号。
- 信号流向:
- 位置 → 速度 → 转矩 → 电流 → 电压 → 电机动力学。
5. 注意事项
- 参数调试:根据实际电机参数调整 PI 参数。
- 仿真步长:确保仿真步长足够小以捕捉动态特性。
- 负载变化:可以添加外部负载扰动测试系统的鲁棒性。
希望这个示例能帮助你完成 PMSM 的伺服控制系统仿真!

GitCode 天启AI是一款由 GitCode 团队打造的智能助手,基于先进的LLM(大语言模型)与多智能体 Agent 技术构建,致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话,还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力,真正做到“一句话,让 Al帮你完成复杂任务”。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容









所有评论(0)