shallow wave model

Shallow Water Equation（浅水方程）模型是流体动力学中的经典简化模型，广泛应用于水面波动模拟（如海洋、湖泊、洪水演进），在计算机图形学中常用于实时水体效果。
两个物理假设
浅水条件：流体深度远小于水平尺度（例如湖泊深度 << 湖面宽度），此时垂直方向速度变化可忽略。
静水压力近似：垂直方向压力分布符合静力学平衡（压力随深度线性增加）。

高度场

水波的模拟是通过更新高度场 h(x) 来完成的。u(x)是水平速度矢量。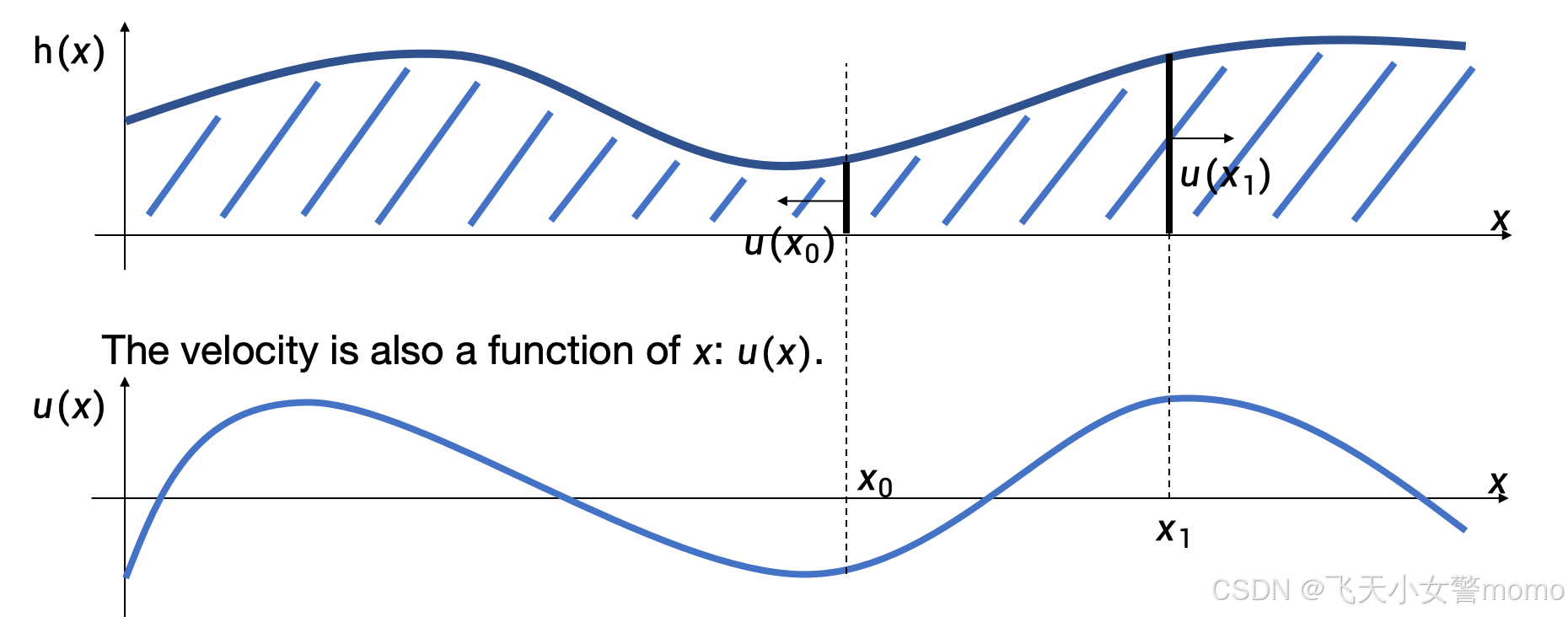

浅水方程的近似

质量守恒要求：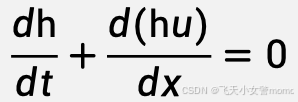

动量守恒要求

忽略对流项和外力项，然后做以下变形

最终得到浅水方程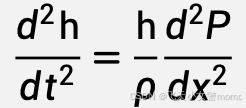

浅水方程的数值化求解

有限差分法 离散化该浅水方程

由此方程可通过当前时刻和上个时刻的高度值，更新下一时刻的高度值。

同时要满足体积守恒

有两种办法

第二种方法直接用常数值H来替代方程中的hi

压强的计算

压强也是高度的函数 $$P_i=\rho g{h}_i$$

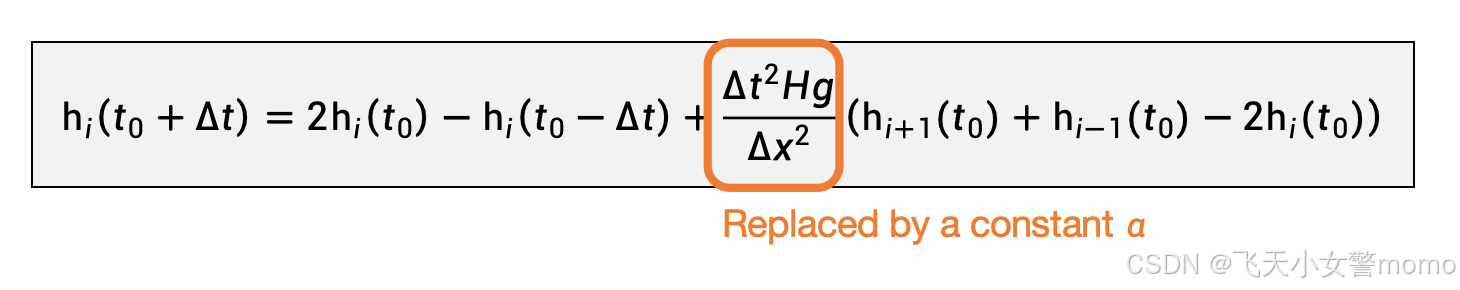
粘滞系数

液体分子之间也有电磁力/摩擦力，用粘滞系数来模拟这一物理现象。
得到最终的浅水方程：

边界条件

Dirichlet 边界条件：设定边界的值为固定常数。

Neumann 边界条件：设定相邻网格点的高度相等，即 $$h_{i+1}\equiv h_i$$

流固耦合

two coupling： 流体对固体的影响；固体对流体的影响。

固体对流体的影响

固体吃水，会排开一部分体积/高度 e，

虚拟高度

在固体位置 i 和 i+1 处，用虚拟高度vi vi+1 来模拟压强，排开这部分水

整理得 泊松方程如下， 其中vi和vi+1是未知量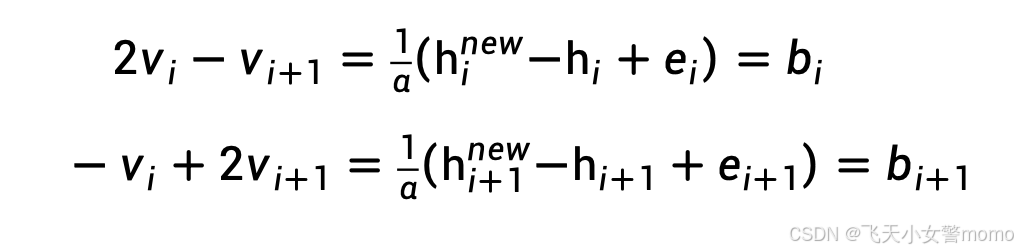

写成矩阵形式

使用共轭梯度求Ax=b。

作业代码实现

带耦合的shollow_wave 函数的实现原理如上个图片展示的那样。浅水方程的更新比较简单。
计算耦合过程中的虚拟高度 vh 要稍微复杂点。

void Shallow_Wave(float[,] old_h, float[,] h, float [,] new_h)
	{		
		//Step 1:
		//TODO: Compute new_h based on the shallow wave model.
		for (int i=0; i<size; i++)
		{
			for (int j=0; j<size; j++)
			{	
				new_h[i,j] = h[i,j] + (h[i,j] - old_h[i,j]) * damping;

				if (i>0)      new_h[i,j] += rate * (h[i-1,j] - h[i,j]);
				if (i<size-1) new_h[i,j] += rate * (h[i+1,j] - h[i,j]);
				if (j>0)      new_h[i,j] += rate * (h[i,j-1] - h[i,j]);
				if (j<size-1) new_h[i,j] += rate * (h[i,j+1] - h[i,j]);
			}
		}
		//Step 2: Block->Water coupling
		//TODO: for block 1, calculate low_h.
		GameObject Cube = GameObject.Find("Cube");
		Vector3 cube_p = Cube.transform.position;
		Mesh cube_mesh = Cube.GetComponent<MeshFilter>().mesh;

		int lower_i = (int)((cube_p.x + 5.0f) * 10) - 3;
		int upper_i = (int)((cube_p.x + 5.0f) * 10) + 3;
		int lower_j = (int)((cube_p.z + 5.0f) * 10) - 3;
		int upper_j = (int)((cube_p.z + 5.0f) * 10) + 3;
		
		Bounds bounds = cube_mesh.bounds;

		for (int i = lower_i - 3; i <= upper_i + 3; i++){
			for (int j = lower_j - 3; j <= upper_j + 3; j++){
				if (i >= 0 && j >= 0 && i < size && j < size){
					Vector3 p = new Vector3(i * 0.1f - size * 0.05f, -11, j * 0.1f - size * 0.05f);
					Vector3 q = new Vector3(i * 0.1f - size * 0.05f, -10, j * 0.1f - size * 0.05f);
					p = Cube.transform.InverseTransformPoint(p);
					q = Cube.transform.InverseTransformPoint(q);

					Ray ray = new Ray(p, q - p);
					float dist = 99999;
					bounds.IntersectRay(ray, out dist);

					low_h[i, j] = -11 + dist;
				}
			}
		}
		//TODO: then set up b and cg_mask for conjugate gradient.
		for (int i = 0; i < size; i++){
			for (int j = 0; j < size; j++)
			{
				if (low_h[i, j] > h[i, j])
				{
					b[i, j] = 0;
					vh[i, j] = 0;
					cg_mask[i, j] = false;
				}
				else
				{
					cg_mask[i, j] = true;
					b[i, j] = (new_h[i, j] - low_h[i, j]) / rate;
				}
			}
		}

		//TODO: Solve the Poisson equation to obtain vh (virtual height).
		Conjugate_Gradient(cg_mask, b, vh, lower_i - 1, upper_i + 1, lower_j - 1, upper_j + 1);

		//TODO: for block 2, calculate low_h.
		GameObject Block = GameObject.Find("Block");
		Vector3 Block_p = Block.transform.position;
		Mesh Block_mesh = Block.GetComponent<MeshFilter>().mesh;

		lower_i = (int)((Block_p.x + 5.0f) * 10) - 3;
		upper_i = (int)((Block_p.x + 5.0f) * 10) + 3;
		lower_j = (int)((Block_p.z + 5.0f) * 10) - 3;
		upper_j = (int)((Block_p.z + 5.0f) * 10) + 3;
		
		bounds = Block_mesh.bounds;

		for (int i = lower_i - 3; i <= upper_i + 3; i++){
			for (int j = lower_j - 3; j <= upper_j + 3; j++){
				if (i >= 0 && j >= 0 && i < size && j < size){
					Vector3 p = new Vector3(i * 0.1f - size * 0.05f, -11, j * 0.1f - size * 0.05f);
					Vector3 q = new Vector3(i * 0.1f - size * 0.05f, -10, j * 0.1f - size * 0.05f);
					p = Block.transform.InverseTransformPoint(p);
					q = Block.transform.InverseTransformPoint(q);

					Ray ray = new Ray(p, q - p);
					float dist = 99999;
					bounds.IntersectRay(ray, out dist);

					low_h[i, j] = -11 + dist;
				}
			}
		}
		//TODO: then set up b and cg_mask for conjugate gradient.
		for (int i = 0; i < size; i++){
			for (int j = 0; j < size; j++)
			{
				if (low_h[i, j] > h[i, j])
				{
					b[i, j] = 0;
					vh[i, j] = 0;
					cg_mask[i, j] = false;
				}
				else
				{
					cg_mask[i, j] = true;
					b[i, j] = (new_h[i, j] - low_h[i, j]) / rate;
				}
			}
		}
		
		Conjugate_Gradient(cg_mask, b, vh, lower_i - 1, upper_i + 1, lower_j - 1, upper_j + 1);

		//TODO: Diminish vh.
		gamma = 0.1f;
		
		//TODO: Update new_h by vh.
		for (int i=0; i<size; i++)
		{
			for (int j=0; j<size; j++)
			{ 
				if (i>0)      new_h[i,j] += rate * gamma * (vh[i-1,j] - vh[i,j]);
				if (i<size-1) new_h[i,j] += rate * gamma * (vh[i+1,j] - vh[i,j]);
				if (j>0)      new_h[i,j] += rate * gamma * (vh[i,j-1] - vh[i,j]);
				if (j<size-1) new_h[i,j] += rate * gamma * (vh[i,j+1] - vh[i,j]);
			}
  		}
		//Step 3
		//TODO: old_h <- h; h <- new_h;
		for (int i = 0; i < size; i++)
		{
			for (int j = 0; j < size; j++)
			{
                old_h[i, j] = h[i, j];
                h[i, j] = new_h[i, j];
            }
		}

		//Step 4: Water->Block coupling.
		//More TODO here.
	}

当按下 r 后，在随机位置（格子）注入一个高度， 并在该格子周围减去这个高度来保持体积恒定。然后通过shallow_wave这个函数更新高度场来形成涟漪。

void Update () 
	{
		Mesh mesh = GetComponent<MeshFilter> ().mesh;
		Vector3[] X    = mesh.vertices;
		float[,] new_h = new float[size, size];
		float[,] h     = new float[size, size];

		//TODO: Load X.y into h.
		for (int i=0; i<size; i++)
		{
			for (int j=0; j<size; j++)
			{	
				h[i,j] = X[i*size+j].y;
			}
		}

		if (Input.GetKeyDown ("r")) 
		{
			//TODO: Add random water.
			int i = UnityEngine.Random.Range(1, size-1);
			int j = UnityEngine.Random.Range(1, size-1);
			
			float r = Random.Range(0.5f, 2.0f);

            h[i, j] += r;
            h[i - 1, j] -= r / 4;
            h[i, j - 1] -= r / 4;
            h[i + 1, j] -= r / 4;
            h[i, j + 1] -= r / 4;
		}

		for(int l=0; l<8; l++)
		{
			Shallow_Wave(old_h, h, new_h);
		}
		//TODO: Store h back into X.y and recalculate normal.
		for (int i=0; i<size; i++)
		{
			for (int j=0; j<size; j++)
			{	
				X[i*size+j].y = h[i,j];
			}
			//Debug.Log(h[i,0]);
		}
		mesh.vertices = X;
		mesh.RecalculateNormals();
	}
}