【机器学习】决策树

在机器学习中，有一种与神经网络并行的非参数化模型——决策树模型及其变种。顾名思义，决策树采用了与树类似的结构。现实中的树是根在下、从下往上生长的，决策树却是根在上，从上往下生长的。但是，两者都有根、枝干的分叉与叶子。本文详细介绍了决策树的构造、ID3算法、C4.5的算法、CART算法以及C4.5算法的详细步骤用Python代码实现。

2401_84149564

990人浏览 · 2025-06-01 03:38:41

2401_84149564 · 2025-06-01 03:38:41 发布

六、动手实现决策树C4.5的算法详解步骤以及Python完整代码实现

一、引言

在机器学习中，有一种与神经网络并行的非参数化模型——决策树模型及其变种。顾名思义，决策树采用了与树类似的结构。现实中的树是根在下、从下往上生长的，决策树却是根在上，从上往下生长的。但是，两者都有根、枝干的分叉与叶子。在决策树中，最上面的节点称为根节点，最下面没有分叉的节点称为叶节点。其中，根节点和内部节点都有一些边指向其他节点，这些被指向的节点就称为它的子节点。叶节点是树的最末端，没有指向其他根节点的边，而除根结点之外，每个内部节点和叶节点都有唯一的节点指向它，该节点称为其父节点。本文详细介绍了决策树的构造、ID3算法、C4.5的算法、CART算法以及C4.5算法的详细步骤用Python代码实现。

二、决策树的构造

1. 决策树的基本概念

决策树是一种非参数监督学习算法，通过将数据集按照特定特征递归地分裂为较小的子集，从而构建出一个预测模型。决策树结构包括：

根节点：代表整个数据集。
内部节点：表示对特征的测试。
分支：表示测试的输出。
叶节点：代表最终的分类结果或回归值。

决策树的构造本质上是一个特征选择和递归划分的过程，目标是构建一个能够最大程度反映数据内在规律的树结构。

2. 决策树构造的基本框架

决策树构造通常遵循"自顶向下、递归分治"的策略，基本算法框架为：

函数 BuildDecisionTree(数据集D, 特征集A, 选择标准criterion):
    创建节点N
    
    # 终止条件
    如果 满足终止条件:
        将N标记为叶节点，赋予类别/值
        返回N
        
    # 选择最优特征
    根据criterion选择最优特征A_best和分割点
    
    # 根据特征分割数据
    将数据集D根据A_best分割为若干子集{D_1, D_2, ..., D_v}
    
    # 递归构建子树
    对于每个子集D_j:
        子树j = BuildDecisionTree(D_j, A - {A_best}, criterion)
        将子树j连接到节点N
        
    返回N

终止条件通常包括：
（1）节点中的样本全部属于同一类别。

（2）特征集为空或样本在所有特征上取值相同。

（3）节点中的样本数小于预定阈值。

三、决策树的ID3算法

1. ID3算法基本原理

ID3(Iterative Dichotomiser 3)算法是由Ross Quinlan在1986年提出的决策树生成算法，它通过信息论中的熵(entropy)和信息增益(information gain)来构建决策树。ID3算法的核心思想是：在每一步构建决策树的过程中，选择能够最大化信息增益的特征作为当前节点的分裂特征。

2. 信息论基础

2.1 熵(Entropy)

熵是信息论中表示随机变量不确定性的度量。对于一个随机变量 $Y$ ，其熵 $H(Y)$ 定义为：

$H(Y) = -\sum_{i=1}^{n} P(y_i) \log_2 P(y_i)$

其中：
$y_i$ 是随机变量 $Y$ 可能的取值。
$P(y_i)$ 是 $y_i$ 出现的概率。
$n$ 是 $Y$ 可能取值的数量。
$\log_2$ 表示以2为底的对数。

在决策树中，对于一个数据集 $D$ ，假设类别标签有 $K$ 个可能取值，第 $k$ 个类别的样本数为 $|C_k|$ ，则数据集 $D$ 的熵为：

$H(D) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|}$

其中 $\frac{|C_k|}{|D|}$ 表示类别 $k$ 在数据集中的占比。

2.2 条件熵(Conditional Entropy)

条件熵 $H(Y|X)$ 表示在已知随机变量 $X$ 的条件下，随机变量 $Y$ 的不确定性：

$H(Y|X) = \sum_{j=1}^{m} P(x_j) H(Y|X=x_j)$

其中：
$x_j$ 是随机变量 $X$ 的可能取值。

$P(x_j)$ 是 $x_j$ 出现的概率。
$H(Y|X=x_j)$ 是在 $X=x_j$ 条件下 $Y$ 的熵。

在决策树中，对于特征 $A$ ，数据集 $D$ 可以划分为 $v$ 个子集 $\{D_1, D_2, ..., D_v\}$ ，则条件熵 $H(D|A)$ 为：

$H(D|A) = \sum_{j=1}^{v} \frac{|D_j|}{|D|} H(D_j)$

其中 $\frac{|D_j|}{|D|}$ 表示子集 $D_j$ 在数据集中的占比。

2.3 信息增益(Information Gain)

信息增益表示由于使用特征$A$划分数据集而导致的不确定性减少量：

$Gain(D, A) = H(D) - H(D|A)$

用公式展开为：

$Gain(D, A) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|} - \left( -\sum_{j=1}^{v} \frac{|D_j|}{|D|} \sum_{k=1}^{K} \frac{|D_j^k|}{|D_j|} \log_2 \frac{|D_j^k|}{|D_j|} \right)$

其中：
$|D_j^k|$ 表示子集 $D_j$ 中属于类别$k$的样本数。

3. ID3算法完整流程

ID3算法采用自顶向下的贪心方法构建决策树，其完整的数学流程如下：

（1）计算当前数据集的熵：

$H(D) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|}$

（2）对每个未使用的特征 $A$ ：
计算条件熵 $H(D|A)$ ：

$H(D|A) = \sum_{j=1}^{v} \frac{|D_j|}{|D|} H(D_j)$

计算信息增益 $Gain(D, A)$ ：

$Gain(D, A) = H(D) - H(D|A)$

（3）选择信息增益最大的特征 $A_{best}$ 作为当前节点的分裂特征：

$A_{best} = \arg\max_{A} Gain(D, A)$

（4）对 $A_{best}$ 的每个可能取值 $a_j$ ：
（1）创建子节点，并将满足 $A_{best} = a_j$ 的样本分配给该子节点。
（2）如果子节点的样本都属于同一类别 $C_k$ ，则将子节点标记为叶节点，类别为 $C_k$ ，
否则，对子节点递归执行步骤1-4。

4. ID3算法的特点与局限性

4.1 特点：
（1）使用信息增益作为特征选择的度量，倾向于选择具有较大信息增益的特征。
（2）构建的决策树通常较为平衡。
（3）计算简单，易于实现。

4.2 局限性：
（1）偏向多值特征：ID3算法中的信息增益度量会偏向于选择取值较多的特征。例如，对于一个唯（2）一标识符特征（如ID），其信息增益会非常高，但对分类几乎没有泛化能力。
（3）无法处理连续值特征：ID3算法只能处理离散值特征，需要对连续值特征进行离散化处理。
（4）无法处理缺失值：没有内置处理缺失值的机制。
（5）容易过拟合：没有剪枝策略，容易生成过于复杂的树。
（6）无法处理不平衡数据：对于类别不平衡的数据集，ID3算法可能会偏向于主要类别。

5. ID3算法的数学推导

ID3算法的关键是选择最优特征，这是通过最大化信息增益实现的。以下是这一过程的数学推导：

假设特征 $A$ 将数据集 $D$ 分割成 $v$ 个子集 $\{D_1, D_2, ..., D_v\}$ ，这些子集的熵可分别计算为：

$H(D_j) = -\sum_{k=1}^{K} \frac{|D_j^k|}{|D_j|} \log_2 \frac{|D_j^k|}{|D_j|}$

其中 $|D_j^k|$ 是子集 $D_j$ 中属于类别 $k$ 的样本数量。

条件熵 $H(D|A)$ 是这些子集熵的加权平均：

$H(D|A) = \sum_{j=1}^{v} \frac{|D_j|}{|D|} H(D_j)$

用具体公式表示为：

$H(D|A) = \sum_{j=1}^{v} \frac{|D_j|}{|D|} \left( -\sum_{k=1}^{K} \frac{|D_j^k|}{|D_j|} \log_2 \frac{|D_j^k|}{|D_j|} \right)$

而信息增益是原始熵与条件熵的差值：

$Gain(D, A) = H(D) - H(D|A)$

展开后：

$Gain(D, A) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|} - \sum_{j=1}^{v} \frac{|D_j|}{|D|} \left( -\sum_{k=1}^{K} \frac{|D_j^k|}{|D_j|} \log_2 \frac{|D_j^k|}{|D_j|} \right)$

6. ID3算法伪代码

函数 ID3(数据集D, 特征集A, 阈值ε):
    创建节点N
    
    # 如果数据集D中所有样本属于同一类别C_k
    如果 D中样本都属于类别C_k:
        将N标记为C_k类叶节点
        返回N
        
    # 如果特征集A为空或数据集D中样本在A上取值相同
    如果 A为空 或 D中样本在A上取值相同:
        将N标记为叶节点，类别为D中样本数最多的类
        返回N
        
    # 否则，计算A中各特征的信息增益，选择信息增益最大的特征A_best
    对于每个特征A_i in A:
        计算信息增益Gain(D, A_i)
    A_best = 信息增益最大的特征
    
    # 如果最大信息增益小于阈值ε，则不再划分
    如果 Gain(D, A_best) < ε:
        将N标记为叶节点，类别为D中样本数最多的类
        返回N
        
    # 以A_best为划分特征构建子树
    将N标记为特征A_best对应的内部节点
    对于A_best的每个可能取值a_j:
        D_j = 满足A_best=a_j的D的子集
        如果 D_j为空:
            创建叶节点N_j，类别为D中样本数最多的类
            将N_j作为N的子节点
        否则:
            调用ID3(D_j, A - {A_best}, ε)获得子树
            将子树作为N的子节点
            
    返回N

7. 一个简单的ID3算法示例

假设我们有一个关于是否去钓鱼的决策问题，特征包括：天气(Outlook)、温度(Temperature)、湿度(Humidity)和刮风(Windy)，类别为是否去钓鱼(PlayTennis)。

假设部分数据如下：

ID3算法会计算每个特征的信息增益。首先计算整个数据集的熵 $H(D)$ ，然后计算各个特征的条件熵 $H(D|A)$ ，最后得到信息增益 $Gain(D,A)$ 。

比如，对于特征"Outlook"，它有三个可能取值：Sunny、Overcast和Rain，会将数据集分成三个子集。计算这三个子集对应的熵，再根据子集大小计算加权平均，得到条件熵 $H(D|Outlook)$ 。

最终，ID3算法会选择信息增益最大的特征作为根节点，在这个例子中很可能是"Outlook"。然后对每个子集递归应用这个过程，直到所有叶节点都包含单一类别的样本或满足其他停止条件。

这种基于信息熵的方法使得ID3算法能够有效地学习决策规则，为后续的C4.5、C5.0和CART等更先进的决策树算法奠定了基础。

四、决策树的C4.5算法

1. C4.5算法简介

C4.5算法是Ross Quinlan在1993年提出的决策树算法，是ID3算法的改进版本。C4.5解决了ID3的诸多限制，包括处理连续特征、处理缺失值以及通过后剪枝避免过拟合等问题，使其成为机器学习领域最经典的决策树算法之一。

2. C4.5的核心改进

2.1 信息增益率

ID3使用信息增益作为特征选择标准，但这会偏向于取值较多的特征。C4.5引入了信息增益率来解决这个问题：

$GainRatio(D, A) = \frac{Gain(D, A)}{SplitInfo(D, A)}$

其中分裂信息(Split Information)计算公式为：

$SplitInfo(D, A) = -\sum_{j=1}^{v} \frac{|D_j|}{|D|} \log_2 \frac{|D_j|}{|D|}$

分裂信息实际上度量了特征A对数据集D的分裂程度。对于取值较多的特征，其分裂信息通常较大，通过除以分裂信息，信息增益率能平衡对多值特征的偏好。

2.2 连续特征处理

C4.5能处理连续型特征，其方法是：

（1）对特征A的所有不同取值进行排序： $a_1 < a_2 < ... < a_m$ 。
（2）找出所有可能的分裂点： $t = \frac{a_i + a_{i+1}}{2}$ ，共有m-1个。
（3）对每个候选分裂点t，根据A≤t与A>t将数据集分成两部分。
（4）计算每个分裂点t的信息增益率。
（5）选择信息增益率最高的分裂点作为最终分裂方式。

数学表达式为：
$Gain(D, A, t) = H(D) - \left[ \frac{|D_{A \leq t}|}{|D|} H(D_{A \leq t}) + \frac{|D_{A > t}|}{|D|} H(D_{A > t}) \right]$

$SplitInfo(D, A, t) = -\frac{|D_{A \leq t}|}{|D|} \log_2 \frac{|D_{A \leq t}|}{|D|} - \frac{|D_{A > t}|}{|D|} \log_2 \frac{|D_{A > t}|}{|D|}$

$GainRatio(D, A, t) = \frac{Gain(D, A, t)}{SplitInfo(D, A, t)}$

2.3 缺失值处理

C4.5能够优雅地处理缺失值，主要通过两种机制：

（1）计算信息增益时：只使用在特征A上有值的样本子集 $\tilde{D}$ 计算信息增益，然后按比例放大：

$Gain(D, A) = \frac{|\tilde{D}|}{|D|} \times \left[ H(\tilde{D}) - \sum_{j=1}^{v} \frac{|\tilde{D}_j|}{|\tilde{D}|} H(\tilde{D}_j) \right]$

（2）分类决策时：当遇到缺失特征值的样本时，C4.5将其权重按照各分支样本比例分配到所有子节点，实现概率性分类。

2.4 后剪枝策略

C4.5采用基于错误率的后剪枝(Error-Based Pruning)，其步骤为：

（1）先构建完整决策树。
（2）自下而上遍历非叶节点。
（3）计算每个节点的悲观错误率估计。

对于包含N个样本的节点，其中E个样本分类错误，悲观错误率估计为：

$\hat{e} = \frac{E + \frac{z^2}{2} + z\sqrt{\frac{E(N-E)}{N} + \frac{z^2}{4N}}}{N + z^2}$

其中z通常取0.69，对应75%的置信度。如果将节点替换为叶节点后悲观错误率不增加，则进行剪枝。

3. C4.5算法完整流程

3.1 构建决策树的伪代码：

函数 BuildC45Tree(数据集D, 特征集A):
    创建节点N
    
    # 终止条件
    如果 D中样本都属于同一类别C:
        将N标记为C类叶节点
        返回N
    如果 A为空 或 D中样本在A上取值相同:
        将N标记为叶节点，类别为D中样本最多的类
        返回N
        
    # 计算特征的信息增益率
    对于每个特征A_i in A:
        如果A_i是离散特征:
            计算GainRatio(D, A_i)
        如果A_i是连续特征:
            找出最佳分裂点t_i
            计算GainRatio(D, A_i, t_i)
    
    选择信息增益率最大的特征A_best作为划分特征
    将N标记为特征A_best对应的内部节点
    
    如果A_best是离散特征:
        对于A_best的每个可能取值a_j:
            创建一个分支
            D_j = 满足A_best=a_j的样本子集
            如果D_j为空:
                创建叶节点，类别为D中样本最多的类
            否则:
                递归调用BuildC45Tree(D_j, A - {A_best})
    
    如果A_best是连续特征:
        找到最佳分裂点t_best
        创建两个分支A_best ≤ t_best和A_best > t_best
        D_left = 满足A_best ≤ t_best的样本子集
        D_right = 满足A_best > t_best的样本子集
        递归调用BuildC45Tree(D_left, A)
        递归调用BuildC45Tree(D_right, A)
    
    返回N

3.2 后剪枝伪代码：

函数 Prune(节点N, 数据集D):
    如果N是叶节点:
        返回N的悲观错误率估计
        
    记录N的子树错误率估计 = 0
    对于N的每个子节点N_i和对应的数据子集D_i:
        子树错误率估计 += Prune(N_i, D_i)
    
    计算N作为叶节点的悲观错误率估计
    
    如果(N作为叶节点的错误率) ≤ 子树错误率估计:
        将N转换为叶节点，类别为D中样本最多的类
        返回N作为叶节点的错误率
    否则:
        返回子树错误率估计

4. C4.5的数学基础

4.1 信息熵

信息熵衡量数据集的纯度：

$H(D) = -\sum_{k=1}^{K} p_k \log_2 p_k$

其中 $p_k$ 是第k类样本的比例。

4.2 条件熵

条件熵衡量已知特征A的情况下数据集D的不确定性：

$H(D|A) = \sum_{j=1}^{v} \frac{|D_j|}{|D|} H(D_j)$

4.3 信息增益

信息增益表示使用特征A划分带来的不确定性减少：

$Gain(D, A) = H(D) - H(D|A)$

展开公式：

$Gain(D, A) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|} + \sum_{j=1}^{v} \frac{|D_j|}{|D|} \sum_{k=1}^{K} \frac{|D_j^k|}{|D_j|} \log_2 \frac{|D_j^k|}{|D_j|}$

其中 $|D_j^k|$ 表示特征A取第j个值且类别为k的样本数量。

5. C4.5的优缺点

5.1 优点
（1）使用信息增益率克服了ID3偏向多值特征的缺点。
（2）能够处理连续特征。
（3）能够处理缺失值。
（4）使用后剪枝避免过拟合。
（5）生成的规则易于理解和解释。

5.2 缺点
（1）对噪声敏感。
（2）对于不平衡数据集效果欠佳。
（3）小数据集上容易过拟合。
（4）无法处理回归问题。
（5）构建的树可能不是全局最优。

6. C4.5与ID3决策树的比较

C4.5算法是决策树算法发展的重要里程碑，为后续的C5.0和随机森林等算法奠定了基础。虽然现在有更先进的算法，C4.5依然是理解决策树的重要起点，其核心思想在当代机器学习中。

五、决策树的CART算法

1. 基本原理与特点

CART(Classification And Regression Trees)是由Leo Breiman等人在1984年提出的决策树算法，具有以下关键特点：

（1）双重功能：既可用于分类问题，也可用于回归问题。
（2）二叉树结构：每个内部节点总是将数据分成两个子集，形成二叉树。
（3）分裂准则：分类问题使用基尼指数(Gini Index)，回归问题使用均方误差(MSE)。
（4）剪枝方法：使用代价复杂度剪枝(Cost-Complexity Pruning)。
（5）处理能力：可同时处理连续特征和离散特征，能处理缺失值。

CART算法不使用信息增益或增益率，而是追求"最纯"的子节点，通过递归二分来构建决策树。

2. CART分类树

2.1 基尼指数(Gini Index)

CART分类树使用基尼指数来衡量数据集的不纯度。基尼指数反映了从数据集中随机抽取两个样本，其类别标签不一致的概率。

数据集D的基尼指数定义为：

$Gini(D) = 1 - \sum_{k=1}^{K} \left(\frac{|C_k|}{|D|}\right)^2$

其中：
K是类别的数量

$|C_k|$ 是第k类样本的数量
$|D|$ 是数据集的总样本数

基尼指数越小，数据集的纯度越高。当所有样本都属于同一类别时， $Gini(D) = 0$ 。

2.2 特征选择与分裂

CART采用二分法，对于每个特征A：

（1）对于离散特征：考虑所有可能的二分方案，将特征的取值集合分成两个互斥的子集。
（2 ）对于连续特征：考虑所有可能的分裂点，将数据分成 ≤ 和 > 两部分。

对于特征A和分裂点s，分裂后的基尼指数计算为：

$Gini(D, A, s) = \frac{|D_1|}{|D|} Gini(D_1) + \frac{|D_2|}{|D|} Gini(D_2)$

其中：
$D_1$ 是满足分裂条件的样本集合（如A ≤ s或A ∈ subset1）
$D_2$ 是不满足分裂条件的样本集合（如A > s或A ∈ subset2）

CART选择使分裂后基尼指数最小的特征和分裂点作为最优分裂方案：

$\{A^*, s^*\} = \arg\min_{A,s} Gini(D, A, s)$

2.3 二元分类的简化计算

对于二元分类问题，若正类样本比例为p，则基尼指数可简化为：

$Gini(D) = 1 - p^2 - (1-p)^2 = 2p(1-p)$

3. CART回归树

3.1 平方误差最小化原则

CART回归树采用平方误差最小化准则，目标是使划分后的数据子集中的样本输出值波动最小。

对于数据集D，其输出值的方差可表示为：

$Var(D) = \frac{1}{|D|} \sum_{i=1}^{|D|} (y_i - \bar{y})^2$

其中：
$y_i$ 是第i个样本的真实输出值
$\bar{y}$ 是数据集D中所有样本输出值的平均值

3.2 特征选择与分裂

对于特征A和分裂点s，分裂后的平方误差为：

$MSE(D, A, s) = \frac{|D_1|}{|D|} Var(D_1) + \frac{|D_2|}{|D|} Var(D_2)$

或者等价地表示为：

$MSE(D, A, s) = \frac{1}{|D|} \left[ \sum_{x_i \in D_1} (y_i - c_1)^2 + \sum_{x_j \in D_2} (y_j - c_2)^2 \right]$

其中：
$c_1$ 是子集 $D_1$ 中样本输出值的平均值
$c_2$ 是子集 $D_2$ 中样本输出值的平均值

CART选择使平方误差最小的特征和分裂点：

$\{A^*, s^*\} = \arg\min_{A,s} MSE(D, A, s)$

3.3 预测值确定

对于回归树的每个叶节点t，其预测值$c_t$为该节点所有样本输出值的平均：

$c_t = \frac{1}{|D_t|} \sum_{x_i \in D_t} y_i$

4. 特征处理方法

4.1 连续特征处理

对于连续特征A：

（1）对特征值排序： $a_1, a_2, ..., a_m$ 。
（2）考虑所有可能的分裂点： $s_i = \frac{a_i + a_{i+1}}{2}$ ，共m-1个。
（3）.对每个分裂点计算分裂后的基尼指数或MSE。
（4）选择最优分裂点。

4.2 离散特征处理

对于取值集合为 $\{a_1, a_2, ..., a_m\}$ 的离散特征A：

（1）考虑所有可能的二分方案，将取值集合分成两个互斥的子集 $A_1$ 和 $A_2$ 。
（2）共有 $2^{m-1}-1$ 种可能的二分方案。
（3）对每种方案计算分裂后的基尼指数或MSE。
（4）选择最优二分方案。

4.3 缺失值处理

CART使用替代分裂(Surrogate Split)处理缺失值：

（1）对于最优分裂特征上有缺失值的样本，寻找与最优分裂规则最相关的替代特征。
（2）计算每个替代特征的相关性，选择相关性最高的特征。
（3）使用替代特征对缺失值样本进行分类。

5. 代价复杂度剪枝(Cost-Complexity Pruning)

CART使用代价复杂度剪枝算法，其步骤为：

5.1 定义代价复杂度函数

对于子树 $T$ ，定义代价复杂度为：

$C_\alpha(T) = R(T) + \alpha |T|$

其中：
$R(T)$ 是子树 $T$ 的预测误差（分类树为错误率，回归树为均方误差）。
$|T|$ 是子树 $T$ 的叶节点数量。
$\alpha$ 是复杂度参数，控制树的复杂度和拟合程度的权衡。

5.2 剪枝过程

（1）构建完整树：首先构建一个完整的决策树$T_0$，直到每个叶节点都纯净或满足停止条件
（2）生成嵌套子树序列：
从 $T_0$ 开始，计算每个内部节点的代价变化率 $\alpha$ 。
对于节点t，将其子树替换为叶节点的代价变化率为：
$\alpha_t = \frac{R(t) - R(T_t)}{|T_t| - 1}$
选择 $\alpha$ 值最小的节点进行剪枝，生成新的子树。
重复此过程，直到只剩根节点，形成嵌套子树序列 $T_0 > T_1 > ... > T_n$ 。
（3）选择最优子树：
使用独立验证集或交叉验证评估每棵子树的性能
选择测试误差最小的子树作为最终模型

6. CART与ID3/C4.5的比较

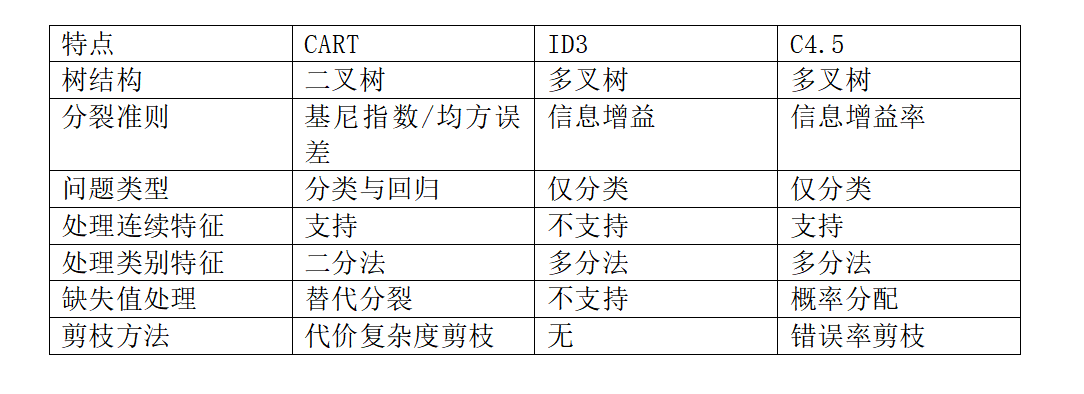
7. CART的优缺点

7.1 优点

（1）灵活性：既可用于分类也可用于回归。
（2）鲁棒性：对异常值不敏感。
（3）可解释性：决策逻辑清晰直观。
（4）处理能力：可处理混合类型特征，包括连续和离散特征。
（5）缺失值处理：通过替代分裂有效处理缺失值。
（6）特征选择：可识别重要特征。

7.2 缺点

（1）不稳定性：小的数据变化可能导致树结构显著变化。
（2）局部最优：贪心算法无法保证全局最优解。
（3）偏向：倾向于选择取值较多的特征。
（4）复杂关系：难以表达复杂的特征关系。
（5）过拟合风险：需要适当的剪枝策略。

8. CART算法的实现与优化技巧

8.1 停止条件设置

合理设置停止条件避免过拟合：
（1）节点样本数小于阈值。
（2）节点深度达到最大值。
（3）分裂后不纯度降低小于阈值。
（4）子节点样本数小于阈值。

8.2 参数调优

关键参数包括：
（1）最大树深度。
（2）最小样本分裂数。
（3）最小叶节点样本数。
（4）复杂度参数α。

8.3 集成方法

CART树常作为集成方法的基学习器：
（1）随机森林：构建多棵随机化的CART树。
（2）梯度提升树(GBDT)：序列化构建CART树。
（3）XGBoost/LightGBM：优化的GBDT实现

8.4 特征工程

（1）处理高维特征空间。
（2）转换高基数类别特征。
（3）创建交互特征增强表达能力。

9. 实际应用中的CART

CART因其灵活性和可解释性在许多领域得到广泛应用：

（1）金融：信用评估、风险分析。
（2）医疗：疾病诊断、预后预测。
（3）营销：客户细分、购买行为预测。
（4）环境：污染分析、生态系统建模。

使用CART的最佳实践包括：
（1）适当的预处理，包括处理异常值和缺失值。
（2）通过交叉验证仔细调节参数。
（3）结合正则化技术控制过拟合。
（4）考虑与其他模型集成以提高性能。

CART算法作为决策树家族中的重要成员，通过其独特的二分法和代价复杂度剪枝，以及处理分类与回归问题的能力，在机器学习领域占据重要地位，同时也为随机森林和梯度提升等现代集成方法奠定了基础。

六、动手实现决策树C4.5的算法详解步骤以及Python完整代码实现

（一）随机生成数据集到指定的文件中。

（二）决策树C4.5的算法步骤。

1. 算法基本原理

C4.5算法是ID3算法的改进版，主要通过引入信息增益率来解决ID3倾向于选择取值较多的特征的问题。该实现包含以下关键部分：

1.1 数据预处理
处理连续特征通过等分为10个区间
将离散特征转换为整数编码
将缺失值用-1表示
实现80/20的训练集和测试集划分

1.2 核心数据结构
Node`类用于表示决策树的节点
DecisionTree`类实现决策树的构建和预测

2. 信息论基础与数学公式

2.1 信息熵(Entropy)
信息熵表示随机变量不确定性的度量：

$H(Y) = -\sum_{i=1}^{n} P(y_i) \log_2 P(y_i)$

Python代码实现：

def entropy(self, Y):
    cnt = np.unique(Y, return_counts=True)[1]  # 统计每个类别出现的次数
    N = len(Y)
    ent = -np.sum([self.aloga(Ni / N) for Ni in cnt])
    return ent

2.2 信息增益(Information Gain)
信息增益表示使用特征X对数据集划分前后熵的减少量：

$IG(Y, X) = H(Y) - H(Y|X)$

其中H(Y|X)是条件熵，计算公式为：

$H(Y|X) = \sum_{j=1}^{v} \frac{|X_j|}{|X|} H(Y|X=X_j)$

Python代码实现：

def info_gain(self, X, Y, feat, val):
    # 划分前的熵
    N = len(Y)
    if N == 0:
        return 0
    HX = self.entropy(Y)
    HXY = 0 # H(X|Y)
    # 分别计算H(X|X_F<=val)和H(X|X_F>val)
    Y_l = Y[X[:, feat] <= val]
    HXY += len(Y_l) / len(Y) * self.entropy(Y_l)
    Y_r = Y[X[:, feat] > val]
    HXY += len(Y_r) / len(Y) * self.entropy(Y_r)
    return HX - HXY

2.3 特征的分裂信息(Split Information)
特征X的分裂信息衡量了特征X本身的熵：

$SplitInfo(X) = -\sum_{j=1}^{v} \frac{|X_j|}{|X|} \log_2 \frac{|X_j|}{|X|}$

Python代码实现：

def entropy_YX(self, X, Y, feat, val):
    HYX = 0
    N = len(Y)
    if N == 0:
        return 0
    Y_l = Y[X[:, feat] <= val]
    HYX += -self.aloga(len(Y_l) / N)
    Y_r = Y[X[:, feat] > val]
    HYX += -self.aloga(len(Y_r) / N)
    return HYX

2.4 信息增益率(Information Gain Ratio)
信息增益率是C4.5算法的核心，它将信息增益除以分裂信息，避免偏向多值特征：

$GainRatio(Y, X) = \frac{IG(Y, X)}{SplitInfo(X)}$

Python代码实现：

def info_gain_ratio(self, X, Y, feat, val):
    IG = self.info_gain(X, Y, feat, val)
    HYX = self.entropy_YX(X, Y, feat, val)
    if HYX == 0:
        return 0
    return IG / HYX

3. 决策树构建过程

3.1 ID3核心算法
决策树构建采用递归方式，遵循以下步骤：
1. 若当前节点样本属于同一类别，将节点标记为叶节点
2. 计算每个特征的每个可能分裂点的信息增益率
3. 选择信息增益率最大的特征和分裂点
4. 计算分裂前后的代价函数变化
5. 若分裂能降低代价，则执行分裂；否则将节点标记为叶节点

3.2 代价函数和正则化
代码中引入了代价函数来控制树的生长：

$Cost(node) = |Y_{node}| \cdot H(Y_{node}) + \lambda$

分裂后的代价为：

$Cost(split) = |Y_{left}| \cdot H(Y_{left}) + |Y_{right}| \cdot H(Y_{right}) + 2\lambda$

其中λ是正则化参数，控制树的复杂度。只有当分裂后的代价小于当前代价时才执行分裂：

Python代码如下：

# 当前代价
cur_cost = len(Y) * self.entropy(Y) + self.lbd
# 分裂后的代价
new_cost = len(new_Y_l) * self.entropy(new_Y_l) + len(new_Y_r) * self.entropy(new_Y_r) + 2 * self.lbd

4. 模型评估与新增功能

4.1 混淆矩阵
对二分类问题，混淆矩阵包含：
真正例(TP)：实际为正，预测为正
真负例(TN)：实际为负，预测为负
假正例(FP)：实际为负，预测为正
假负例(FN)：实际为正，预测为负

基于混淆矩阵计算：
精确率： $Precision = \frac{TP}{TP+FP}$
召回率： $Recall = \frac{TP}{TP+FN}$
F1分数： $F1 = \frac{2 \cdot Precision \cdot Recall}{Precision + Recall}$

4.2 ROC曲线与AUC
ROC曲线绘制了不同阈值下真正例率(TPR)和假正例率(FPR)的关系：
TPR = TP/(TP+FN)（真正例率=召回率）

FPR = FP/(FP+TN)（假正例率）

AUC是ROC曲线下的面积，反映了模型的整体性能。

4.3 特征重要性
特征重要性通过特征在树中被选为分裂点的频率来衡量：
Python代码如下：

def feature_importance(self):
    importance = np.zeros(len(feat_names))
    self._calc_importance(self.root, importance)
    # 归一化
    if np.sum(importance) > 0:
        importance = importance / np.sum(importance)
    return importance

4.4 交叉验证
K折交叉验证通过将数据分成K份，每次使用K-1份训练、1份测试，最后取平均结果：
Python代码如下：

def cross_validation(X, Y, feat_ranges, k=5, lbd=1.0):
    from sklearn.model_selection import KFold
    kf = KFold(n_splits=k, shuffle=True, random_state=42)
    accuracies = []
    # ...训练和评估过程
    return np.mean(accuracies)

4.5 学习曲线
学习曲线通过绘制不同训练集大小下的训练和测试准确率，反映模型随样本量变化的性能：
Python代码如下：

def plot_learning_curve(X, Y, feat_ranges, test_size=0.2, max_samples=None, step=50):
    # ...训练不同大小样本集的模型
    plt.plot(train_sizes, train_scores, 'o-', color='r', label='训练集准确率')
    plt.plot(train_sizes, test_scores, 'o-', color='g', label='测试集准确率')

5. 实现特点与创新

5.1 二分划分策略
本实现采用二分划分策略处理连续特征和离散特征：对于特征X和分裂值val，将数据分成X<=val和X>val两部分。

5.2 预剪枝技术
通过代价函数实现预剪枝，避免过拟合：
Python代码如下：

if new_cost <= cur_cost:
    # 执行分裂...
else:
    # 将当前节点标记为叶节点

功能扩展
添加了多种评估和分析功能：
特征重要性分析
混淆矩阵和精确率/召回率计算
ROC曲线和AUC计算
交叉验证
学习曲线
决策树可视化
模型保存和加载

6. 与sklearn的比较

代码中实现了与sklearn的决策树算法的比较：
sklearn的entropy criterion对应C4.5算法
sklearn的gini criterion对应CART算法

通过比较准确率，可以评估自定义实现的性能。

（三）Python完整代码实现

随机生成数据集的完整Python代码如下：

import pandas as pd
import numpy as np
import os

# 创建目录（如果不存在）
if not os.path.exists('titanic'):
    os.makedirs('titanic')

# 设置随机种子，确保结果可复现
np.random.seed(42)

# 生成样本数量
n_samples = 891  # 与原始Titanic数据集大小相同

# 生成乘客ID
passenger_ids = np.arange(1, n_samples + 1)

# 生成存活情况（0表示未存活，1表示存活）
# 实际Titanic数据集中大约38%的乘客存活
survived = np.random.binomial(1, 0.38, n_samples)

# 生成船票等级（1, 2, 3）
# 设置各等级的概率
pclass_probs = [0.24, 0.21, 0.55]  # 一等舱、二等舱、三等舱的比例
pclass = np.random.choice([1, 2, 3], size=n_samples, p=pclass_probs)

# 生成性别数据
# 设置男性的概率为0.65
sex = np.random.choice(['male', 'female'], size=n_samples, p=[0.65, 0.35])

# 生成年龄数据
# 年龄分布在0.5到80之间，平均为30岁，有一些缺失值
age = np.random.normal(30, 14, n_samples)
age = np.clip(age, 0.5, 80)
# 大约20%的年龄数据缺失
missing_age_indices = np.random.choice(range(n_samples), size=int(n_samples * 0.2), replace=False)
age[missing_age_indices] = np.nan

# 生成兄弟姐妹/配偶人数
sibsp_probs = [0.68, 0.24, 0.06, 0.01, 0.005, 0.005]  # 0, 1, 2, 3, 4, 5+的比例
sibsp = np.random.choice(range(6), size=n_samples, p=sibsp_probs)

# 生成父母/子女人数
parch_probs = [0.76, 0.12, 0.08, 0.02, 0.01, 0.01]  # 0, 1, 2, 3, 4, 5+的比例
parch = np.random.choice(range(6), size=n_samples, p=parch_probs)

# 生成票价数据
# 票价基于船票等级，一等舱最贵，三等舱最便宜
fare = np.zeros(n_samples)
fare[pclass == 1] = np.random.uniform(30, 512, sum(pclass == 1))
fare[pclass == 2] = np.random.uniform(10, 73, sum(pclass == 2))
fare[pclass == 3] = np.random.uniform(0, 69, sum(pclass == 3))

# 生成船舱号
cabins = []
deck_letters = ['A', 'B', 'C', 'D', 'E', 'F', 'G']

for p in pclass:
    if np.random.random() > 0.77:  # 约77%的船舱数据缺失
        cabins.append(np.nan)
    else:
        # 一等舱客户更可能在上层甲板
        if p == 1:
            deck = np.random.choice(deck_letters[:3])
        elif p == 2:
            deck = np.random.choice(deck_letters[2:5])
        else:
            deck = np.random.choice(deck_letters[4:])

        cabin_number = np.random.randint(1, 140)
        cabins.append(f"{deck}{cabin_number}")

# 生成登船港口
embarked_probs = [0.72, 0.08, 0.18, 0.02]  # S, C, Q, 缺失值的比例
embarked = np.random.choice(['S', 'C', 'Q', np.nan], size=n_samples, p=embarked_probs)

# 生成姓名
first_names_male = ['John', 'William', 'James', 'Charles', 'George', 'Thomas', 'Henry', 'Edward', 'Joseph', 'Richard']
first_names_female = ['Mary', 'Anna', 'Elizabeth', 'Margaret', 'Emma', 'Florence', 'Sarah', 'Alice', 'Martha', 'Ellen']
last_names = ['Smith', 'Johnson', 'Williams', 'Brown', 'Jones', 'Miller', 'Davis', 'Wilson', 'Anderson', 'Taylor',
              'Moore', 'Thomas', 'Jackson', 'White', 'Harris', 'Martin', 'Thompson', 'Young', 'Walker', 'Allen']

names = []
for i in range(n_samples):
    last_name = np.random.choice(last_names)
    if sex[i] == 'male':
        first_name = np.random.choice(first_names_male)
        # 添加一些敬称
        title = np.random.choice(['Mr.', 'Dr.', 'Rev.', 'Major.', 'Col.', 'Capt.'],
                                 p=[0.9, 0.02, 0.02, 0.02, 0.02, 0.02])
    else:
        first_name = np.random.choice(first_names_female)
        # 添加一些敬称
        title = np.random.choice(['Mrs.', 'Miss.', 'Ms.', 'Dr.', 'Lady.'], p=[0.5, 0.4, 0.05, 0.03, 0.02])

    names.append(f"{last_name}, {title} {first_name}")

# 生成船票号
tickets = []
for i in range(n_samples):
    ticket_format = np.random.choice([1, 2, 3], p=[0.3, 0.5, 0.2])

    if ticket_format == 1:
        # 简单数字格式
        ticket = str(np.random.randint(10000, 400000))
    elif ticket_format == 2:
        # 带前缀的格式
        prefix = np.random.choice(['PC', 'CA', 'A/5', 'SOTON', 'STON', 'PP', 'SC', 'WC', 'FC'])
        ticket = f"{prefix} {np.random.randint(1000, 100000)}"
    else:
        # 带连字符的格式
        ticket = f"{np.random.randint(10000, 400000)}"

    tickets.append(ticket)

# 创建数据集
titanic_data = pd.DataFrame({
    'PassengerId': passenger_ids,
    'Survived': survived,
    'Pclass': pclass,
    'Name': names,
    'Sex': sex,
    'Age': age,
    'SibSp': sibsp,
    'Parch': parch,
    'Ticket': tickets,
    'Fare': fare,
    'Cabin': cabins,
    'Embarked': embarked
})

# 更新存活率以反映现实数据中的模式
# 例如：男性生存率低，女性生存率高；一等舱乘客生存率高于三等舱
# 身份：女性和孩子优先
titanic_data.loc[(titanic_data['Sex'] == 'female') | (titanic_data['Age'] < 14), 'Survived'] = np.random.binomial(1,
                                                                                                                  0.7,
                                                                                                                  sum((
                                                                                                                                  titanic_data[
                                                                                                                                      'Sex'] == 'female') | (
                                                                                                                                  titanic_data[
                                                                                                                                      'Age'] < 14)))
# 船票等级影响：一等舱生存率高
titanic_data.loc[titanic_data['Pclass'] == 1, 'Survived'] = np.random.binomial(1, 0.6, sum(titanic_data['Pclass'] == 1))
# 年龄影响：老人生存率低
titanic_data.loc[titanic_data['Age'] > 60, 'Survived'] = np.random.binomial(1, 0.25, sum(titanic_data['Age'] > 60))
# 男性生存率低
titanic_data.loc[titanic_data['Sex'] == 'male', 'Survived'] = np.random.binomial(1, 0.2,
                                                                                 sum(titanic_data['Sex'] == 'male'))

# 保存到CSV文件
titanic_data.to_csv('titanic/train.csv', index=False)

print("数据已成功生成并保存到 titanic/train.csv")
print(f"生成的数据包含 {n_samples} 条记录")

决策树C4.5算法的完整Python代码如下：

print('动手实现C4.5算法的决策树')
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 读取数据
data = pd.read_csv('titanic/train.csv')
# 查看具体信息和前五行具体内容，其中NaN代表数据缺失
print(data.info())
print(data[:5])

# 删去编号、姓名、船票编号3列
data.drop(columns=['PassengerId', 'Name', 'Ticket'], inplace=True)

feat_ranges = {}
cont_feat = ['Age', 'Fare']  # 连续特征
bins = 10  # 分类点数

for feat in cont_feat:
    # 数据集中存在缺省值nan，需要用np.nanmin和np.nanmax
    min_val = np.nanmin(data[feat])
    max_val = np.nanmax(data[feat])
    feat_ranges[feat] = np.linspace(min_val, max_val, bins).tolist()
    print(feat, ': ')  # 查看分类点
    for spt in feat_ranges[feat]:
        print(f'{spt:.4f}')

# 只有有限取值的离散特征
cat_feat = ['Sex', 'Pclass', 'SibSp', 'Parch', 'Cabin', 'Embarked']
for feat in cat_feat:
    data[feat] = data[feat].astype('category')  # 数据格式转为分类格式
    print(f'{feat}: {data[feat].cat.categories}')  # 查看类别
    data[feat] = data[feat].cat.codes.to_list()  # 将类别按顺序转换为整数
    ranges = list(set(data[feat]))
    ranges.sort()
    feat_ranges[feat] = ranges

# 将所有缺省值替换为-1
data.fillna(-1, inplace=True)
for feat in feat_ranges.keys():
    feat_ranges[feat] = [-1] + feat_ranges[feat]

# 划分训练集与测试集
np.random.seed(0)
feat_names = data.columns[1:]
label_name = data.columns[0]
# 重排下标之后，按新的下标索引数据
data = data.reindex(np.random.permutation(data.index))
ratio = 0.8
split = int(ratio * len(data))
train_x = data[:split].drop(columns=['Survived']).to_numpy()
train_y = data['Survived'][:split].to_numpy()
test_x = data[split:].drop(columns=['Survived']).to_numpy()
test_y = data['Survived'][split:].to_numpy()
print('训练集大小：', len(train_x))
print('测试集大小：', len(test_x))
print('特征数：', train_x.shape[1])


# 定义结点类
class Node:

    def __init__(self):
        # 内部结点的feat表示用来分类的特征编号，其数字与数据中的顺序对应
        # 叶结点的feat表示该结点的分类结果
        self.feat = None
        # 分类值列表，表示按照其中的值向子结点分类
        self.split = None
        # 子结点列表，叶结点的child为空
        self.child = []


# 定义决策树
class DecisionTree:

    def __init__(self, X, Y, feat_ranges, lbd):
        self.root = Node()
        self.X = X
        self.Y = Y
        self.feat_ranges = feat_ranges  # 特征取值范围
        self.lbd = lbd  # 正则化约束强度
        self.eps = 1e-8  # 防止数学错误log(0)和除以0
        self.T = 0  # 记录叶结点个数
        self.ID3(self.root, self.X, self.Y)

    # 工具函数，计算 a * log a
    def aloga(self, a):
        return a * np.log2(a + self.eps)

    # 计算某个子数据集的熵
    def entropy(self, Y):
        cnt = np.unique(Y, return_counts=True)[1]  # 统计每个类别出现的次数
        N = len(Y)
        ent = -np.sum([self.aloga(Ni / N) for Ni in cnt])
        return ent

    # 计算用feat <= val划分数据集的信息增益
    def info_gain(self, X, Y, feat, val):
        # 划分前的熵
        N = len(Y)
        if N == 0:
            return 0
        HX = self.entropy(Y)
        HXY = 0  # H(X|Y)
        # 分别计算H(X|X_F<=val)和H(X|X_F>val)
        Y_l = Y[X[:, feat] <= val]
        HXY += len(Y_l) / len(Y) * self.entropy(Y_l)
        Y_r = Y[X[:, feat] > val]
        HXY += len(Y_r) / len(Y) * self.entropy(Y_r)
        return HX - HXY

    # 计算特征feat <= val本身的复杂度H_Y(X)
    def entropy_YX(self, X, Y, feat, val):
        HYX = 0
        N = len(Y)
        if N == 0:
            return 0
        Y_l = Y[X[:, feat] <= val]
        HYX += -self.aloga(len(Y_l) / N)
        Y_r = Y[X[:, feat] > val]
        HYX += -self.aloga(len(Y_r) / N)
        return HYX

    # 计算用feat <= val划分数据集的信息增益率
    def info_gain_ratio(self, X, Y, feat, val):
        IG = self.info_gain(X, Y, feat, val)
        HYX = self.entropy_YX(X, Y, feat, val)
        if HYX == 0:
            return 0
        return IG / HYX

    # 用ID3算法递归分类结点，构造决策树
    def ID3(self, node, X, Y):
        # 判断是否已经分类完成
        if len(np.unique(Y)) == 1:
            node.feat = Y[0]
            self.T += 1
            return

        # 寻找最优分类特征和分类点
        best_IGR = 0
        best_feat = None
        best_val = None
        for feat in range(len(feat_names)):
            for val in self.feat_ranges[feat_names[feat]]:
                IGR = self.info_gain_ratio(X, Y, feat, val)
                if IGR > best_IGR:
                    best_IGR = IGR
                    best_feat = feat
                    best_val = val

        # 计算用best_feat <= best_val分类带来的代价函数变化.
        # 由于分裂叶结点只涉及该局部，我们只需要计算分裂前后该结点的代价函数
        # 当前代价
        cur_cost = len(Y) * self.entropy(Y) + self.lbd
        # 分裂后的代价，按best_feat的取值分类统计
        # 如果best_feat为None，说明最优的信息增益率为0，
        # 再分类也无法增加信息了，因此将new_cost设置为无穷大
        if best_feat is None:
            new_cost = np.inf
        else:
            new_cost = 0
            X_feat = X[:, best_feat]
            # 获取划分后的两部分，计算新的熵
            new_Y_l = Y[X_feat <= best_val]
            new_cost += len(new_Y_l) * self.entropy(new_Y_l)
            new_Y_r = Y[X_feat > best_val]
            new_cost += len(new_Y_r) * self.entropy(new_Y_r)
            # 分裂后会有两个叶结点
            new_cost += 2 * self.lbd

        if new_cost <= cur_cost:
            # 如果分裂后代价更小，那么执行分裂
            node.feat = best_feat
            node.split = best_val
            l_child = Node()
            l_X = X[X[:, best_feat] <= best_val]
            l_Y = Y[X[:, best_feat] <= best_val]
            self.ID3(l_child, l_X, l_Y)
            r_child = Node()
            r_X = X[X[:, best_feat] > best_val]
            r_Y = Y[X[:, best_feat] > best_val]
            self.ID3(r_child, r_X, r_Y)
            node.child = [l_child, r_child]
        else:
            # 否则将当前结点上最多的类别作为该结点的类别
            vals, cnt = np.unique(Y, return_counts=True)
            node.feat = vals[np.argmax(cnt)]
            self.T += 1

    # 预测新样本的分类
    def predict(self, x):
        node = self.root
        # 从根结点开始向下寻找，到叶结点结束
        while node.split is not None:
            # 判断x应该处于哪个子结点
            if x[node.feat] <= node.split:
                node = node.child[0]
            else:
                node = node.child[1]
        # 到达叶结点，返回类别
        return node.feat

    # 计算在样本X，标签Y上的准确率
    def accuracy(self, X, Y):
        correct = 0
        for x, y in zip(X, Y):
            pred = self.predict(x)
            if pred == y:
                correct += 1
        return correct / len(Y)

    # 新增功能：计算特征重要性
    def feature_importance(self):
        """计算特征重要性，根据特征在树中被选为分割点的频率"""
        importance = np.zeros(len(feat_names))
        self._calc_importance(self.root, importance)
        # 归一化
        if np.sum(importance) > 0:
            importance = importance / np.sum(importance)
        return importance

    def _calc_importance(self, node, importance):
        """递归计算特征重要性"""
        if node.split is not None:
            # 只有非叶节点才有特征
            importance[node.feat] += 1
            for child in node.child:
                self._calc_importance(child, importance)

    # 新增功能：混淆矩阵计算
    def confusion_matrix(self, X, Y):
        """计算混淆矩阵"""
        y_pred = [self.predict(x) for x in X]
        # 假设二分类问题，0为负类，1为正类
        tp = sum(1 for y, pred in zip(Y, y_pred) if y == 1 and pred == 1)
        tn = sum(1 for y, pred in zip(Y, y_pred) if y == 0 and pred == 0)
        fp = sum(1 for y, pred in zip(Y, y_pred) if y == 0 and pred == 1)
        fn = sum(1 for y, pred in zip(Y, y_pred) if y == 1 and pred == 0)
        return tp, tn, fp, fn

    # 新增功能：计算精确率、召回率和F1分数
    def precision_recall_f1(self, X, Y):
        """计算精确率、召回率和F1分数"""
        tp, tn, fp, fn = self.confusion_matrix(X, Y)
        precision = tp / (tp + fp) if (tp + fp) > 0 else 0
        recall = tp / (tp + fn) if (tp + fn) > 0 else 0
        f1 = 2 * precision * recall / (precision + recall) if (precision + recall) > 0 else 0
        return precision, recall, f1

    # 新增功能：预测样本属于各个类别的概率
    def predict_proba(self, x):
        """预测样本属于各个类别的概率"""
        node = self.root
        # 从根节点开始向下寻找，到叶节点结束
        while node.split is not None:
            # 判断x应该处于哪个子节点
            if x[node.feat] <= node.split:
                node = node.child[0]
            else:
                node = node.child[1]

        # 到达叶节点，返回概率（简单实现，实际上可以基于叶节点中的类别分布）
        return [1 - node.feat, node.feat]  # 假设二分类，返回[负类概率，正类概率]

    # 新增功能：计算ROC曲线和AUC值
    def roc_curve(self, X, Y):
        """计算ROC曲线和AUC值"""
        from sklearn.metrics import roc_curve, auc

        # 获取预测的正类概率
        y_proba = [self.predict_proba(x)[1] for x in X]

        # 计算FPR, TPR和阈值
        fpr, tpr, thresholds = roc_curve(Y, y_proba)

        # 计算AUC
        roc_auc = auc(fpr, tpr)

        return fpr, tpr, thresholds, roc_auc

    # 新增功能：保存模型到文件
    def save_model(self, filename):
        """保存模型到文件"""
        import pickle
        with open(filename, 'wb') as f:
            pickle.dump(self, f)
        print(f"模型已保存到 {filename}")

    # 新增功能：从文件加载模型
    @classmethod
    def load_model(cls, filename):
        """从文件加载模型"""
        import pickle
        with open(filename, 'rb') as f:
            model = pickle.load(f)
        print(f"模型已从 {filename} 加载")
        return model

    # 新增功能：可视化自定义决策树
    def visualize_tree(self, feature_names, max_depth=None):
        """可视化自定义的决策树"""

        def _add_node(node, parent, node_id, edge, ax, x, y, dx, depth=0):
            if max_depth is not None and depth > max_depth:
                return

            # 节点颜色
            if node.split is None:
                color = 'lightblue' if node.feat == 0 else 'lightcoral'
                label = f'类别: {node.feat}'
            else:
                color = 'lightgreen'
                feature = feature_names[node.feat]
                label = f'{feature} <= {node.split:.2f}'

            # 绘制节点
            circle = plt.Circle((x, y), 0.5, color=color, fill=True)
            ax.add_patch(circle)
            plt.text(x, y, label, ha='center', va='center', fontsize=8)

            # 连接父节点与当前节点
            if parent is not None:
                ax.plot([parent[0], x], [parent[1], y], 'k-')
                # 在边上添加标签
                plt.text((parent[0] + x) / 2, (parent[1] + y) / 2, edge,
                         ha='center', va='bottom', fontsize=8)

            # 递归绘制子节点
            if node.split is not None:
                dx = dx * 0.6  # 缩小水平间距
                _add_node(node.child[0], (x, y), node_id * 2, '是', ax, x - dx, y - 1.5, dx, depth + 1)
                _add_node(node.child[1], (x, y), node_id * 2 + 1, '否', ax, x + dx, y - 1.5, dx, depth + 1)

        # 创建绘图
        fig, ax = plt.subplots(figsize=(12, 8))
        ax.set_xlim(-10, 10)
        ax.set_ylim(-10, 2)
        ax.axis('off')

        # 从根节点开始绘制
        _add_node(self.root, None, 1, '', ax, 0, 0, 5)
        plt.title('自定义C4.5决策树可视化')
        plt.tight_layout()
        plt.savefig('custom_tree.png', dpi=300)
        plt.show()


# 新增功能：交叉验证
def cross_validation(X, Y, feat_ranges, k=5, lbd=1.0):
    """执行k折交叉验证"""
    from sklearn.model_selection import KFold

    kf = KFold(n_splits=k, shuffle=True, random_state=42)
    accuracies = []
    precisions = []
    recalls = []
    f1s = []

    for train_index, test_index in kf.split(X):
        X_train, X_test = X[train_index], X[test_index]
        Y_train, Y_test = Y[train_index], Y[test_index]

        # 训练模型
        model = DecisionTree(X_train, Y_train, feat_ranges, lbd)

        # 计算准确率
        acc = model.accuracy(X_test, Y_test)
        accuracies.append(acc)

        # 计算精确率、召回率和F1分数
        precision, recall, f1 = model.precision_recall_f1(X_test, Y_test)
        precisions.append(precision)
        recalls.append(recall)
        f1s.append(f1)

    print(f"{k}折交叉验证结果:")
    print(f"平均准确率: {np.mean(accuracies):.4f} ± {np.std(accuracies):.4f}")
    print(f"平均精确率: {np.mean(precisions):.4f} ± {np.std(precisions):.4f}")
    print(f"平均召回率: {np.mean(recalls):.4f} ± {np.std(recalls):.4f}")
    print(f"平均F1分数: {np.mean(f1s):.4f} ± {np.std(f1s):.4f}")

    return np.mean(accuracies)


# 新增功能：学习曲线
def plot_learning_curve(X, Y, feat_ranges, test_size=0.2, max_samples=None, step=50):
    """绘制学习曲线，展示训练样本数量与模型性能的关系"""
    from sklearn.model_selection import train_test_split

    X_train, X_test, Y_train, Y_test = train_test_split(
        X, Y, test_size=test_size, random_state=42)

    if max_samples is None:
        max_samples = len(X_train)

    train_sizes = np.arange(step, max_samples + 1, step)
    train_scores = []
    test_scores = []

    for size in train_sizes:
        idx = np.random.choice(len(X_train), min(size, len(X_train)), replace=False)
        X_subset = X_train[idx]
        Y_subset = Y_train[idx]

        model = DecisionTree(X_subset, Y_subset, feat_ranges, lbd=1.0)

        train_acc = model.accuracy(X_subset, Y_subset)
        test_acc = model.accuracy(X_test, Y_test)

        train_scores.append(train_acc)
        test_scores.append(test_acc)

        print(f"样本数: {size}, 训练准确率: {train_acc:.4f}, 测试准确率: {test_acc:.4f}")

    plt.figure(figsize=(10, 6))
    plt.plot(train_sizes, train_scores, 'o-', color='r', label='训练集准确率')
    plt.plot(train_sizes, test_scores, 'o-', color='g', label='测试集准确率')
    plt.xlabel('训练样本数')
    plt.ylabel('准确率')
    plt.title('学习曲线')
    plt.legend(loc='best')
    plt.grid(True)
    plt.savefig('learning_curve.png', dpi=300)
    plt.show()


# 训练自定义的决策树模型
print("训练自定义的C4.5决策树...")
DT = DecisionTree(train_x, train_y, feat_ranges, lbd=1.0)
print('叶结点数量：', DT.T)

# 计算在训练集和测试集上的准确率
print('训练集准确率：', DT.accuracy(train_x, train_y))
print('测试集准确率：', DT.accuracy(test_x, test_y))

# 使用sklearn的决策树进行比较
print('sklearn中的决策树')
from sklearn import tree

# criterion表示分类依据，max_depth表示树的最大深度
# entropy生成的是C4.5分类树
c45 = tree.DecisionTreeClassifier(criterion='entropy', max_depth=6)
c45.fit(train_x, train_y)
# gini生成的是CART分类树
cart = tree.DecisionTreeClassifier(criterion='gini', max_depth=6)
cart.fit(train_x, train_y)

c45_train_pred = c45.predict(train_x)
c45_test_pred = c45.predict(test_x)
cart_train_pred = cart.predict(train_x)
cart_test_pred = cart.predict(test_x)
print(f'训练集准确率：C4.5：{np.mean(c45_train_pred == train_y)}, ' \
      f'CART：{np.mean(cart_train_pred == train_y)}')
print(f'测试集准确率：C4.5：{np.mean(c45_test_pred == test_y)}，' \
      f'CART：{np.mean(cart_test_pred == test_y)}')

# 设置matplotlib使用中文字体
import matplotlib.font_manager as fm
import matplotlib as mpl

# 尝试设置中文字体
try:
    # Windows系统可以尝试使用以下字体
    font_path = 'C:/Windows/Fonts/SimSun.ttf'  # 宋体
    font_prop = fm.FontProperties(fname=font_path)
    plt.rcParams['font.family'] = font_prop.get_name()
    plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号
except:
    # 如果找不到指定字体，使用通用设置
    plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'SimSun', 'KaiTi', 'FangSong']
    plt.rcParams['axes.unicode_minus'] = False

# 使用matplotlib可视化sklearn的决策树
print("可视化sklearn的决策树...")
plt.figure(figsize=(15, 10))
tree.plot_tree(
    c45,
    feature_names=feat_names,
    class_names=['non-survival', 'survival'],
    filled=True,
    rounded=True
)
plt.title('sklearn C4.5决策树可视化')
plt.tight_layout()
plt.savefig('sklearn_c45_tree.png', dpi=300)
plt.show()

plt.figure(figsize=(15, 10))
tree.plot_tree(
    cart,
    feature_names=feat_names,
    class_names=['non-survival', 'survival'],
    filled=True,
    rounded=True
)
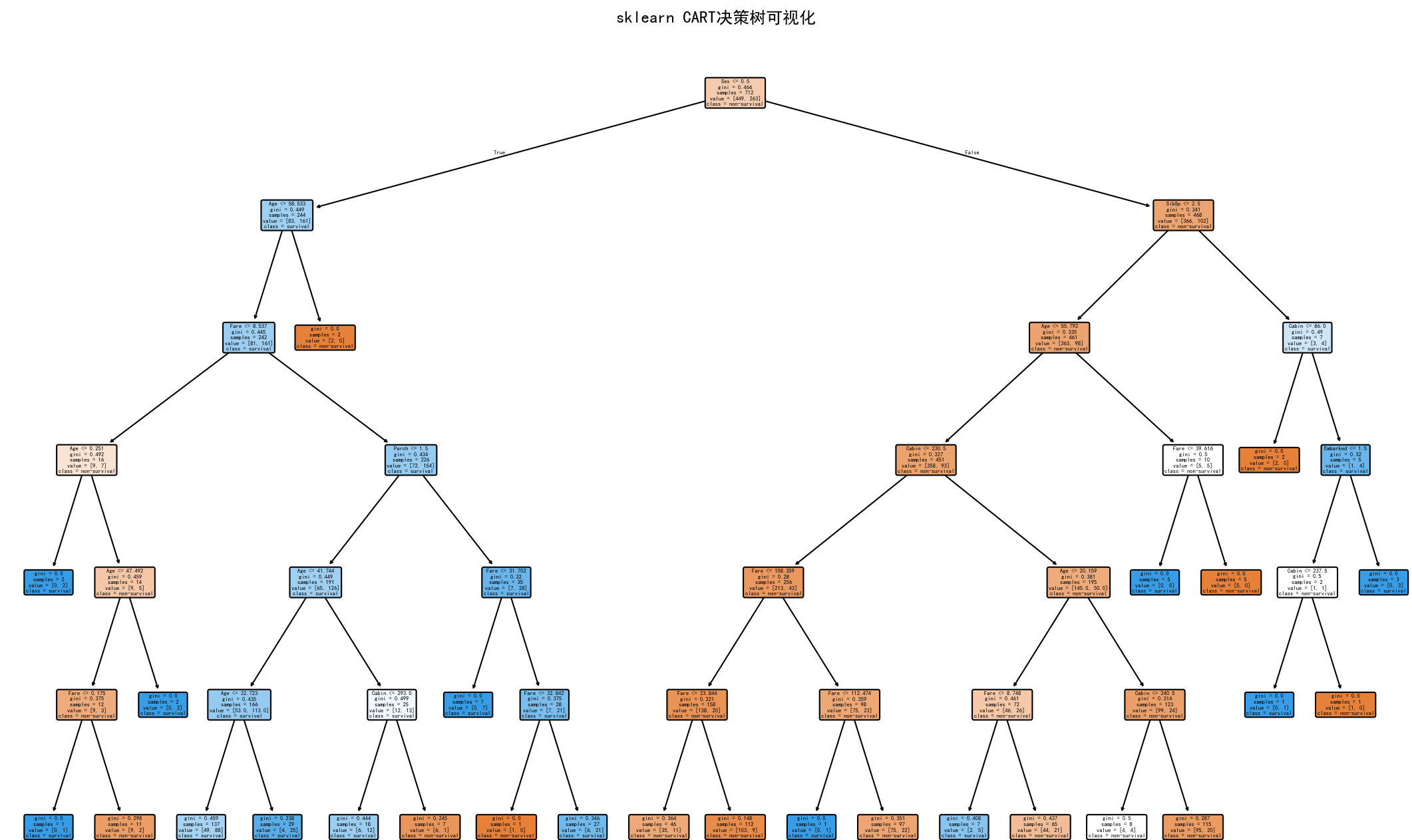
plt.title('sklearn CART决策树可视化')
plt.tight_layout()
plt.savefig('sklearn_cart_tree.png', dpi=300)
plt.show()

# 使用新增功能

# 1. 计算并展示特征重要性
print("计算特征重要性...")
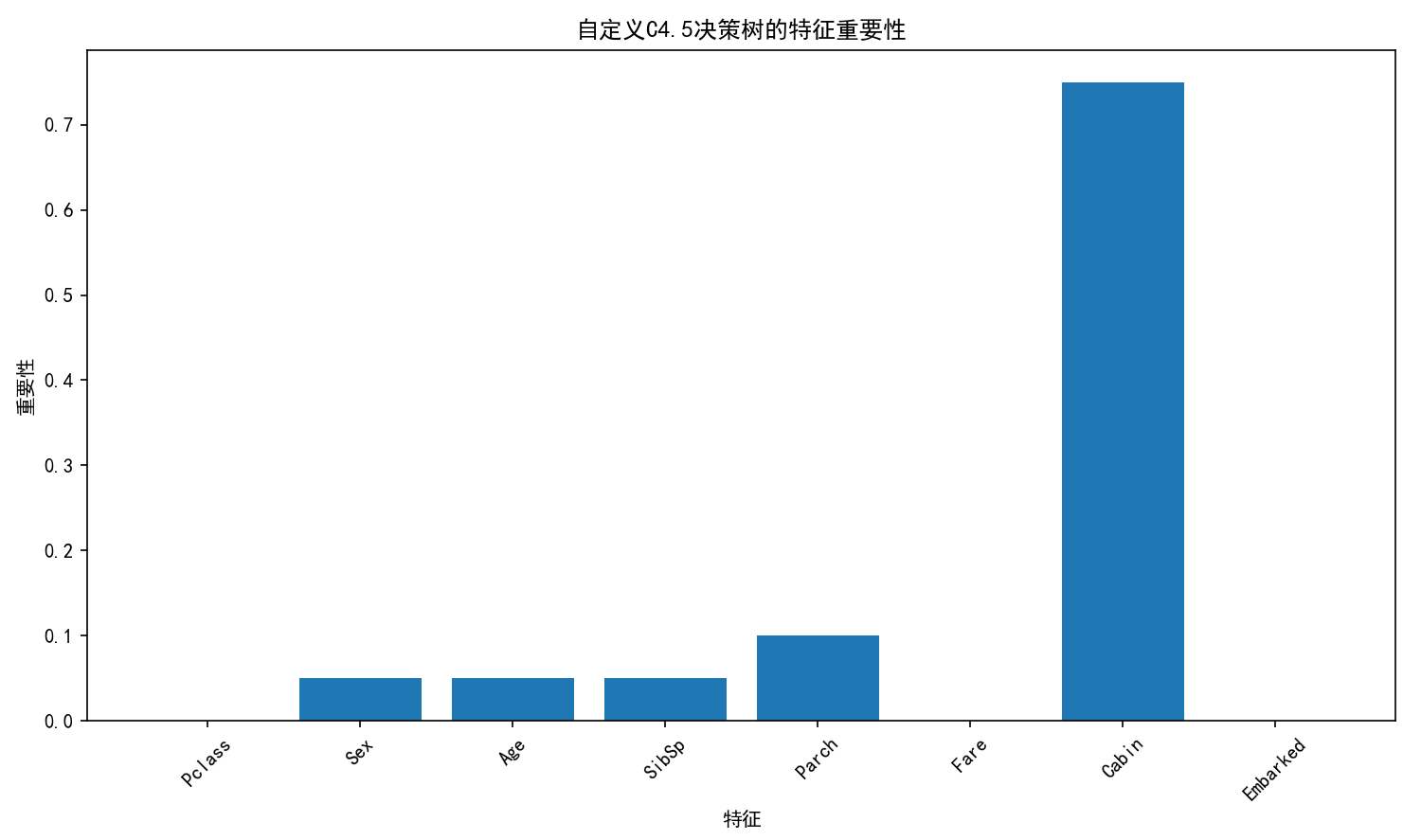
importance = DT.feature_importance()

plt.figure(figsize=(10, 6))
plt.bar(feat_names, importance)
plt.xticks(rotation=45)
plt.xlabel('特征')
plt.ylabel('重要性')
plt.title('自定义C4.5决策树的特征重要性')
plt.tight_layout()
plt.savefig('feature_importance.png', dpi=300)
plt.show()

# 2. 显示混淆矩阵和评估指标
print("计算混淆矩阵和评估指标...")
tp, tn, fp, fn = DT.confusion_matrix(test_x, test_y)
precision, recall, f1 = DT.precision_recall_f1(test_x, test_y)

print("混淆矩阵:")
print(f"真正例(TP): {tp}")
print(f"真负例(TN): {tn}")
print(f"假正例(FP): {fp}")
print(f"假负例(FN): {fn}")
print(f"精确率: {precision:.4f}")
print(f"召回率: {recall:.4f}")
print(f"F1分数: {f1:.4f}")

# 3. 绘制ROC曲线
print("绘制ROC曲线...")
fpr, tpr, _, roc_auc = DT.roc_curve(test_x, test_y)

plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正例率')
plt.ylabel('真正例率')
plt.title('ROC曲线')
plt.legend(loc="lower right")
plt.savefig('roc_curve.png', dpi=300)
plt.show()

# 4. 保存和加载模型
print("保存和加载模型...")
DT.save_model('decision_tree_model.pkl')
loaded_DT = DecisionTree.load_model('decision_tree_model.pkl')
print(f"加载后的模型准确率: {loaded_DT.accuracy(test_x, test_y):.4f}")

# 5. 执行交叉验证
print("执行五折交叉验证...")
cv_accuracy = cross_validation(train_x, train_y, feat_ranges, k=5, lbd=1.0)

# 6. 可视化自定义决策树
print("可视化自定义决策树...")
DT.visualize_tree(feat_names, max_depth=3)

# 7. 绘制学习曲线
print("绘制学习曲线...")
plot_learning_curve(train_x, train_y, feat_ranges, test_size=0.2, max_samples=500, step=50)

程序运行结果如下：

由于随机生成的数据量很大，这里只给出部分截图

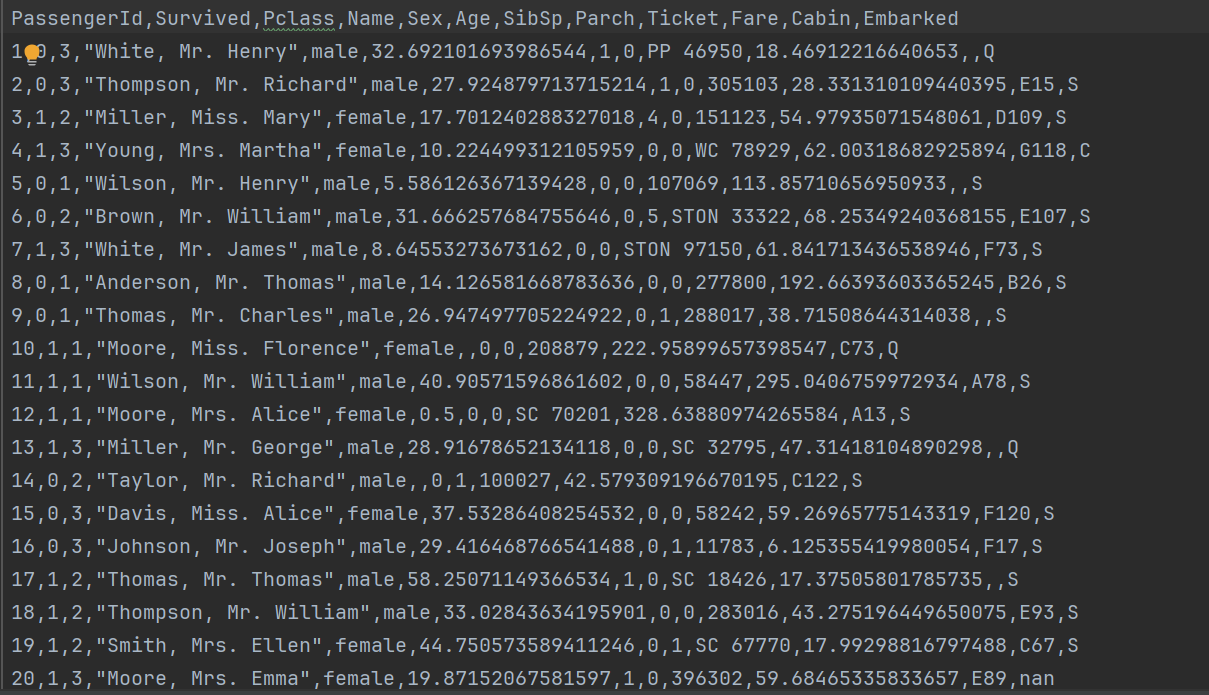
动手实现C4.5算法的决策树
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 891 non-null int64
1 Survived 891 non-null int64
2 Pclass 891 non-null int64
3 Name 891 non-null object
4 Sex 891 non-null object
5 Age 713 non-null float64
6 SibSp 891 non-null int64
7 Parch 891 non-null int64
8 Ticket 891 non-null object
9 Fare 891 non-null float64
10 Cabin 679 non-null object
11 Embarked 879 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.7+ KB
None
PassengerId Survived Pclass ... Fare Cabin Embarked
0 1 0 3 ... 18.469122 NaN Q
1 2 0 3 ... 28.331310 E15 S
2 3 1 2 ... 54.979351 D109 S
3 4 1 3 ... 62.003187 G118 C
4 5 0 1 ... 113.857107 NaN S

[5 rows x 12 columns]
Age :
0.5000
8.5408
16.5816
24.6224
32.6632
40.7040
48.7448
56.7856
64.8265
72.8673
Fare :
0.0166
56.7349
113.4532
170.1715
226.8898
283.6081
340.3264
397.0447
453.7631
510.4814
Sex: Index(['female', 'male'], dtype='object')
Pclass: Index([1, 2, 3], dtype='int64')
SibSp: Index([0, 1, 2, 3, 4, 5], dtype='int64')
Parch: Index([0, 1, 2, 3, 4, 5], dtype='int64')
Cabin: Index(['A103', 'A107', 'A109', 'A110', 'A112', 'A12', 'A125', 'A129', 'A13',
'A130',
...
'G80', 'G81', 'G83', 'G85', 'G86', 'G87', 'G92', 'G93', 'G97', 'G99'],
dtype='object', length=481)
Embarked: Index(['C', 'Q', 'S'], dtype='object')
训练集大小： 712
测试集大小： 179
特征数： 8
训练自定义的C4.5决策树...
叶结点数量： 21
训练集准确率： 0.7682584269662921
测试集准确率： 0.7318435754189944
sklearn中的决策树
训练集准确率：C4.5：0.7752808988764045, CART：0.7794943820224719
测试集准确率：C4.5：0.7039106145251397，CART：0.7374301675977654
可视化sklearn的决策树...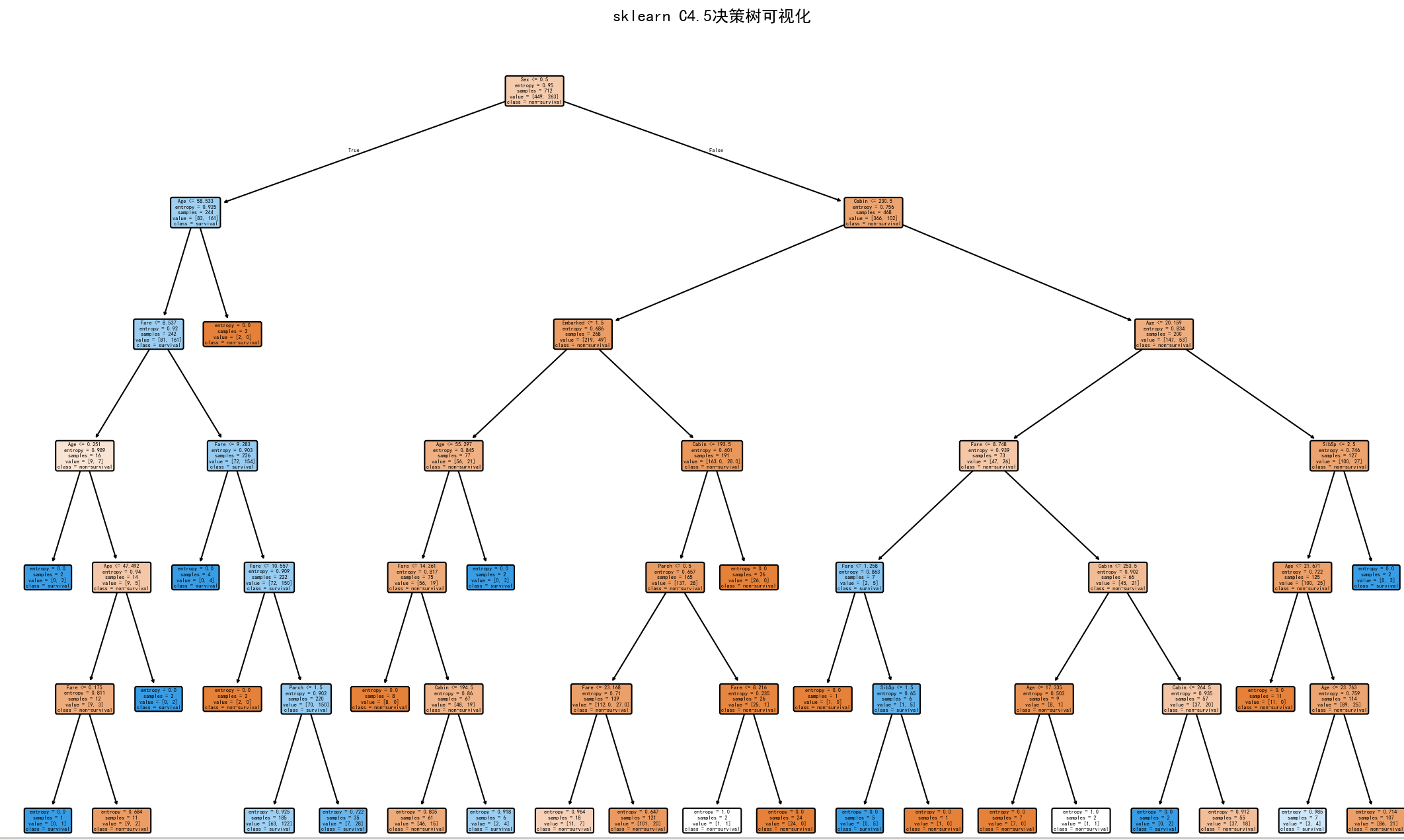

计算特征重要性...

计算混淆矩阵和评估指标...
混淆矩阵:
真正例(TP): 43
真负例(TN): 88
假正例(FP): 24
假负例(FN): 24
精确率: 0.6418
召回率: 0.6418
F1分数: 0.6418
绘制ROC曲线...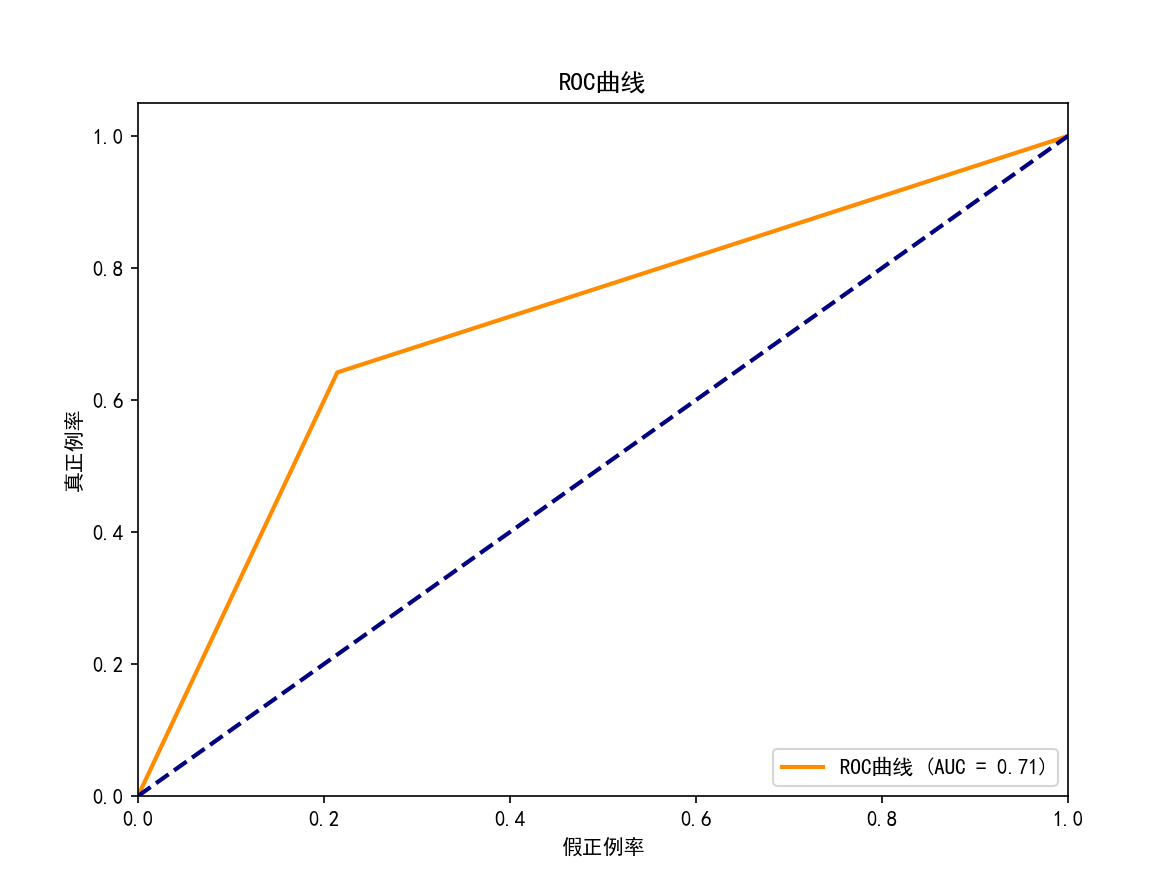

保存和加载模型...
模型已保存到 decision_tree_model.pkl
模型已从 decision_tree_model.pkl 加载
加载后的模型准确率: 0.7318
执行五折交叉验证...
5折交叉验证结果:
平均准确率: 0.7219 ± 0.0322
平均精确率: 0.6374 ± 0.0308
平均召回率: 0.5795 ± 0.0357
平均F1分数: 0.6062 ± 0.0247
可视化自定义决策树...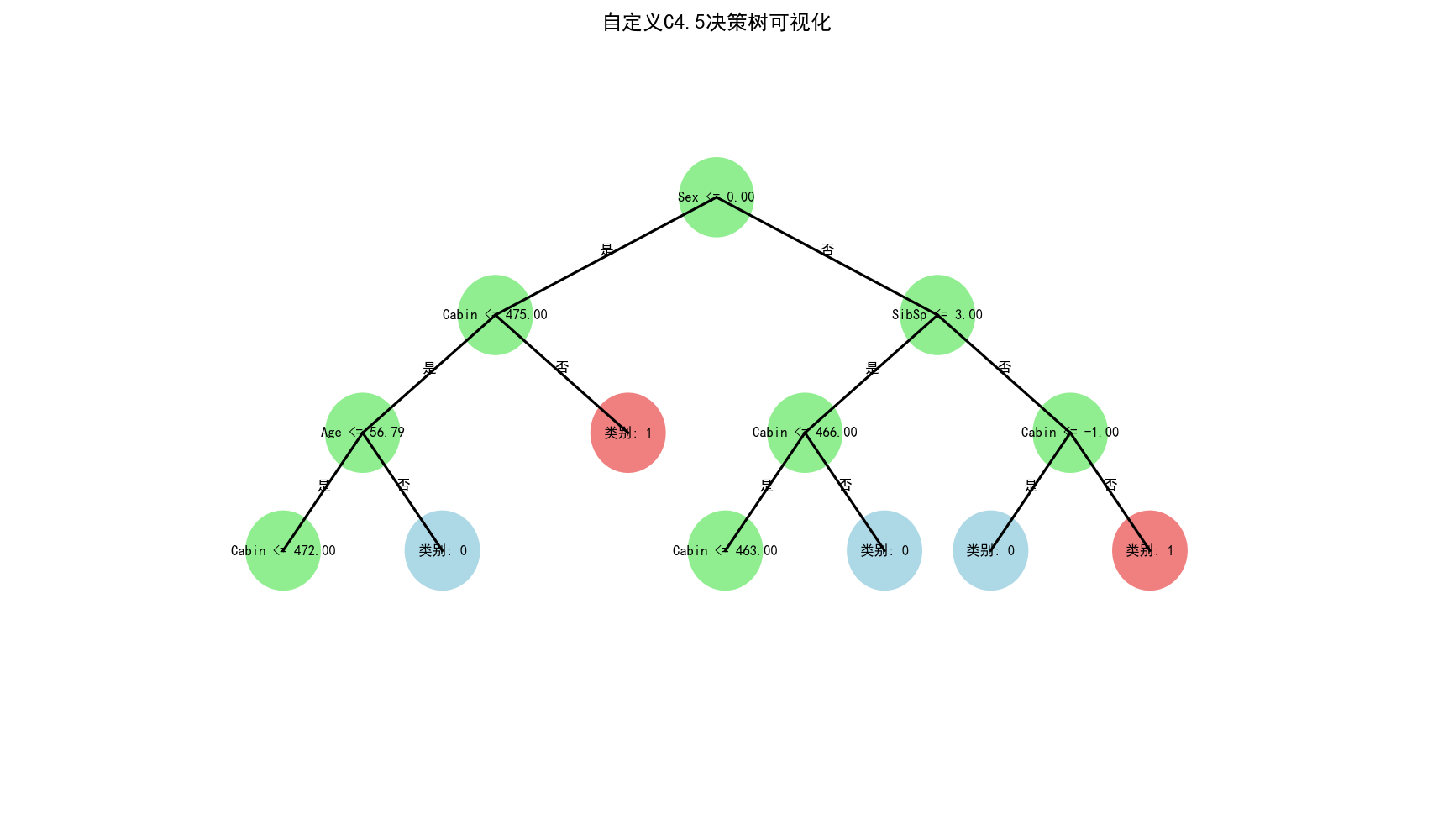

绘制学习曲线...
样本数: 50, 训练准确率: 0.9600, 测试准确率: 0.6294
样本数: 100, 训练准确率: 0.9100, 测试准确率: 0.7063
样本数: 150, 训练准确率: 0.8933, 测试准确率: 0.6364
样本数: 200, 训练准确率: 0.7950, 测试准确率: 0.7343
样本数: 250, 训练准确率: 0.7680, 测试准确率: 0.7133
样本数: 300, 训练准确率: 0.8433, 测试准确率: 0.6853
样本数: 350, 训练准确率: 0.7171, 测试准确率: 0.7413
样本数: 400, 训练准确率: 0.7750, 测试准确率: 0.7203
样本数: 450, 训练准确率: 0.7778, 测试准确率: 0.7203
样本数: 500, 训练准确率: 0.7840, 测试准确率: 0.7273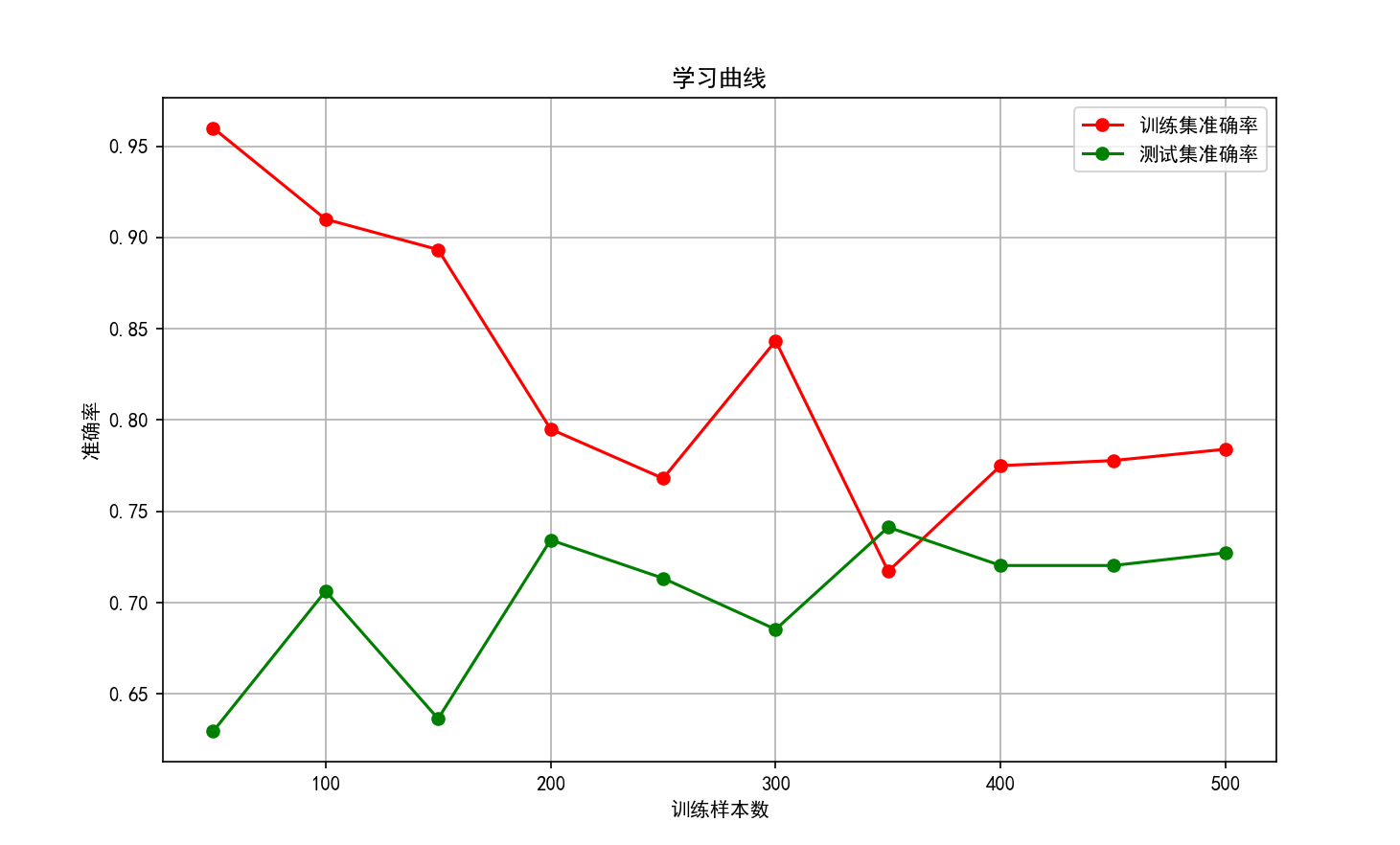

最后程序生成的目录如下：

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐