机器学习算法——概率图模型（隐马尔可夫模型1）

HMM的三大要素和三大假设

Vicky_xiduoduo

973人浏览 · 2022-10-11 11:17:57

Vicky_xiduoduo · 2022-10-11 11:17:57 发布

概率图模型是一类用图来表达变量相关关系的概率模型。

概率图模型可分为两类：第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网；第二类是使用无向图表示变量间的相关关系，称为无向图模型或马尔可夫网。

隐马尔可夫模型（Hidden Markov Model,HMM）是结构最简单的动态贝叶斯网，这是一种著名的有向图模型。

一个马尔可夫过程是状态间的转移仅依赖于前n个状态的过程，这个过程称之为n阶马尔可夫模型。

最简单的马尔可夫过程是一阶模型，它的状态选择只依赖于前一个状态。

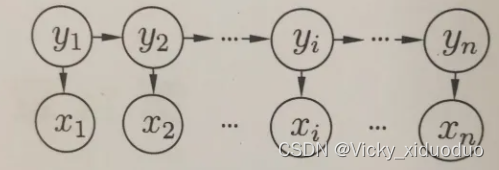
图1 隐马尔可夫模型的图结构

$x_i \in X$ 隐马尔可夫模型中的变量可分为两组，第一组是状态变量 $\{y_1,y_2,...,y_n\}$ ，其中 $y_i \in Y$ 表示第i时刻的系统状态，这个状态变量一般是隐藏的，不被观测的，因此状态变量亦称为隐变量；第二组是观测变量 $\{x_1,x_2,...,x_n\}$ ，其中 $x_i \in X$ 表示第i个时刻的观测值。

在隐马尔可夫模型中，系统通常在多个状态 $\{s_1,s_2,...,s_N\}$ 之间转换；观测变量的取值范围为 $\{o_1,o_2,...,o_M\}$ 。注意，隐藏状态与观测状态的数目不一定相同。

图1中的箭头表示变量间的依赖关系，在任一时刻，观测变量的取值仅依赖于状态变量，即 $x_t$ 由 $y_t$ 决定。同时，t时刻的状态 $y_t$ 仅依赖于t-1时刻的状态 $y_{t-1}$ ,与其余n-2个状态无关，这就是所谓的“马尔可夫链”，即：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态。

基于这种依赖关系，所有变量的联合概率分布为：

$P(x_1,y_1,...,x_n,y_n)=P(y_1)P(x_1|y_1) \prod_{i=2}^{n}P(y_i|y_{i-1})P(x_i|y_i)$

欲确定一个隐马尔可夫模型还需要以下三大要素：

1.状态转移概率：模型在各个状态间转移的概率，通常记为矩阵 $A=[a_{ij}]_{N \times N}$ ,其中

$a_{ij} = P(y_{t+1}=s_j|y_t=s_i)$

表示在任意时刻t，若状态为 $s_i$ ,则在下一时刻状态为 $s_j$ 的概率。

2.输出观测概率：模型根据当前状态获得各个观测值的概率，通常记为矩阵 $B=[b_{ij}]_{N\times M}$ ,其中

$b_i(j)=P(x_t=o_j|y_t=s_i)$

表示在任意时刻t，若状态为 $s_i$ ，则观测值 $o_j$ 被获取的概率。

3.初始状态概率：模型在初始时刻各状态出现的概率，通常记为 $\pi=(\pi_1,\pi_2,...\pi_N)$ ，其中

$\pi_i = P(y_1=s_i)$

表示模型的初始状态为 $s_i$ 的概率。

隐马尔可夫模型还有三个假设：

（1）齐次马尔可夫假设（一阶马尔可夫假设）：任意时刻的状态只依赖于前一时刻的状态，与其他时刻无关，符号表示为：

$P(y_t|y_{t-1},x_{t-1},...,y_1,x_1)=P(y_t|y_{t-1})$

（2）观测独立假设：任意时刻的观测只依赖于该时刻的状态，与其他状态无关，符号表示为：

$P(x_t|y_T,x_T,....y_t,x_t,.....y_1,x_1)=P(x_t|y_t)$

（3）参数不变性假设：上面介绍的三大要素不随时间的变化而改变，即整个训练过程中一直保持不变。

HMM介绍了三大要素和三大假设，能够解决以下三大问题：概率计算问题、预测问题和学习问题。这些后面章节再继续介绍。

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐