论文复现 | 登神长阶:时序预测模型系列推送9——CNN-LSTM-Attention
CNN-LSTM-Attention模型通过整合卷积神经网络(CNN)、长短期记忆网络(LSTM)和注意力机制,实现了对复杂数据任务的高效处理。CNN负责提取空间特征,LSTM捕捉时间序列的长期依赖关系,而注意力机制则动态聚焦关键信息,提升模型处理精度。该模型在多维特征挖掘、泛化能力和多变量数据处理方面表现出色,广泛应用于经济预测、气象预报、金融市场分析和能源需求预测等领域。通过代码实现,模型能够
在深度学习技术不断演进的当下,CNN-LSTM-Attention 模型凭借其独特的架构设计,成为处理复杂数据任务的利器。该模型通过创新性地整合卷积神经网络(CNN)、长短期记忆网络(LSTM)与注意力机制,实现了对数据特征的深度挖掘与精准预测。
一、核心组件的协同运作机制
1. CNN:空间特征的自动提取器
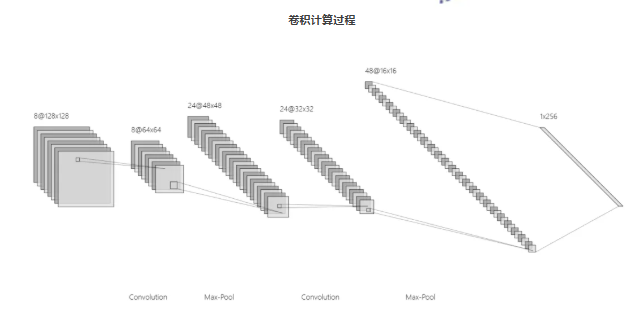
CNN 作为专为结构化数据设计的神经网络,其核心在于卷积操作的巧妙运用。通过预设的卷积核在数据矩阵上进行滑动扫描,CNN 能够高效捕捉数据中的局部模式。这一过程如同使用不同规格的滤镜,从原始数据中筛选出边缘、纹理等基础特征。随着卷积层的叠加,模型可逐步提炼出从基础到高级的语义特征,完成对数据空间结构的深度解析。
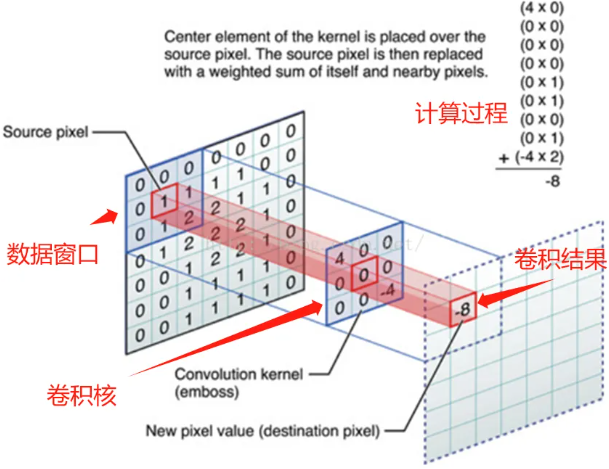
2. LSTM:时间序列的记忆大师
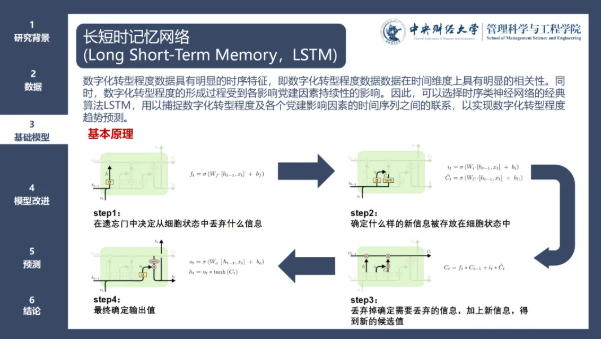
作为 RNN 的进阶版本,LSTM 着力解决传统 RNN 在处理长序列时面临的梯度问题。其核心的门控机制由输入门、遗忘门和输出门构成。输入门决定新信息的接纳程度,遗忘门调控历史信息的保留比例,输出门则筛选出用于当前决策的关键信息。这种精密的门控系统,使 LSTM 能够在长序列数据中精准捕捉时间依赖关系,避免重要信息的流失。
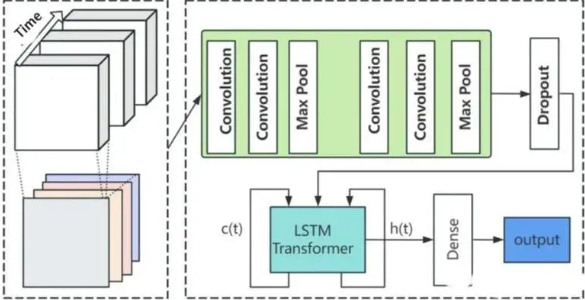
CNN-LSTM 结合原理:CNN-LSTM 算法将 CNN 对空间特征的提取能力和 LSTM 对时间特征的捕捉能力相结合。首先,使用 CNN 对输入的时间序列数据进行特征提取,得到具有代表性的特征图。然后,将这些特征图作为 LSTM 的输入,利用 LSTM 对时间序列的长期依赖关系进行建模和预测。
3. 注意力机制:动态聚焦的智能选择器
注意力机制赋予模型动态分配权重的能力,其通过计算输入序列各部分与当前任务的关联度,生成对应的注意力权重。这使得模型能够在海量信息中自动聚焦关键部分,显著提升信息处理的效率与针对性。在序列处理任务中,该机制尤其擅长捕捉关键节点,有效提升模型的处理精度。
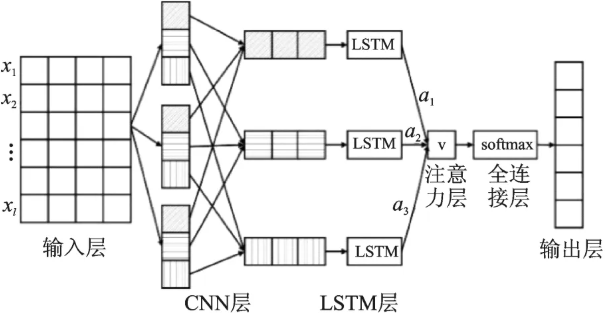
4. 三位一体的融合逻辑
CNN-LSTM-Attention 模型将三者优势有机整合:首先利用 CNN 对时间序列数据进行特征提取,生成浓缩的特征图谱;继而将这些特征图谱输入 LSTM,完成时间维度的信息建模;最后,注意力机制对 LSTM 输出进行优化,使模型能够根据任务需求动态调整关注重点,实现更精准的预测与分析。
二、架构融合的显著优势
1. 多维特征的深度挖掘
该模型实现了特征提取的多维度突破:CNN 负责捕捉数据的局部特征,LSTM 解析时间序列的长期依赖,注意力机制则进一步增强关键特征的识别能力。三者协同工作,能够从复杂时间序列数据中提炼出更全面、深入的特征信息。
2. 卓越的泛化与适应能力
得益于 CNN 的局部特征提取、LSTM 的记忆功能和注意力机制的动态选择,模型在面对不同类型任务与数据时展现出良好的适应性,有效提升了预测性能与泛化能力。
3. 多变量数据的高效处理
模型支持多变量输入,能够同时处理多个相互关联的特征维度,精准捕捉数据间的复杂关系,特别适用于多源异构数据的分析场景。
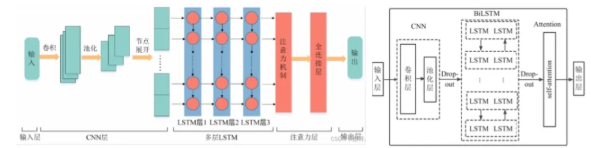
三、广泛的实际应用场景
1. 经济领域的智能预测
在经济数据分析中,该模型可通过分析历史经济数据,对通货膨胀率、失业率、GDP 增长等关键指标进行精准预测,为政策制定与企业决策提供科学依据。
2. 气象领域的精准预报
在气象预测方面,模型通过整合气温、气压、风速等多维气象数据,显著提升天气预报的准确性,为灾害预警与资源调度提供可靠支持。
3. 金融市场的趋势研判
在股票市场分析中,模型通过解析股价、成交量、财务数据等信息,捕捉市场波动规律,辅助投资者制定科学的投资策略,有效降低投资风险。
4. 能源领域的需求预测
在能源管理领域,模型可对电力、石油、天然气等能源消耗数据进行分析,精准预测能源需求,助力优化能源分配,提升能源利用效率。
CNN-LSTM-Attention 模型凭借其创新的架构设计与强大的处理能力,为时间序列分析与预测提供了高效解决方案,在众多领域展现出巨大的应用潜力,将持续推动相关领域的智能化发展进程。
代码
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
tic
% restoredefaultpath
%% 导入数据
res = xlsread('自己的excel数据');
%% 数据分析
num_size = 0.7; % 训练集占数据集比例
outdim = 1; % 最后一列为输出
num_samples = size(res, 1); % 样本个数
res = res(randperm(num_samples), :); % 打乱数据集(不希望打乱时,注释该行)
num_train_s = ceil(num_size * num_samples)+1; % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度
%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 数据平铺
% 将数据平铺成1维数据只是一种处理方式
% 也可以平铺成2维数据,以及3维数据,需要修改对应模型结构
% 但是应该始终和输入层数据结构保持一致
p_train = double(reshape(p_train, f_, 1, 1, M));
p_test = double(reshape(p_test , f_, 1, 1, N));
t_train = double(t_train)';
t_test = double(t_test )';
%% 数据格式转换
for i = 1 : M
Lp_train{i, 1} = p_train(:, :, 1, i);
end
for i = 1 : N
Lp_test{i, 1} = p_test( :, :, 1, i);
end
%% 建立模型
lgraph = layerGraph(); % 建立空白网络结构
tempLayers = [
sequenceInputLayer([f_, 1, 1], "Name", "sequence") % 建立输入层,输入数据结构为[f_, 1, 1]
sequenceFoldingLayer("Name", "seqfold")]; % 建立序列折叠层
lgraph = addLayers(lgraph, tempLayers); % 将上述网络结构加入空白结构中
tempLayers = convolution2dLayer([1, 1], 32, "Name", "conv_1"); % 卷积层 卷积核[1, 1] 步长[1, 1] 通道数 32
lgraph = addLayers(lgraph,tempLayers); % 将上述网络结构加入空白结构中
tempLayers = [
reluLayer("Name", "relu_1") % 激活层
convolution2dLayer([1, 1], 64, "Name", "conv_2") % 卷积层 卷积核[1, 1] 步长[1, 1] 通道数 64
reluLayer("Name", "relu_2")]; % 激活层
lgraph = addLayers(lgraph, tempLayers); % 将上述网络结构加入空白结构中
tempLayers = [
globalAveragePooling2dLayer("Name", "gapool") % 全局平均池化层
fullyConnectedLayer(16, "Name", "fc_2") % SE注意力机制,通道数的1 / 4
reluLayer("Name", "relu_3") % 激活层
fullyConnectedLayer(64, "Name", "fc_3") % SE注意力机制,数目和通道数相同
sigmoidLayer("Name", "sigmoid")]; % 激活层
lgraph = addLayers(lgraph, tempLayers); % 将上述网络结构加入空白结构中
tempLayers = multiplicationLayer(2, "Name", "multiplication"); % 点乘的注意力
lgraph = addLayers(lgraph, tempLayers); % 将上述网络结构加入空白结构中
tempLayers = [
sequenceUnfoldingLayer("Name", "sequnfold") % 建立序列反折叠层
flattenLayer("Name", "flatten") % 网络铺平层
lstmLayer(6, "Name", "lstm", "OutputMode", "last") % lstm层
fullyConnectedLayer(1, "Name", "fc") % 全连接层
regressionLayer("Name", "regressionoutput")]; % 回归层
lgraph = addLayers(lgraph, tempLayers); % 将上述网络结构加入空白结构中
lgraph = connectLayers(lgraph, "seqfold/out", "conv_1"); % 折叠层输出 连接 卷积层输入;
lgraph = connectLayers(lgraph, "seqfold/miniBatchSize", "sequnfold/miniBatchSize");
% 折叠层输出 连接 反折叠层输入
lgraph = connectLayers(lgraph, "conv_1", "relu_1"); % 卷积层输出 链接 激活层
lgraph = connectLayers(lgraph, "conv_1", "gapool"); % 卷积层输出 链接 全局平均池化
lgraph = connectLayers(lgraph, "relu_2", "multiplication/in2"); % 激活层输出 链接 相乘层
lgraph = connectLayers(lgraph, "sigmoid", "multiplication/in1"); % 全连接输出 链接 相乘层
lgraph = connectLayers(lgraph, "multiplication", "sequnfold/in"); % 点乘输出
%% 参数设置
options = trainingOptions('adam', ... % Adam 梯度下降算法
'MaxEpochs', 200, ... % 最大迭代次数
'InitialLearnRate', 1e-2, ... % 初始学习率为0.01
'LearnRateSchedule', 'piecewise', ... % 学习率下降
'LearnRateDropFactor', 0.5, ... % 学习率下降因子 0.5
'LearnRateDropPeriod', 150, ... % 经过700次训练后 学习率为 0.01 * 0.1
'Shuffle', 'every-epoch', ... % 每次训练打乱数据集
'Plots', 'training-progress', ... % 画出曲线
'Verbose', false);
%% 训练模型
net = trainNetwork(Lp_train, t_train, lgraph, options);
%% 模型预测
t_sim1 = predict(net, Lp_train);
t_sim2 = predict(net, Lp_test );
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1', ps_output);
T_sim2 = mapminmax('reverse', t_sim2', ps_output);
T_sim1=double(T_sim1);
T_sim2=double(T_sim2);
%% 显示网络结构
% analyzeNetwork(net)
%% 测试集结果
figure;
plotregression(T_test,T_sim2,['回归图']);
figure;
ploterrhist(T_test-T_sim2,['误差直方图']);
%% 均方根误差 RMSE
error1 = sqrt(sum((T_sim1 - T_train).^2)./M);
error2 = sqrt(sum((T_test - T_sim2).^2)./N);
%%
%决定系数
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test ))^2;
%%
%均方误差 MSE
mse1 = sum((T_sim1 - T_train).^2)./M;
mse2 = sum((T_sim2 - T_test).^2)./N;
%%
%RPD 剩余预测残差
SE1=std(T_sim1-T_train);
RPD1=std(T_train)/SE1;
SE=std(T_sim2-T_test);
RPD2=std(T_test)/SE;
%% 平均绝对误差MAE
MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
% MAPE1 = mean(abs((T_train - T_sim1)./T_train));
% MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%% 训练集绘图
figure
plot(1:M,T_train,'r-*',1:M,T_sim1,'b-o','LineWidth',1)
plot(1:M,T_train,'r-',1:M,T_sim1,'b-','LineWidth',1.5)
legend('真实值','CNN-LSTM-Attention预测值')
xlabel('预测样本')
ylabel('预测结果')
string={'训练集预测结果对比';['(R^2 =' num2str(R1) ' RMSE= ' num2str(error1) ' MSE= ' num2str(mse1) ' RPD= ' num2str(RPD1) ')' ]};
title(string)
%% 预测集绘图
figure
plot(1:N,T_test,'r-',1:N,T_sim2,'b-','LineWidth',1.5)
legend('真实值','CNN-LSTM-Attention预测值')
xlabel('预测样本')
ylabel('预测结果')
string={'测试集预测结果对比';['(R^2 =' num2str(R2) ' RMSE= ' num2str(error2) ' MSE= ' num2str(mse2) ' RPD= ' num2str(RPD2) ')']};
title(string)
%% 测试集误差图
figure
ERROR3=T_test-T_sim2;
plot(T_test-T_sim2,'b-*','LineWidth',1.5)
xlabel('测试集样本编号')
ylabel('预测误差')
title('测试集预测误差')
grid on;
legend('预测输出误差')
%% 绘制线性拟合图
%% 训练集拟合效果图
figure
plot(T_train,T_sim1,'*r');
xlabel('真实值')
ylabel('预测值')
string = {'训练集效果图';['R^2_c=' num2str(R1) ' RMSEC=' num2str(error1) ]};
title(string)
hold on ;h=lsline;
set(h,'LineWidth',1,'LineStyle','-','Color',[1 0 1])
%% 预测集拟合效果图
figure
plot(T_test,T_sim2,'ob');
xlabel('真实值')
ylabel('预测值')
string1 = {'测试集效果图';['R^2_p=' num2str(R2) ' RMSEP=' num2str(error2) ]};
title(string1)
hold on ;h=lsline();
set(h,'LineWidth',1,'LineStyle','-','Color',[1 0 1])
%% 求平均
R3=(R1+R2)./2;
error3=(error1+error2)./2;
%% 总数据线性预测拟合图
tsim=[T_sim1,T_sim2]';
S=[T_train,T_test]';
figure
plot(S,tsim,'ob');
xlabel('真实值')
ylabel('预测值')
string1 = {'所有样本拟合预测图';['R^2_p=' num2str(R3) ' RMSEP=' num2str(error3) ]};
title(string1)
hold on ;h=lsline();
set(h,'LineWidth',1,'LineStyle','-','Color',[1 0 1])
%% 打印出评价指标
disp(['-----------------------误差计算--------------------------'])
disp(['评价结果如下所示:'])
disp(['平均绝对误差MAE为:',num2str(MAE2)])
disp(['均方误差MSE为: ',num2str(mse2)])
disp(['均方根误差RMSE为: ',num2str(error2)])
disp(['决定系数R^2为: ',num2str(R2)])
disp(['剩余预测残差RPD为: ',num2str(RPD2)])
%disp(['平均绝对百分比误差MAPE为: ',num2str(MAPE2)])
grid
%% 训练集和测试集的指标记录
ana=[R1,MAE1,error1,R2,MAE2,error2];
pre_result=[T_sim2',T_test'];计算结果
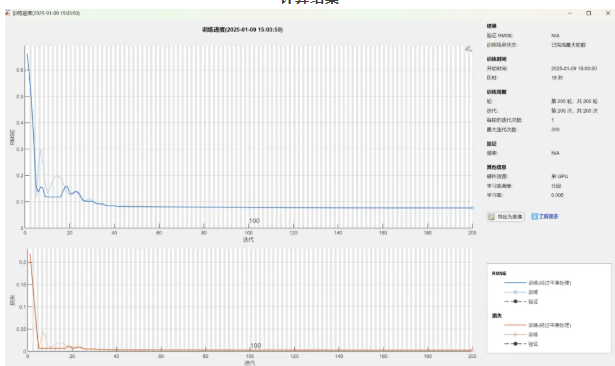
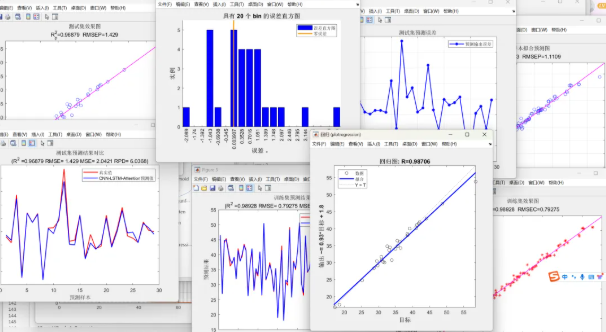
训练过程,可以看到误差逐渐收敛到较小值
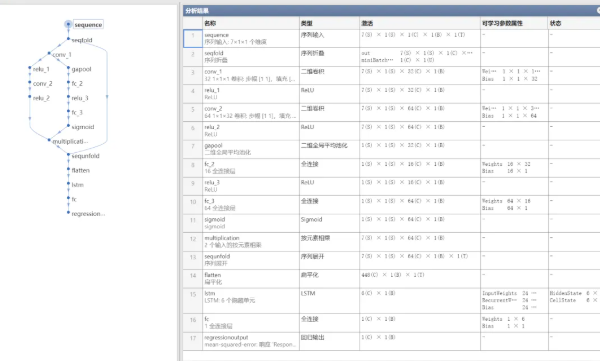
复杂的三重并行网络,但是CNN和attention占据的参数不多,最后的参数总量依然是十万级的。其他主要参数量还是LSTM贡献的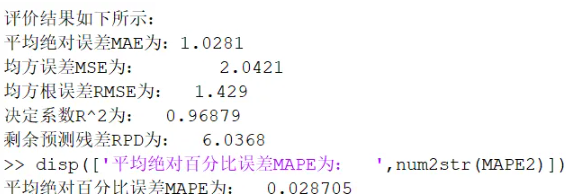
这些是我的学长做的,这玩意是可以预测期权、股票、债券等金融数据的,但是需要进一步的改进,进一步降低预测误差,希望把MAPE降低到1%以内。已经做了一些工作,敬请大家关注我之后的系列推送。这里也给大家准备了论文复现文档和更多创新点的资料,大家可以扫码找我领取哈~

GitCode 天启AI是一款由 GitCode 团队打造的智能助手,基于先进的LLM(大语言模型)与多智能体 Agent 技术构建,致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话,还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力,真正做到“一句话,让 Al帮你完成复杂任务”。
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容









所有评论(0)