带你从入门到精通——自然语言处理（四. GRU和seq2seq模型）

门控循环单元（GRU，Gated Recurrent Unit）与LSTM一样是一种改进版的RNN，GRU也通过引入门控机制来更好地捕捉长序列数据中的长期依赖关系。GRU的内部结构图如下：在GRU中门控机制中一共有两个门，下式中的σ表示sigmoid激活函数：重置门：该门决定了在计算候选隐藏状态时，上一个时间步的隐藏状态中哪些信息应该被重置（遗忘），它接收当前时间步的输入和上一个时间步的隐藏状态，

2401_86480334

1038人浏览 · 2025-03-05 17:37:16

2401_86480334 · 2025-03-05 17:37:16 发布

建议先阅读我之前的博客，掌握一定的自然语言处理前置知识后再阅读本文，链接如下：

带你从入门到精通——自然语言处理（一. 文本的基本预处理方法和张量表示）-CSDN博客

带你从入门到精通——自然语言处理（二. 文本数据分析、特征处理和数据增强）-CSDN博客

带你从入门到精通——自然语言处理（三. RNN的分类和LSTM）-CSDN博客

4.2.4 Teacher Forcing

四. GRU和seq2seq模型

4.1 GRU

4.1.1 GRU概述

门控循环单元（GRU，Gated Recurrent Unit）与LSTM一样是一种改进版的RNN，GRU也通过引入门控机制来更好地捕捉长序列数据中的长期依赖关系。

GRU的内部结构图如下：

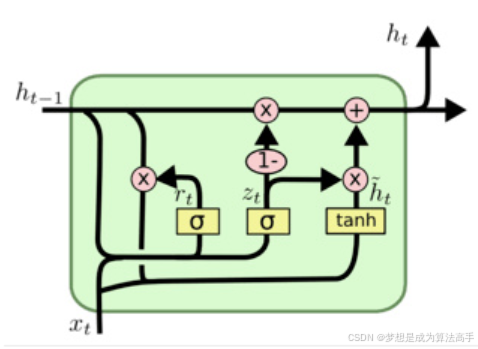
在GRU中门控机制中一共有两个门，下式中的σ表示sigmoid激活函数：

重置门：该门决定了在计算候选隐藏状态时，上一个时间步的隐藏状态中哪些信息应该被重置（遗忘），它接收当前时间步的输入和上一个时间步的隐藏状态，然后输出一个与隐藏状态形状相同的张量，张量中的元素值在0到1之间，计算方法如下：

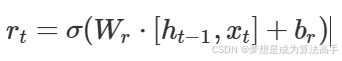
更新门：该门决定了上一时间步的隐藏状态以及当前时间步的候选隐藏状态中信息的更新（保留）比例。它接收当前时间步的输入和上一个时间步的隐藏状态，然后输出一个与隐藏状态形状相同的张量，张量中的元素值在0到1之间，计算方法如下：

在GRU中，有候选隐藏状态的概念，可以视为当前时间步的一个临时的隐藏状态，当前时间步的最终隐藏状态会根据当前时间步的候选隐藏状态以及上一时间步的隐藏状态计算得出，其计算方法如下：

当前时间步的最终隐藏状态的计算方法如下：

GRU与LSTM一样也是通过引入门控机制来有选择地保留信息，从而缓解传统RNN中存在的长程依赖问题，并且在隐藏状态的更新中引入了加性计算，缓解了梯度在各个时间步之间的连乘而导致的梯度消失和梯度爆炸问题，此外，GRU在结构上比LSTM更为简单，GRU的门控机制中只有重置门和更新门两个门，因此它的计算复杂度更低，训练速度更快，但在实际的下游任务中，GRU和LSTM的性能非常接近。

4.1.2 双向GRU

双向GRU（Bidirectional Gated Recurrent Unit，Bi-GRU）是一种改进的GRU，它使用两个独立的GRU来分别处理正序输入序列（从第一个时间步到最后一个时间步）和逆序输入序列从最后一个时间步到第一个时间步），并将正向GRU和反向GRU的各个时间步最后一层隐藏层的隐藏状态逆序拼接起来组成新的隐藏状态（即正向GRU第一个时间步的最后一层隐藏层的隐藏状态与反向GRU最后一个时间步的最后一层隐藏层的隐藏状态在hidden_size维度相拼接，正向在前，以此类推），并作为最后的模型输出（但模型的最后输出的隐藏状态仍然是正向GRU最后一个时间步的最后一层隐藏层的隐藏状态与反向GRU最后一个时间步的最后一层隐藏层的隐藏状态在num_layers维度相拼接，正向在前），这种设计使得Bi-GRU能够同时捕捉过去和未来的上下文信息，从而学习到更全面地长期依赖关系，能够有效地提高模型性能，但参数量和计算复杂度较大。

双向GRU的具体示例如下：

import torch.nn as nn
import torch

def demo():
    # 创建GRU层,前三个参数为input_size, hidden_size, num_layers
    lstm = nn.GRU(3, 4, 2, bidirectional=True)
    # 创建输入张量, 形状为(sequence_length, batch_size, input_size)
    input = torch.randn(3, 1, 3)
    # 双向GRU的num_directions=2，单向GRU的num_directions=1
    # 初始化隐藏状态, 形状为(num_layers * num_directions, batch_size, hidden_size)
    h0 = torch.randn(2 * 2, 1, 4)
    output, hn = lstm(input, h0)
    print('output--->', output.shape, output)
    print('hn--->', hn.shape, hn)

'''
output---> torch.Size([3, 1, 8]) tensor([[[-0.2343, -0.7217, -0.0207, -0.2542, -0.5056, -0.5770, -0.0670,
           0.1820]],
        [[-0.0482, -0.4890,  0.1191, -0.2510, -0.5185, -0.5445,  0.1822,
           0.0414]],
        [[ 0.1062, -0.2590,  0.0822, -0.1805, -0.4589, -0.6113,  0.5441,
          -0.0348]]], grad_fn=<CatBackward0>)
hn---> torch.Size([4, 1, 4]) tensor([[[ 0.6281,  0.0224,  0.5289,  0.3402]],
        [[-0.0106,  0.2983, -0.5434,  0.3410]],
        [[ 0.1062, -0.2590,  0.0822, -0.1805]],
        [[-0.5056, -0.5770, -0.0670,  0.1820]]], grad_fn=<StackBackward0>)
'''

if __name__ == '__main__':
    demo()

4.2 seq2seq模型

4.2.1 传统seq2seq模型

Seq2Seq（Sequence-to-Sequence）模型是一种用于处理序列转换问题的深度学习模型，Seq2Seq模型主要由编码器（Encoder）和解码器（Decoder）两部分组成。

编码器可以使用传统RNN、LSTM或者GRU来实现，编码器会依次处理输入序列中的每一个元素，并按序更新隐藏状态，编码器的主要目的是将输入序列转化成一个上下文向量（context vector）c，上下文向量c通常是编码器所有时间步的最后一层隐藏层的隐藏状态的组合，另一种简单的seq2seq模型的实现是使用编码器最后一个时间步的隐藏状态作为上下文向量c，并将其作为解码器的初始隐藏状态。

解码器也可以使用传统RNN、LSTM或者GRU来实现，解码器会将编码器最后一个时间步的隐藏状态作为解码器的初始隐藏状态，并使用一个特殊的开始符<SOS>作为第一个输入并以自回归（即在生成下一时间步的输出时需要依赖于之前时间步的输出）的形式生成当前时间步的输出，最后在通过一个全连接层和softmax激活函数即可得到当前时间步的预测目标词，解码器会重复上述过程直到生成一个特殊的结束符<EOS>或者达到预先设定的目标序列长度。

Seq2Seq模型的整体结构图如下所示：

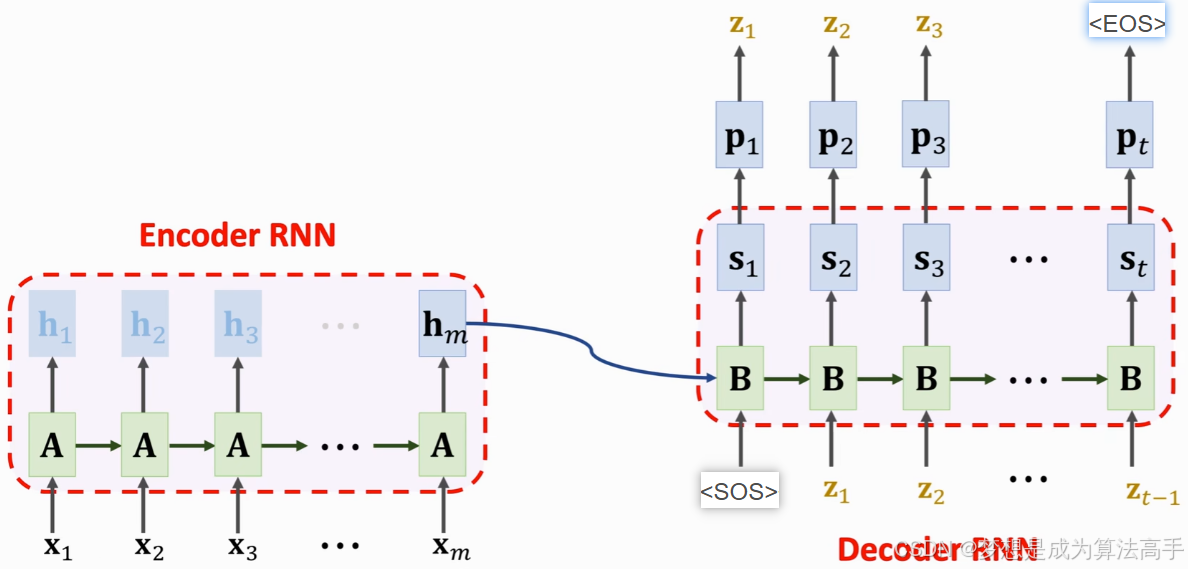
4.2.2 注意力机制

传统seq2seq模型有着以下两个主要的问题：

首先是信息瓶颈问题，编码器需要将整个输入序列的信息压缩到一个上下文向量中，容易导致信息丢失。

其次是长程依赖问题，seq2seq模型底层也是使用传统RNN、LSTM或者GRU来实现，这些模型模型在过长的文本数据中依然难以捕捉长期依赖关系，针对这样的问题，注意力机制被引入到seq2seq模型中。

注意力机制是一种用于增强神经网络模型性能的技术，其本质是模拟人类带有注意力的感知方式，让机器学会去感知数据中的重要和不重要的部分，在传统seq2seq模型中引入注意力机制即可很好地缓解上述两个问题。

注意力机制中通常有Q（query，查询）向量、K（key，键）向量，V（value，值）向量三种向量，seq2seq模型的解码器的上一时间步的隐藏状态将作为Q向量，编码器各个时间步的隐藏状态将作为K、V向量（在带注意力的seq2seq模型中，K向量=V向量），该K、V向量即为原始的上下文向量c，注意力机制的计算是在解码器中进行，编码器通常只负责生成原始的上下文向量c，使用Q向量与K向量进行一定的计算即可得到当前Q向量与各个K向量的注意力分数，常见的注意力分数计算方法有以下三种：

加性注意力：计算公式如下（此时的Q、K向量即为原始的Q、K向量）：

上式的中的Wq、Wk以及vT都是可学习的参数矩阵。

点积注意力：计算公式如下（此时的Q、K向量为经过一个全连接层完成线性变化后得到的Q、K向量）：

缩放点积注意力：计算公式如下（此时的Q、K向量为经过一个全连接层完成线性变化后得到的Q、K向量）：

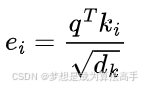
上式中dk表示键向量的长度。

计算得到注意力分数后使用softmax函数进行归一化处理，计算公式如下：

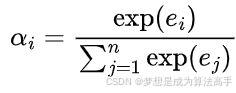
最后，根据注意力权重对各个V向量进行加权求和，即可得到新的上下文向量c，计算公式如下（在带注意力的seq2seq模型中，此时的V向量即为原始的V向量，在transformer模型中，V向量还需要将原始的V向量送入一个全连接层进行线性变化得到最终的V向量）：

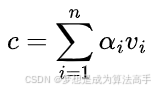
新的上下文向量c后，解码器会根据上一个时间步的隐藏状态、当前时间步的输入和上下文向量c来更新下一时间步的隐藏状态（通常是将三者做拼接后乘以一个权重矩阵，也可以视为将三者一起送入了一个全连接层，然后使用tanh函数激活来得到下一时间步的隐藏状态），最后在通过一个全连接层和softmax激活函数即可得到当前时间步的预测目标词，解码器会重复上述过程直到生成一个特殊的结束符<EOS>或者达到预先设定的目标序列长度。

注意：每个时间步都会使用新的Q、K、V向量来计算新的上下文向量c。

带注意力的seq2seq模型的整体结构框架如下：

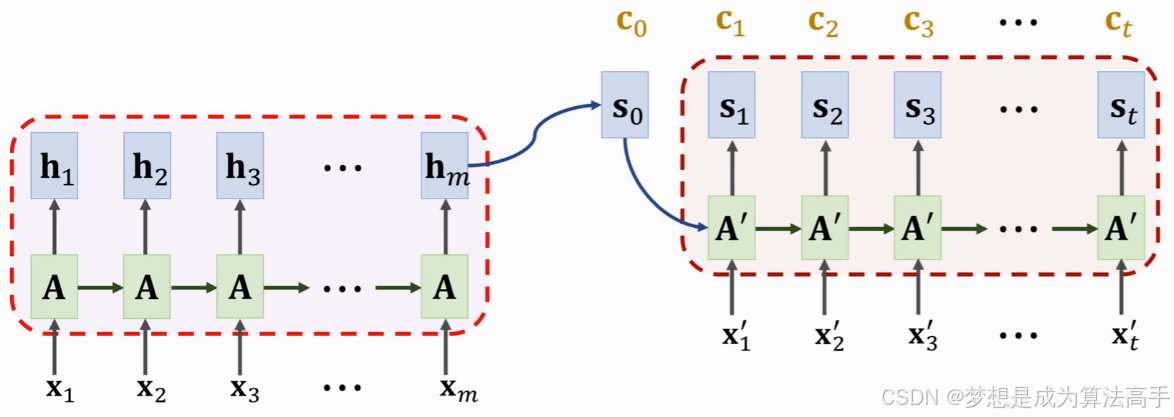
4.2.3 注意力机制的分类

按注意力机制的作用域可以将注意力机制分为以下两类：

软注意力机制：属于一种全局注意力机制，软注意力机制会关注每个V向量并为每个V向量分配一个值域在[0，1]的权重值，而各个权重值的和为1，4.2.2节中介绍的注意力机制的即为一种软注意力机制。软注意力机制能够更加全面地捕捉V向量的整体信息，但计算量较大。

硬注意力机制：属于一种局部注意力机制，硬注意力机制会关注部分V向量并通过某种策略（如随机采样或选择注意力分数最大的V向量）来选取需要关注的V向量（可以视为为每个V向量分配一个非0即1的权重值）。硬注意力机制的优势在于可以节省一定的计算资源，但硬注意力机制的注意力分数的计算过程通常是不可微的，导致无法使用反向传播算法训练模型，往往需要借助强化学习等特殊的训练方法来训练模型。

4.2.4 Teacher Forcing

在Seq2Seq模型中，解码器会以自回归的形式生成当前时间步的输出，如果解码器在上一个时间步生成了错误的输出yt−1，那么这个错误会传递到当前时间步，导致误差的累积，影响模型的性能。

Teacher Forcing是一种在训练Seq2Seq模型时常用的训练策略，该策略的核心思想是在解码器的训练过程中，使用当前时间步真实的目标序列（Ground Truth）作为解码器的输入，而不是使用解码器上一个时间步自己生成的输出。

Teacher Forcing可以加速模型的收敛、提高训练稳定性，但在测试阶段时，解码器只能使用自己的预测输出作为输入，而在训练阶段时，解码器的输入是真实的目标序列，这种训练阶段和测试阶段的不一致性可会导致模型在测试时表现不佳。

使用Scheduled Sampling可以有效地改进Teacher Forcing，Scheduled Sampling是指在训练阶段以一定的概率随机选择使用真实的目标序列或模型自身的预测输出作为输入，而随着训练的进行，逐渐降低使用真实的目标序列的概率，让模型更多地学习如何处理自己的预测结果，从而缓解训练阶段和测试阶段的不一致性所导致的问题。

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐