64. 最小路径和

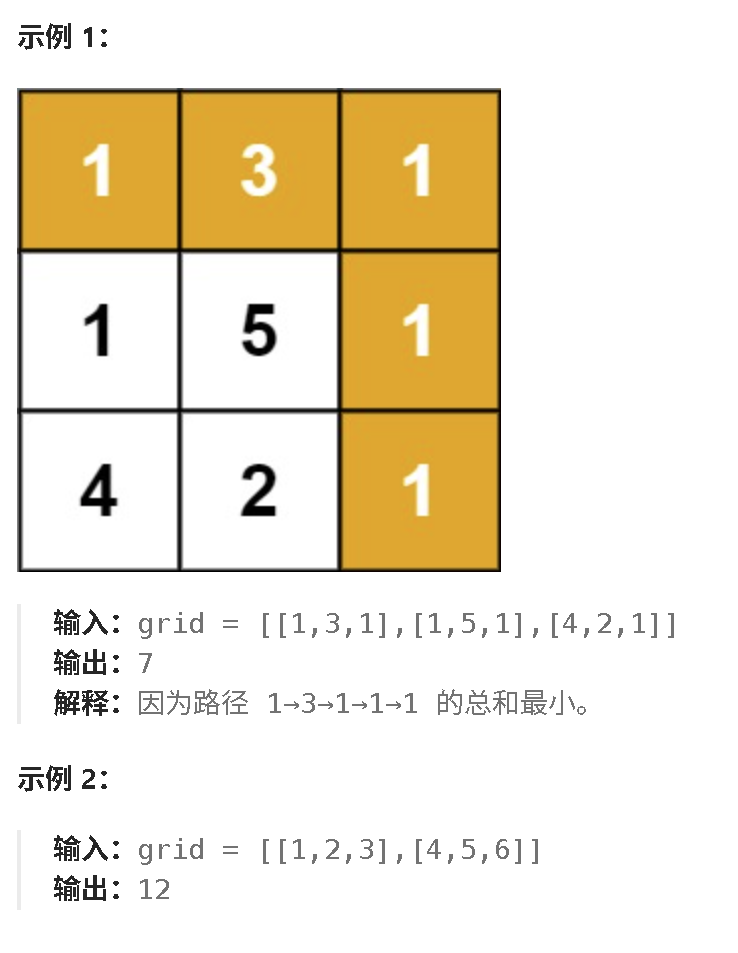
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200

下面我们还是用“填表格”的直观方式来理解这道**“最小路径和”**题的动态规划解法。

---

一、问题回顾

给定一个 $m\times n$ 的网格 grid，格子里都有非负整数。机器人从左上角出发，每次只能向右或向下走一步，沿途把经过格子的数字加起来，问到达右下角能拿到的**最小“总和”**是多少？

---

二、通俗易懂的思路

1. 定义「打分表」

我们新建一个大小相同的表 dp，dp[i][j] 表示「到达格子 $(i,j)$ 时，能拿到的最小路径和」。

2. 边界初始化

• 起点 $(0,0)$：dp[0][0] = grid[0][0]。

• 第一行（只能一直向右走）：

  $$dp[0][j]=dp[0][j-1]+grid[0][j]$$

• 第一列（只能一直向下走）：

  $$dp[i][0]=dp[i-1][0]+grid[i][0]$$

3. 状态转移

对于其余格子 $(i,j)$，最后一步要么从上面下来，要么从左边过来，因此取两者中的「更小」：

$$dp[i][j]=\min (dp[i-1][j],dp[i][j-1])+grid[i][j].$$

4. 举例填表

以示例一 grid = [[1,3,1],[1,5,1],[4,2,1]] 为例：

原始网格：

	j=0	j=1	j=2
i=0	1	3	1
i=1	1	5	1
i=2	4	2	1

我们填 dp：

1. dp[0][0]=1

2. 第一行：

   • dp[0][1] = 1 + 3 = 4
   • dp[0][2] = 4 + 1 = 5

3. 第一列：

   • dp[1][0] = 1 + 1 = 2
   • dp[2][0] = 2 + 4 = 6

4. 其余格子：

   • dp[1][1] = min(dp[0][1]=4, dp[1][0]=2) + 5 = 2+5 = 7
   • dp[1][2] = min(dp[0][2]=5, dp[1][1]=7) + 1 = 5+1 = 6
   • dp[2][1] = min(dp[1][1]=7, dp[2][0]=6) + 2 = 6+2 = 8
   • dp[2][2] = min(dp[1][2]=6, dp[2][1]=8) + 1 = 6+1 = 7

最终 dp 表：

	0	1	2
0	1	4	5
1	2	7	6
2	6	8	7

右下角 dp[2][2]=7，即为答案。

---

三、代码实现

下面给出 C++ 和 Python 两种基于上述思路的实现，时间复杂度 $O(mn)$、空间复杂度 $O(mn)$。

---

C++ 代码

#include <bits/stdc++.h>
using namespace std;

int minPathSum(vector<vector<int>>& grid) {
    int m = grid.size();
    int n = grid[0].size();
    // dp[i][j]：到达 (i,j) 的最小路径和
    vector<vector<int>> dp(m, vector<int>(n, 0));
    dp[0][0] = grid[0][0];
    // 第一行
    for (int j = 1; j < n; ++j) {
        dp[0][j] = dp[0][j-1] + grid[0][j];
    }
    // 第一列
    for (int i = 1; i < m; ++i) {
        dp[i][0] = dp[i-1][0] + grid[i][0];
    }
    // 剩余格子
    for (int i = 1; i < m; ++i) {
        for (int j = 1; j < n; ++j) {
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
        }
    }
    return dp[m-1][n-1];
}

int main() {
    int m, n;
    cin >> m >> n;
    vector<vector<int>> grid(m, vector<int>(n));
    for (int i = 0; i < m; ++i)
        for (int j = 0; j < n; ++j)
            cin >> grid[i][j];
    cout << minPathSum(grid) << "\n";
    return 0;
}

---

Python 代码

from typing import List

def min_path_sum(grid: List[List[int]]) -> int:
    m, n = len(grid), len(grid[0])
    # 创建 dp 表，与 grid 同尺寸
    dp = [[0] * n for _ in range(m)]
    dp[0][0] = grid[0][0]
    # 第一行
    for j in range(1, n):
        dp[0][j] = dp[0][j-1] + grid[0][j]
    # 第一列
    for i in range(1, m):
        dp[i][0] = dp[i-1][0] + grid[i][0]
    # 剩余格子
    for i in range(1, m):
        for j in range(1, n):
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
    return dp[m-1][n-1]

if __name__ == "__main__":
    m, n = map(int, input().split())
    grid = [list(map(int, input().split())) for _ in range(m)]
    print(min_path_sum(grid))

---

四、结题思路小结

1. 状态：dp[i][j] 表示到达格子 $(i,j)$ 时路径和的「最小值」。

2. 初始化：

   • dp[0][0] = grid[0][0]
   • 第一行只能从左边来，第一列只能从上面来。

3. 状态转移：

   $$dp[i][j]=\min (dp[i-1][j],dp[i][j-1])+grid[i][j].$$

4. 答案：dp[m-1][n-1]。

这样，机器人走到每个格子时都“累加”了从起点到这里的最小和，最后读出终点的值就是全程的最小路径和。简单、清晰，一步步填表就能算出来。