模糊综合评价模型

模糊集合的概念：用来描述模糊性质的集合，例如高，年轻等。
模糊集合的基本属性：不存在互斥性与确定性。
模糊集合的刻画：隶属函数(membership function)。例如小明升高170cm，则小明可以属于高个子集合，也可以属于矮个子集合。隶属函数可以用于刻画小明究竟属于哪一个模糊集合，可以理解为属于哪一个模糊集合的概率大，但为了严谨，这里称之为隶属度。
模糊集合的表示方法（已知论域，模糊集合为A，每一个元素的对于这模糊集合的隶属度记为）：
- Zadeh表示法 $A=\frac{A(x_1))}{x_1}+\frac{A(x_2)}{x_2}+...+\frac{A(x_n)}{x_n}$
- 序偶表示法 $A=\{(x_1,A(x_1)),(x_2,A(x_2)),...(x_n,A(x_n))\}$
- 向量表示法 $A=\{A(x_1),A(x_2),...,A(x_n)\}$

隶属函数的确定方法

由模糊数学的基本概念可知，对研究结果起至关作用的因素是隶属函数，而每一个模糊集合没有一个确定的隶属函数，故需要对确定隶属函数做出严格的规定。通常有如下三种方法确定一个较好的隶属函数：

模糊统计法

原理：找多个人对同一个模糊概念进行描述，用隶属的频率去定义隶属函数

以确定模糊集合“年轻”的隶属函数举例，定义人的年龄为论域 $U$ ，调查n个人，让这n个人仔细考虑“年轻”的含义，给出他们认为的最适合的年龄区间，对于任意一个确定的年龄，若n个人中有m个人给出的区间包含25，则称m/n为25岁属于年轻这一模糊集合的隶属频率，以此类推可以确定论域中的隶属频率。根据大数定理，当样本n的取值较大时，可认为隶属频率即隶属度，进而可以得到隶属函数。

该方法较为客观，并且通过该方法确定的隶属函数有较高的可靠性。缺点是该方法耗时较久。

指派法

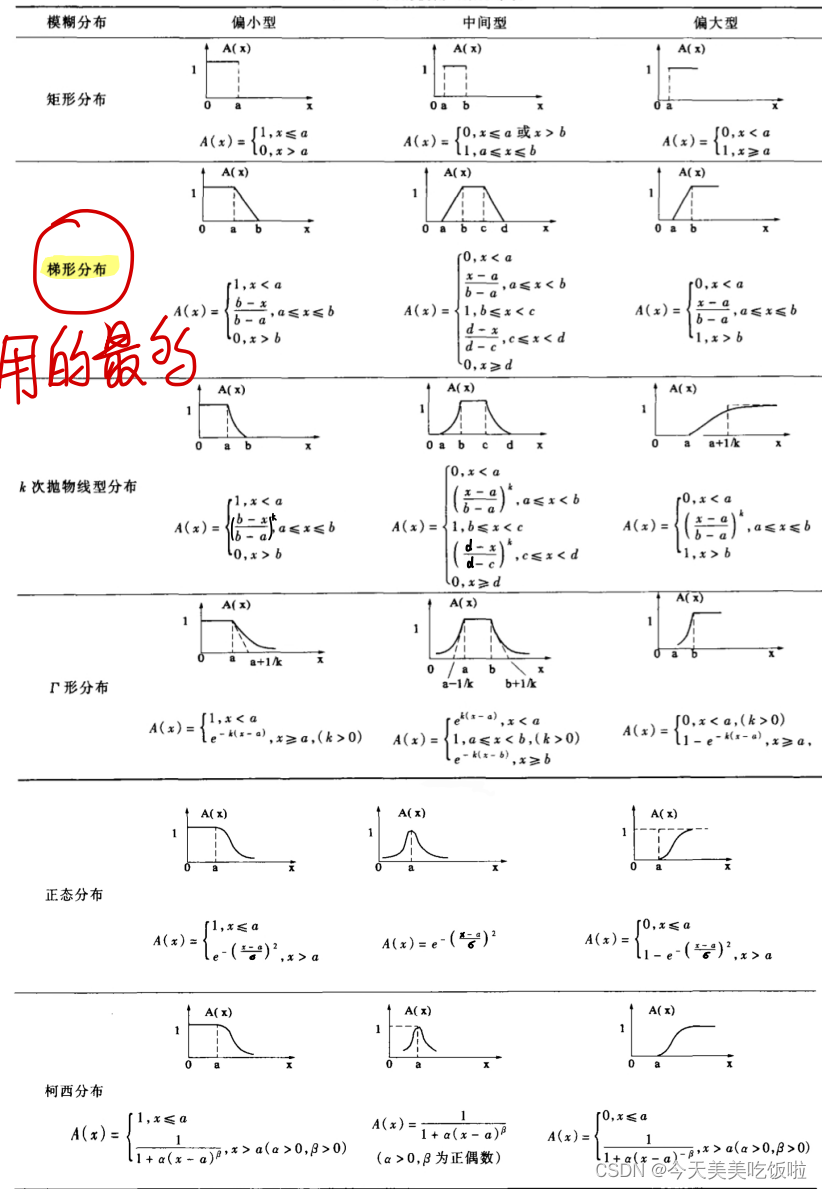
根据模糊集合是最小型，中间型还是最大型，选择一个分布作为隶属函数

模糊综合评价

当因素集合中的个数较少，不超过5个，采用一级模糊评判；如果较多则采用多级模糊评判

一级模糊评判分析步骤

确定因素集

对于一个确定的评价问题，首先明确从哪些方面进行评判，即因素集。记为 $U=\{u_1,u_2,...,u_n\}$

确定评语集

对于一个确定的评价问题，我们需要分清楚评价对象的评价结果，如优良差等，或者是方案选择。记为 $V=\{v_1,v_2,...,v_m\}$

确定权重集

对于一个确定的评价问题，评价指标的重要性通常是不同的，即代表不同的权重。该权重集记为 $A=\{a_1,a_2,...,a_n\}$ 。

显然权重集与因素集的维度相同。

得到模糊综合判断矩阵

由模糊统计法或指派法，对于每一个指标 $u_i$ ，计算出该指标属于评语集这个模糊集合中每个元素的隶属度。称为对指标 $u_i$ 的评判，记为 $R_i=[r_{i1},r_{i2},...,r_{im}]$ 。

依次类推，对所有指标进行评判，得到所有的 $R_i$ 。将其以列向量的形式拼接而成，可以得到最终的模糊综合判断矩阵，即

综合评判

记 $B=AR$ ，显然B是一个与评语集同维度的行向量，其元 $b_i$ 的物理意义为评价对象的最终结果在模糊集合中第i个元素的隶属度。

由最后的隶属度向量可以得到最后的评判结果属于评语集中的哪一个元。

多级模糊综合评判分析步骤

如果指标较多，我们可以采取多级模糊综合评判方法

多级评判和一级评判大同小异，其最主要的区别在于模糊综合评判矩阵的求法。

以学生评价奖学金为例，因素集的层次结构如下，并且含有对应的权重。

并假设评语集V={一等奖学金，二等奖学金，三等奖学金}

根据一定的方法得到专业课成绩指标的评判为[0.8 0.2 0]，非专业课成绩指标的评判为[0.7 0.3 0]

将其拼接称一级指标学习成绩的评判矩阵 $R1'=\begin{pmatrix} 0.8 \quad 0.2 \quad 0\\ 0.7 \quad 0.3 \quad 0 \end{pmatrix}$

记 $R_1=A_1R_1'=[0.6 \quad 0.4]\begin{bmatrix} 0.8 \quad 0.2 \quad 0\\ 0.7 \quad 0.3 \quad 0 \end{bmatrix}=[0.76\quad 0.24\quad 0]$ 。

向量结果的意义为，只从学习成绩这一个指标来看，该生隶属于一等奖学金的隶属度为0.76，二等奖学金的隶属度为0.24，三等奖学金的隶属度为0.

同理可以得到分别只从竞赛成绩，个人荣誉，志愿服务一个指标，隶属于评语集的隶属度向量 $R_2,R_3,R_4$ ，最后拼接为模糊综合评判矩阵R。分析步骤同一级模糊综合评判。

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐