一、问题重述

1.1问题背景

得益于数字技术的应用，在工程、科学以及数学领域，常见的傅里叶变换都是采用离

散傅里叶变换（Discrete FourierTransform），以下简称DFT。例如，在处理通信信号时，

通常采用DFT实现信号的正交频分复用系统的时频域变换。同时，在信道估计领域，也需要利用DFT和IDFT（逆DFT），对信道估计结果进行时域降噪处理。

在芯片设计领域，DFT计算的硬件复杂度受其算法复杂度和数据元素取值范围影响。算法复杂度越高、数据取值范围越大，其硬件复杂度就越大。为降低DFT的硬件复杂度，在目前的实际应用中，一般采用快速傅里叶变换[1]（Fast FourierTransform），以下简称

FFT。随着无线通信技术的演进，对于FFT的需求量越大则导致实现的开销越大，因此，为进一步降低芯片资源开销，可将DFT矩阵分解成整数矩阵连乘的形式。

 

二、模型假设

（1）假设RMSE和C之间存在一个权衡关系，即RMSE越小，C越大，反之亦然；

（2）假设DFT矩阵 （3）假设DFT矩阵	F 的分解方案是稳定的，即不受其他因素干扰； N
	F 的分解方案是可实现的，即分解后的矩阵 N	A 可计算和存储。 K

三、符号说明

符号设定	符号说明
C q L N    p w b  Q IN	硬件复杂度
	分解后的矩阵	A 中元素的取值范围 k
	复数乘法的次数
	DFT矩阵		F 的采样点数 N
	实值矩阵的缩放因子 排列矩阵 权重 偏差 学习率 任意矩阵 N 阶单位矩阵

4.3基于稀疏矩阵分解模型采用分治算法

分治的策略是DFT的关键，利用分治策略[5]，可以将一个规模为N 的大问题分解成K个小规模子问题，各子问题之间相互独立且与原问题性质相同。在处理复杂问题时，往往通过小问题的解合并成大规模问题的解，从而自上而下逐步求出原问题的解。

          采用分治算法解决问题往往具有以下特征：
          （1）解决问题时，问题的计算复杂度往往是随着问题的规模增加而增加。当原问题规模较大不易解决时，发现原问题若能缩小到一定程度即可容易解决；
          （2）当原问题可以分解为若干个规模较小的子问题，且子问题之间相互独立、互不影响，求解的过程与原问题相关且近似时，即可采用分治思想，反映了递归思想的应用；      （3）利用分治算法解决问题的关键在于，能将子问题的求解合并后得到原问题的解； ➢  蝶形运算的原理
          在使用分治算法时，会使用蝶形运算，其具体原理[6]如图所示：

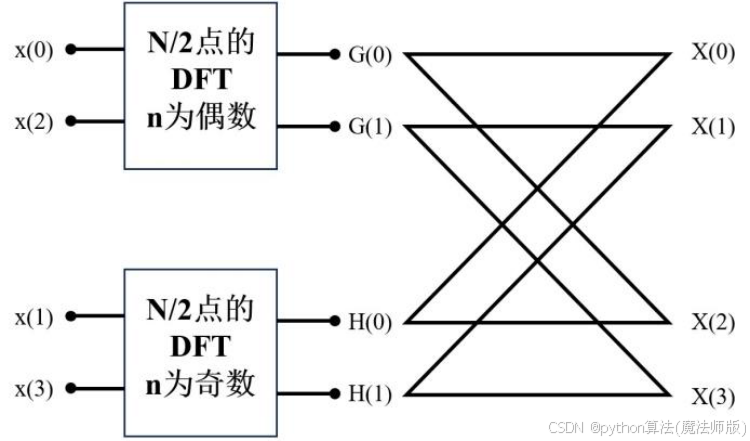
图  2   蝶形运算原理图

分治算法的一般步骤

图  3 分治算法步骤流程图

 

 

 

基于DFT矩阵低秩近似模型采用梯度下降算法

➢  梯度下降的目的
          大多数的机器学习模式都会存在损失函数，通常也会用损失函数来衡量机器学习模式

的精确度。一般来说，损失函数的值越小，模型的精确度就越高。因此，若要提高机器学

习模型的精准度，即尽可能的降低损失函数的值，故而采用梯度下降的方法。所以，梯度下降的目的，就是为了最小化损失函数。

➢  梯度下降的原理
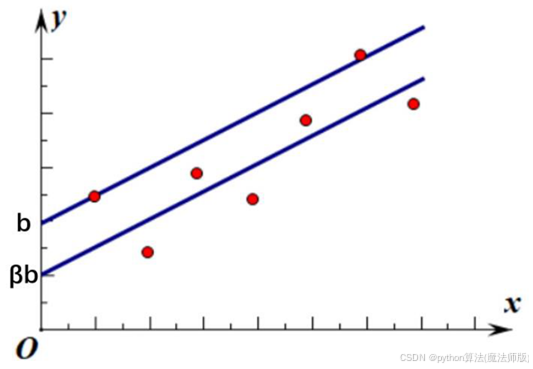
          寻找损失函数的最低点，可以通过求出函数导数的值，从而找到函数下降的方向或最低点[9]。损失函数中一般有两种参数，一种是控制输入信号量的权重（weight，简称w），

另一种是调整函数与真实值距离的偏差（Bias，简称b），通过梯度下降的方法，不断地调整权重w与偏差b，使得损失函数的值变得越来越小。

假设某损失函数，权重w目前所在位置为A点，此时若求出A点的梯度dL dw，便可知若向某方向运动，损失函数的值便可变得更小。通过计算梯度，可知w的移动方向，也可知道何时会到达最低点。若对于问题中出现多个权重的情况，对于每一个样本数据，都

可求出一个权重的梯度。此时，则需要将各个样本数据的权重梯度相加，并求出它们的平均值，用该平均值作为样本整体的权重梯度。

 

九、模型评价

9.1模型优点

          （1）处理规模较大的问题时，采用分治算法，可以极大地提高运算效率；
          （2）最小二乘法求得的结果唯一，求解方便且具有较好的解析性质；
          （3）利用最小二乘法能简便地求得未知数据，并使得求得的数据与实际数据之间的误差平方和最小；
          （4）对于某些最小二乘无法计算全域唯一优解的情况，梯度下降法仍可有效进行最小值点的寻找。

9.2模型缺点

          （1）采用分治算法解决问题时，若原问题分解出的若干子问题之间不是相互独立的，则会影响分治的效率，此时采用动态规划更好；
          （2）利用梯度下降算法时，并非所有损失函数都是严格凸函数，要尽量避免最小值点或鞍点陷阱。

代码输入：

%% 处理矩阵

N=8;

FN=zeros(N);

A=zeros(N);

  for i=1:N

  for j=1:N

FN(i,j)=N^(-1/2)*cos(2*pi*(i-1)*(j-1)/N)-N^(-1/2)*sin(2*pi*(i-1)*(j-1)/N)*1i;

  if cos(2*pi*(i-1)*(j-1)/N)>0.01   

  A(i,j)=A(i,j)+1;

  elseif cos(2*pi*(i-1)*(j-1)/N)<-0.01   

  A(i,j)=A(i,j)-1;

  else

  A(i,j)=0;

  end

  if sin(2*pi*(i-1)*(j-1)/N)<-0.01

  A(i,j)=A(i,j)+1i;

  elseif sin(2*pi*(i-1)*(j-1)/N)>0.01   

  A(i,j)=A(i,j)-1i;

  else

  A(i,j)=A(i,j);

  end

  end

  end

  % 最小二乘

  syms x;

  fs=0;

  for i=1:N

  for j=1:N

  fs=fs+abs(FN(i,j)-x*A(i,j))^2;

  end

  end

f=@(x)abs(2^(1/2)/4 - x + 493978371506187i/1267650600228229401496703205376)^2 + 2*abs(x*1i - (2^(1/2)*1i)/4 + 493978371506187/2535301200456458802993406410752)^2 + 15*abs(x - 2^(1/2)/4)^2 + 2*abs(2^(1/2)/4 - x +
6147286400965883i/20282409603651670423947251286016)^2 + 2*abs(x*1i - (2^(1/2)*1i)/4 + 6147286400965883/40564819207303340847894502572032)^2 + 3*abs(2^(1/2)/4 - x + 7025470172532437i/162259276829213363391578010288128)^2 + 2*abs(2^(1/2)/4 - x + 7025470172532437i/81129638414606681695789005144064)^2 + abs(2^(1/2)/4 - x +
7025470172532437i/40564819207303340847894502572032)^2 + 2*abs(x*1i - (2^(1/2)*1i)/4 + 7025470172532437/324518553658426726783156020576256)^2 + 4*abs(2^(1/2)/4 - x + 164659457168729i/1267650600228229401496703205376)^2 + 2*abs(2^(1/2)/4 - x +
164659457168729i/633825300114114700748351602688)^2 + 4*abs(x*1i - (2^(1/2)*1i)/4 + 

代码输入：

          N=8;
          B=N^(-1/2)*[1,0,0,0,1,0,0,0;0,1,0,0,0,2^(-0.5)*(1-1j),0,0;0,0,1,0,0,0,-1j,0;0,0,0,1,0,0,0,2^(-0.5)*(-1-1j);1,0,0,0,-1,0,0,0;0,1,0,0,0,-2^(-0.5)*(1-1j),0,0;0,0,1,0,0,0,1j,0;0,0,0,1,0,0,0,-2^(-0.5)* (-1-1j)];

A=zeros(N);

  for i=1:N

  for j=1:N

  if real(B(i,j))>0.3

  A(i,j)=A(i,j)+2;

  elseif real(B(i,j))>0.01

  A(i,j)=A(i,j)+1;

  elseif real(B(i,j))>-0.01

  A(i,j)=A(i,j);

  elseif real(B(i,j))>-0.3

  A(i,j)=A(i,j)-1;

  else   

  A(i,j)=A(i,j)-2;

  end

  if imag(B(i,j))>0.3

  A(i,j)=A(i,j)+2i;

  elseif imag(B(i,j))>0.01   

  A(i,j)=A(i,j)+1i;

  elseif imag(B(i,j))>-0.01

  A(i,j)=A(i,j);

  elseif imag(B(i,j))>-0.3

  A(i,j)=A(i,j)-1i;

  else   

  A(i,j)=A(i,j)-2i;

  end

  end

  end

  %% rmse公式

  syms t;

  fs3=0;

  for i=1:N