---

📘 吴恩达机器学习 - 代价函数（Cost Function）全解析

“代价函数不是模型的一部分，而是我们判断模型是否学习得‘像人一样’的重要标尺。”

---

一、什么是代价函数？🧠

在监督学习中，模型的任务是“从输入预测输出”，而我们需要有一个“评价标准”，来衡量模型当前的预测表现到底好不好。

这就引出了「代价函数（Cost Function）」，它的本质是一个：

衡量模型输出与真实标签之间差距的函数。

严谨的说： 

在所有监督学习问题中，目标是通过已有样本构造一类函数 hθ(x)h_\theta(x)hθ​(x)，使其在未见数据上具有良好的泛化能力。显然，需要一个度量指标来判断模型在已知样本上的“表现”，即衡量预测值 hθ(x(i))h_\theta(x^{(i)})hθ​(x(i)) 与真实值 y(i)y^{(i)}y(i) 之间的偏离程度。

该指标即为代价函数（Cost Function），又称损失函数，其最常用形式为：

对于线性回归，我们通常使用的是 均方误差（Mean Squared Error, MSE），定义如下：

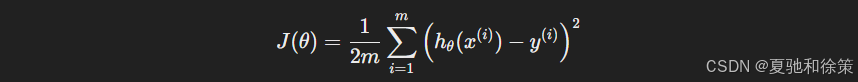
其中：

• mm：样本总数

• hθ(x)h_\theta(x)：模型预测值

• yy：真实值

• θ\theta：模型参数

 这是机器学习中线性回归模型的典型形式，对应于统计学中的最小二乘准则。（高中都学过了）

---

二、代价函数的直观理解 👁

从直觉上讲，它其实就是告诉你：模型画出来的“线”离数据点到底有多远。

• 每一个样本点的“预测误差”是 hθ(x)−yh_\theta(x) - y

• 我们平方这个误差（避免正负抵消）

• 然后对所有样本求和再平均（为了公平评估整体误差）

你可以把它想象成每次试题做错了多少分，然后把所有题的扣分加起来求平均。

📌 所以说，代价函数越小，模型越准确。

2. 数学结构分析：代价函数的解析几何属性

若假设：

则 J(θ)J(\theta)J(θ) 的数学形式是变量为 θ0,θ1\theta_0, \theta_1θ0​,θ1​ 的二次型函数，其几何图像为三维空间中的椭圆抛物面（elliptic paraboloid）。

其性质如下：

• 极小值唯一，位置由 ∇J=0\nabla J = 0∇J=0 解确定；

• 水平截面（z=cz = cz=c）为椭圆；

• 拥有良好的凸性（convexity），梯度下降法可全局收敛。

---

三、为什么要除以 2？✳️ 数学技巧背后的理由

在定义 MSE 的时候，我们常常会看到它前面多了一个 12\frac{1}{2}，变成：

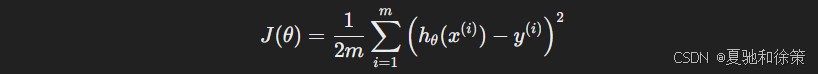
这是为什么呢？

✅ 原因是：为了推导梯度下降的导数更简洁优雅。

如果没有这个 12\frac{1}{2}，求导后会出现一个额外的 2：

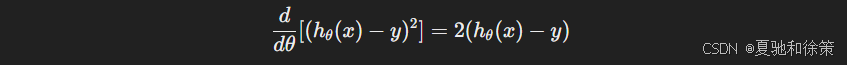
消去了前导系数 2，使得梯度表达式简洁。

• 并非数学严谨性的需求，而是为后续推导的对称性与简洁性服务。这种“刻意的系数设计”，本质是工程数学中的一种优化手段，称为：

📌 归一化常数技巧（Normalization constant trick）

换句话说，多了这个 2 会让梯度更新公式变臃肿。为了简化后续推导，提前把这个 2“归一化”了，这体现了一个常见的数学计算技巧：归一化常数（Normalization Constant），类似高数中我们常见的“为了好看除一个 2”。

---

四、可视化代价函数 🌐

在机器学习中，可视化是理解复杂函数的一把钥匙。

吴恩达在课程中用了两个非常形象的三维图来展示代价函数 J(θ0,θ1)J(\theta_0, \theta_1) 的形状：

1. 3D 曲面图（Surface Plot）
   显示了整个参数空间中，代价函数的变化趋势。形如碗状凸函数（bowl-shaped）。

展示函数 J(θ0,θ1)J(\theta_0, \theta_1)J(θ0​,θ1​) 的整体形状。直观可见的特征是：

• 图像如同一碗；

• 极小点位于碗底；

• 表面平滑连续，利于梯度优化。

1. 等高线图（Contour Plot）
   类似“航拍视角”从上往下看，就像地图的等高线一样，更清晰展示最小值位置和梯度下降路径。

将三维抛物面垂直投影到 θ0−θ1\theta_0-\theta_1θ0​−θ1​ 平面。特点：

• 每一条曲线对应相同的 JJJ 值；

• 梯度下降过程可以在该图中可视为“碗中小球滚落”；

• 可清晰观察优化路径是否震荡、收敛。

📌 这两者结合后，非常有助于我们理解为什么梯度下降可以“不断靠近最低点”。

在课程中，Ng 使用一个关于房价预测的二元线性回归模型：

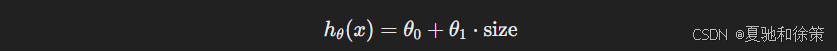
通过连续迭代更新 θ\thetaθ，在等高线图中画出路径，最终趋于代价函数最小值。该图形不仅直观展示了优化效果，也揭示了学习率设置对收敛行为的影响。

• 学习率过大：路径震荡，甚至发散；

• 学习率合适：路径平滑收敛。

---

五、可视化的例子 🖼

来看吴恩达讲的两个图：

✅ 曲面图 Surface Plot

• xx 轴为 θ0\theta_0

• yy 轴为 θ1\theta_1

• zz 轴为代价函数 J(θ)J(\theta)

• 图像是一个向下开的碗型，表示只存在一个最小值（全局最优）

✅ 等高线图 Contour Plot

• 就像坐飞机、火箭从高空鸟瞰这个碗

• 每一条线表示代价函数的“同一高度”，中心就是最优解

• 在后面讲解梯度下降时，这个图尤其重要，因为它能可视化下降路径！

🧠 如果你学习过二次函数、偏导和极值点，看到这些图一定倍感亲切：这正是应用“凸函数”和“泰勒展开”的地方。

---

六、工程与数学的桥梁 🔗

📌 学术上我们定义代价函数，是为了严谨建模；
📌 工程上我们使用代价函数，是为了指导模型优化。

代价函数就是这样一个连接理论与工程实践的桥梁。

它不仅帮我们：

• 明确目标（什么样的模型是“好”的？）

• 衡量当前效果（还差多少？）

• 指引优化方向（朝哪个方向变好？）

更重要的是，它让机器具备了“学习能力”的度量机制。

---

七、 小结：从代价函数到优化的逻辑闭环

代价函数的设计不是孤立的，它是整个学习框架中的关键一环：

环节	数学构件	作用
模型假设	hθ(x)h_\theta(x)hθ​(x)	建立输入与输出之间的函数映射
误差评估	J(θ)J(\theta)J(θ)	衡量预测结果与真实值的偏差
最优化方法	梯度下降	通过不断调整 θ\thetaθ 逼近最优解

代价函数在其中起到承上启下的作用，是从建模到训练之间唯一的评估指标。

---

七、总结一句话 ✅

代价函数，是机器学习中最关键的“目标函数”，它不仅衡量模型表现，也引导模型进化方向，是“智能”的量化基础。

在机器学习的线性回归中，代价函数不仅是误差的度量器，更是整个模型从假设到优化的桥梁。其形式虽简，其意义却深，贯穿着数学结构、几何直觉与工程实现的三重逻辑。

---