摘要

识别房屋内人类日常生活活动是建立房屋耗电模型的有效工具，也是监测居民健康状况的良好指标。智能家居中的活动识别问题已经在一些研究中得到了广泛的解决。本文基于机器学习隐马尔可夫模型，提出了一种在LabVIEW环境下开发的交互式工具，该工具具有图形化用户界面，可以对日常生活活动进行建模。在概述了在当前人类活动中使用这个模型的优势之后，我们检验了相关的科学问题如何通过机器学习找到解决方案。因此，应用基于隐马尔可夫模型的方法，我们提出和评估两组实验数据。通过与其他日常生活活动识别方法的比较，我们发现隐马尔可夫模型具有非常令人满意的识别性能，以及我们开发一个用户友好的图形化界面的可能性。这项工作为专门用于监测人类日常生活活动和/或管理配备了非侵入式传感器的智能家居内的用电的应用开辟了道路。

关键词

日常生活活动；隐马尔可夫模型；LabVIEW；机器学习；传感器数据；智能家居

一、介绍

通过推广使用可再生能源，并结合鼓励减少能源消费（特别是家庭能源消费）的政策，能源资源的多样化以及人类日常生活活动的监测和管理最近通过一些研究得到了解决，如[5,10,32]。在这种背景下，有越来越多的人关注和研究智能家居，智能家居最初是为了增加居民的舒适度或提供老年人健康状况的指标。但是，正如这一贡献主要关注的那样，在专门研究智能家居人类活动识别系统的研究中，第二个优先目标应该是开发新的方法，以便在可持续性的背景下为减少温室气体排放和减少能源账单作出有效贡献。在这些研究中，我们特别引用[16，33，34]中报告的研究，这些研究涉及实时和/或计划监测能源消耗的新发展和综合解决方案，以便根据其可用性、价格和家庭居民期望的舒适度对其进行优化。由于家庭中的能源消耗与个人的习惯密切相关[12]，借助传感器网络（最终，利用物联网（IoT）提供的多种可能性，如[1、2、23]中所述），通过使房屋智能化来模拟人类在房屋中的行为是很有趣的，为了了解和预测（可能是远程）居民的活动，而不需要他们直接与系统进行物理交互以保护他们的隐私。因此，我们有兴趣建立一个可靠且实用的模型来远程识别人类在家中的日常生活活动，如烹饪、吃饭、睡觉等等。然而，基本的经典方法仅通过上下文方法解决这个问题，而不是通过情景方法。事实上，基于用户和应用程序的上下文模型是由专家用自顶向下的方法指定和实现的。在这种方法中，专家手动将传感器、上下文模型和预期服务静态地关联起来。但是，由于居民的新行为，场景可能出现或消失，因此必须融入智能环境。因此，自顶向下方法中的静态上下文模型是不够的，特别是如果我们考虑到很大的容量以适应当前由智能环境提供的能量监测和管理系统的用户的需要。

因此，人类活动识别研究的目标是开发自下而上的自动学习方法，以实现自主系统，使其能够在智能环境中随用户的行为和需求而进化。这相当于用情境模型替换上下文模型。这种情况，模型依赖于机器学习方法中开发的分类和回归方法所获得的结果，这些方法已经在医学等各个应用领域得到应用[6，9，17–21，26]。这些开发情境模型的方法和途径也可以作为智能家庭能源系统管理的基本工具（参见参考文献[8，13]）。

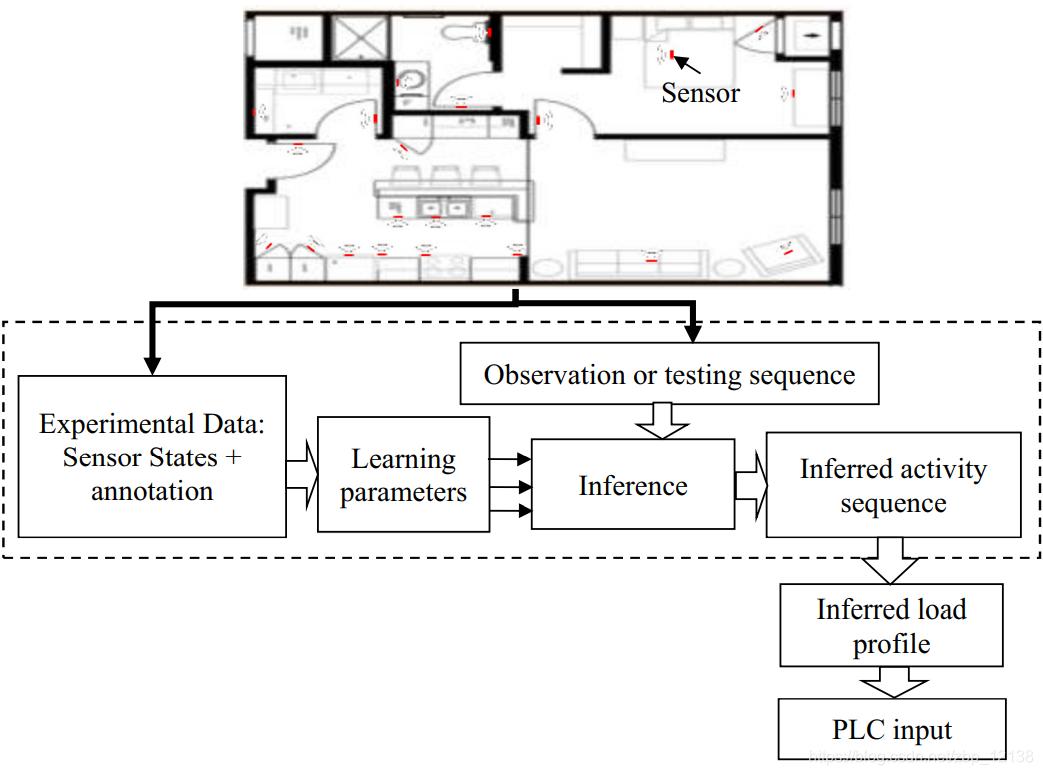
在目前的贡献中，所开发的系统涉及一个基于隐马尔可夫模型（HMM）的机器学习模型。该系统允许监控与能源消耗相关的日常生活活动。它是在提供交互式图形用户界面（GUI）的LabVIEW环境下实现的。这个原始系统的目的是在不损害居民隐私的情况下，从位于房屋各个部位的传感器数据实时预测居民的日常生活活动。在达到通常的预测和日常监测模式之前，将使用一个基于上游记录的实际实验数据集的程序，以便对模型进行参数化，此外，还将允许测试和验证全球应用程序的性能和可靠性。

在目前的研究中，遵循这一程序，以发达国家的标准和相当普遍的研究案例为例进行验证。图1的框图展示出了具有传感器位置的标准家庭以及全局方法。

图1 标准住宅的平面图和所考虑的自下而上建模方法的概要图

在描述了模型、方法及其相关的图形用户界面和一组实验数据之后，我们将在下面给出获得的验证结果。

由于开发的应用主要涉及能源消耗的优化管理，并且如图1所示，在允许满足检测室内人类活动的三种类型的传感器中，我们将只考虑直接的环境组件和基础设施系统，例如实时提供的电力系统、电力消耗的数据。为了获取信息，第三种传感器技术集成了居民佩戴的便携式设备，以监测人的生理状态或运动。

二、方法和LabVIEW实现

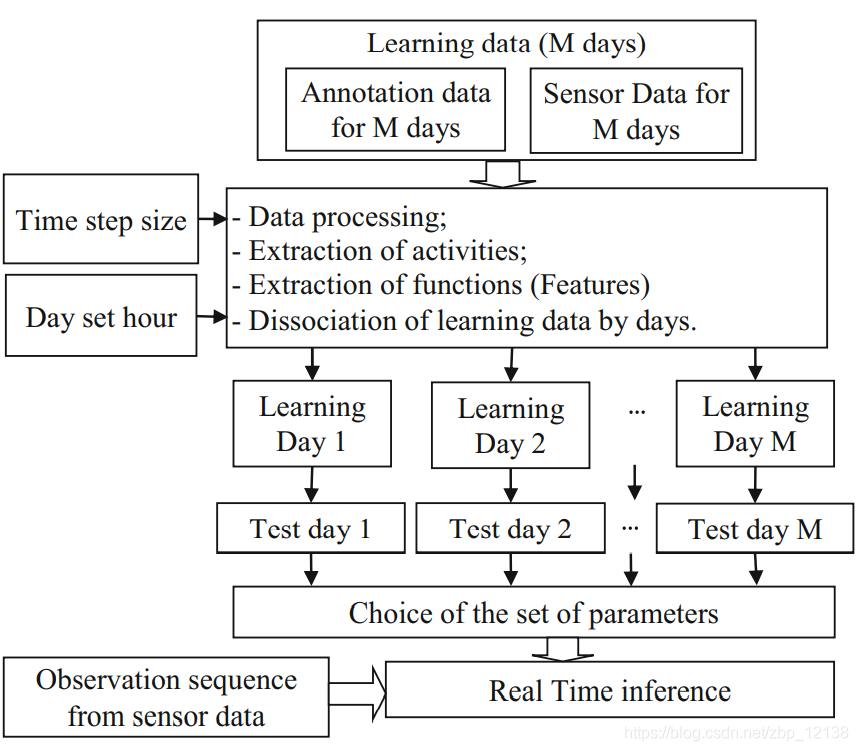
目前工作中采用的方法基于Kasteren等人在参考文献[29，31]中最初提出的方法。我们已经修改并开发了它，以便在LabVIEW环境下实现。选择LabVIEW环境是因为它以GUI的形式提供了高效的软件分析和用户友好的交互工具。在这些具体的发展和基于实验数据集的输入中，它可以提供各种简单的处理这些数据的可能性，为HMM参数的提取、验证以及应用于实时预测提供了各种可能性。因此，根据LabVIEW程序的要求，我们开发了一个虚拟仪器VI，它由两个主要部分组成，即方框图和GUI[3]。

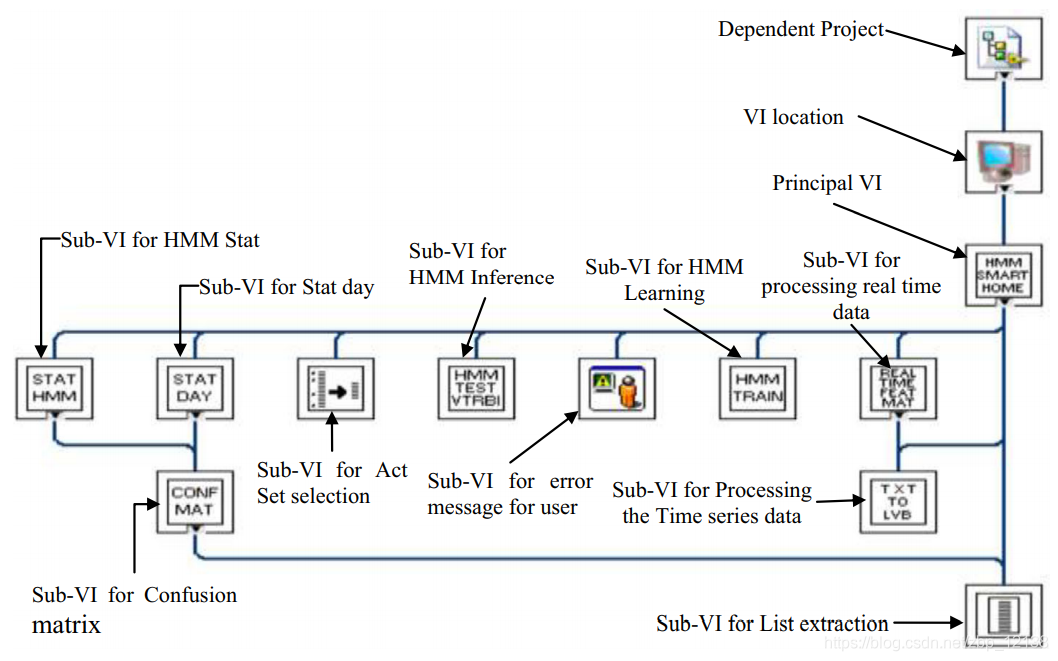
图2总结了应用程序的各个步骤。应该注意的是，这个应用程序的开发需要编程技术，在LabVIEW开发人员的社区中，这些技术被认为是高级编程技术。除了使用LabVIEW库中可用的一些函数外，还开发了专用于执行某些特定任务的子程序（sub-VIs），并将其添加到用户库中，如图3中主图的层次表示所示。这些专用VI和sub-VIs将在下面进行描述。

图2 说明整个建模过程的已实现GUI图的概要

图3 主程序的VI层次结构显示了主要开发的子VIs图标

2.1 实验数据的类型

该应用程序的实验学习数据输入有两种类型：人类日常家居活动的注释和安装在房屋不同位置的无处不在的传感器提供的数据。它们构成了两个按时间顺序排列的数据系列，并按照表1和表2中的两种格式记录在两个表中。

表1 人类活动的时序数据格式

表2 传感器活动时间数据格式

2.2 数据处理与离散化

在这一步中，从传感器获得的原始实验数据被离散为持续时间的时间片${\Delta }_t$[27，29]选择的时间足够长，可以区分，但足够短，可以提供高精度的标记结果。因此，在每个传感器处关联单个特征$x_t^i$，该特征$x_t^i$指示时间片$t$处的特征i的值为$x_t^i\in 0,1$。

特征值可以由直接从传感器获得的原始值来表示，也可以由Kasteren等人在参考文献中提出的变换来表示[29，31]，根据另外两种可能的表示过程之一：如图4所示的“最后激发”和“改变点”过程。

图4 使用原始值a上次激发、b最后激发、c变化点表示的传感器响应示例[29、31]

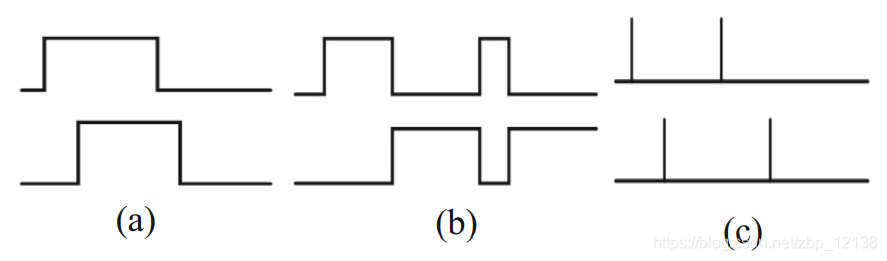
在“上次激发”程序中，上次激发的传感器，即最后给出值为1的传感器，在另一个传感器激发之前保持此值。在“变化点”程序中，当传感器的状态发生变化时，即从0变为1或从0变为1时，传感器将给出1；否则它保持在0。

在安装了N个传感器的房屋中，在一组$t$时间片上的时间片$t$处的观测值由以下向量表示：

$$\overrightarrow{x_t}={\left(x_t^1,x_t^2,\dots ,x_t^N\right)}^T(1)$$

并且时间片$t$的关联活动标签由$y_t$表示为$y_t\in \left\{\begin{array}{c}1，2，\dots ，Q\end{array}\right\}$表示$Q$可能的活动（HMM的状态）。

因此，在LabVIEW下的应用程序以及相应的GUI中，观测时间序列$X_{1:T}$将由维数为$N\cdot T$的二进制矩阵表示，用带有$T$个元素的数字向量来标记时间序列$Y_{1:T}$。在一定天数内观察到的这两组实验数据将被分离，以便将其子序列$X_{1:T^{\prime }}$（和$Y_{1:T^{\prime }}$）归属于每个实验日。这种分离是通过选择03:00作为一天开始的参考时间来完成的，因为在这个时间，标准家庭中的人类活动是最少的。

因此，对于每天，$d=1，2，3，\dots$，在一个由$D$天组成的观察小组中，对于每天时间序列中的项目数$T$，我们得到了观察时间序列：

$$X_{1:T^{\prime }}^d=\left({\vec{x}}_1,{\vec{x}}_2,\dots ,{\vec{x}}_{T^{\prime }}\right)（2）$$

以及相应的活动标签：

$$Y_{1:T^{\prime }}^d=\left(y_1,y_2,\dots ,y_{T^{\prime }}\right)（3）$$

最后，在总学习天数$D$上，我们将得到观测时间序列的一个维数为$D$的二元矩阵$X\times N\times T^{\prime }$和维数为$D$的活动标签时间序列矩阵$Y\times 1\times T^{\prime }$

应该注意的是，在这个阶段，如果考虑一个新的活动，当没有检测到对应于起始集的活动时，它将对应于归属于时间片的空闲活动。

2.3 隐马尔可夫模型

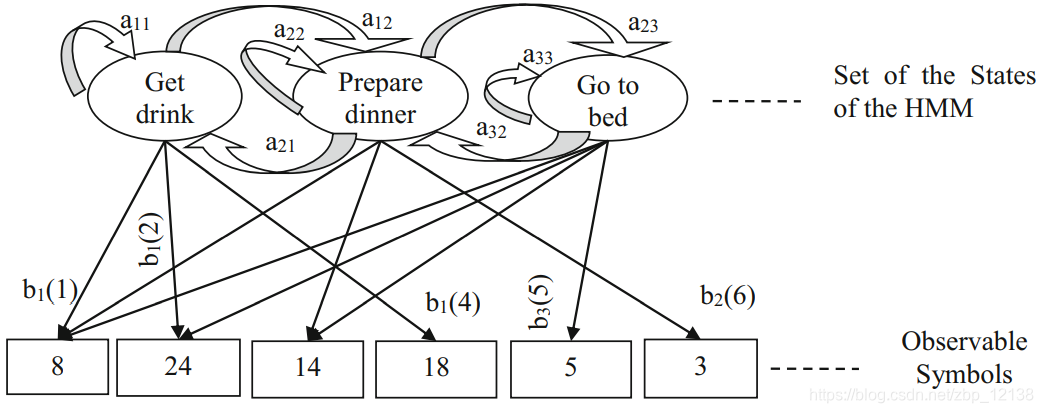
我们已经提到，允许在当前应用程序中开发的日常生活活动建模的交互式工具基于机器学习隐马尔可夫模型，HMM。HMM可以看作是Markov链的一个特例，Markov链是一个随机过程，它的转移由一个随机矩阵给出，它验证了Markov性质，即下一个状态只依赖于前一个状态。在隐马尔可夫模型中，状态是不可观察的（它们是隐藏的），但每个状态都可以随机地发射一组可见符号的元素之一[27]。因此存在一组隐藏状态和一组可观察符号。在当前应用中，隐藏变量对应于活动，可观察变量对应于传感器数据。根据Rabiner等人[22]提出的符号，图5给出了HMM的简单图形表示，突出显示了状态$(a_{ij})$和观察概率$(b_j(k))$之间的转移概率。

图5 在一个例子中给出了HMM的图形表示

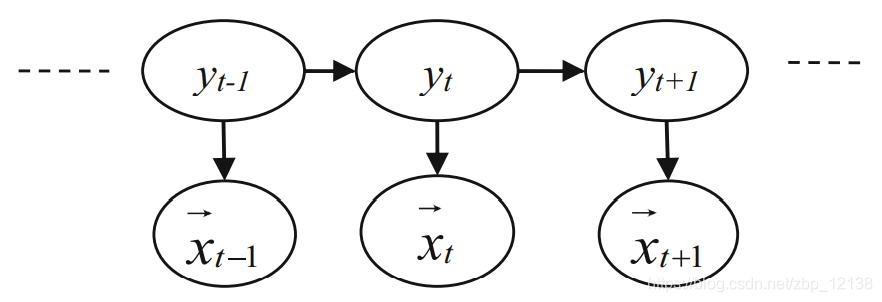
在上述变量的符号中，我们可以说模型的基本作用是在整个$T$时间片上建立观测序列$X_{1:T}$和活动标签序列$Y_{1:T}$之间的对应关系。我们在图6中报告了用于离散化数据的状态序列和观测序列之间互连的图形表示[29，31]。

图6 状态序列与HMM观测值之间的相互联系

为了有可能应用HMM，从而与主要的Markov性质相一致，在应用中必须考虑以下两个假设[22]：

• 时间片$t$处的活度$y_t$仅取决于时间片$t-1$处的活跃度$y_{t-1}$；
• 可观测变量$\overrightarrow{x_t}$，时间片$t$仅取决于此时片t的活动$y_t$

相应的联合概率分解如下：

$$p\left(y_{1:T},X_{1:T}\right)=p\left(y_1\right)\prod _{t=1}^{T}p\left(\overrightarrow{x_t}\mid y_t\right)\prod _{t=2}^{T}p\left(y_t\mid y_{t-1}\right)（4）$$

一个HMM及其参数被注意到$\Lambda =(A、B，B，\pi )$ 因此[7]：

• A = { a i j } A=\left\{a_{i j}\right\} A={aij​}是转移概率的矩阵，例如 $a_{ij}\equiv p\left(y_t=i\mid y_{t-1}=j\right)$;
• B = { b j ( k ) } B=\{b j(k)\} B={bj(k)}是观察概率的矩阵，例如 $b_j(k)\equiv p\left(\overrightarrow{x_t}=\overrightarrow{x_k}\mid y_t=j\right)$;
• And π = { π i } \pi=\left\{\pi_{i}\right\} π={πi​}是初始概率的向量，例如 ${\pi }_i\equiv p\left(y_1=i\right)$.

其中$i，j=1,2，\dots ，Q$（总活动次数）和$k=1,2，\dots ，k$（总观察次数）。

2.4 学习

众所周知，Baum-Welch算法是学习HMM参数的参考算法[22]。该方法的应用将需要$2^N$个参数来观察观察的分布，以考虑所有可能的组合，因此需要大量的学习元素，即使特征数量减少。因此，Kasteren等人[31]引入了另一种学习方法，其中每个特征独立于其他特征进行建模。在这种新方法中，每个活动有$N$个参数，每个特征由一个独立的Bernouli分布建模，其最大似然参数为${\mu }_{ni}$表示状态i的第$n$个特征。因此，转移分布由$Q$多项式分布来建模，每个活动一个，最后，初始概率向量遵循多项式定律。因此，模型参数为：

$$a_{ij}=\frac{{\sum }_{t=2}^T\delta \left(y_t,j\right)\delta \left(y_{t-1},i\right)}{{\sum }_{t=2}^T\delta \left(y_{t-1},i\right)}（5）$$

$${\mu }_{ni}=\frac{{\sum }_{t=1}^T{x}_t^n\delta \left(y_t,i\right)}{{\sum }_{t=1}^T\delta \left(y_t,i\right)}（6）$$

$${\pi }_i=\delta \left(y_1,i\right)（7）$$

其中，$\delta (i、j）$是Kronecker delta函数，如果$i=j$则为1，否则为0。

2.5 结论

其中一个主要的应用，其中HMMs是积极考虑是在解码或推理的问题，如在目前的工作。它包括找到模型的最佳状态序列，该序列会发出一个观察序列，即在我们的例子中，活动标签的最佳时间序列。这个序列对应于允许概率$P（Y1:T/X1:T）$最大化的序列。能够解决这个问题的算法是Viterbi算法，在参考文献中已经详细介绍了该算法[11, 22]。

在当前应用中，Viterbi算法在LabVIEW开发中作为子VI实现，该子VI在图2的框图中的“测试”和“实时推断”步骤中调用。

2.6 模型的性能评估

通过从混淆矩阵中提取四个性能指标来评价HMM的性能。这些是精度、召回率、F-度量和精确度，由以下等式定义[14、21、30]：

$$\text{ precision }=\frac{1}{Q}\sum _{i=1}^Q\frac{T{P}_i}{T{I}_i}（8）$$

$$\text{ recall }=\frac{1}{Q}\sum _{i=1}^Q\frac{T{P}_i}{T{T}_i}（9）$$

$$\text{ F-Mesure }=\frac{2\text{ precision.recall }}{\text{ precision }+\text{ recall }}（10）$$

$$\text{ accuracy }=\frac{{\sum }_{i=1}^{Q}T{P}_i}{\text{ Total }}（11）$$

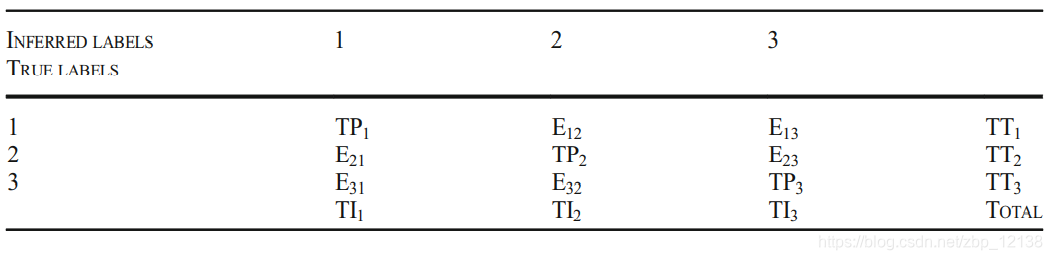
混淆矩阵的格式如表3所示，其中的行表示标签（活动）的真实值，列表示由模型推断出的值[14]。混淆矩阵是一种用来衡量机器学习模型性能的工具，它特别检查机器学习模型的预测与分类问题中的实际情况相比是否准确[25]。精确性指数提供了关于实际正确的阳性识别比例的信息[28]，召回指数与已正确识别的实际阳性结果的比例相关联[24]，F-Mesure指数是精确度和召回指数的加权平均值[4]，精确度是指模型预测与被建模现实匹配程度的度量[15]。因此，我们注意到，对于所有指标，结果的相关性为：真阳性TP、总真值TT、总推断TI和误差E。

表3 混淆矩阵格式

为了在当前应用中正确地开发和实现HMM方法，我们介绍了Tapia等人提出的方法“Leave-one-day”。该方法包括在整个日范围$D$中选择要推断的一个目的地日，并在所有$D$天中重复该序列。利用$D-1$天提供的实验数据，学习特定$D$天模型的参数。这一过程的结果是每个测试日的一组参数和一个观察序列矩阵。

先前定义的性能指标（方程式8~11）然后计算每个试验日的平均值及其标准偏差，从而对模型的性能进行全面评估。

三、图形用户界面

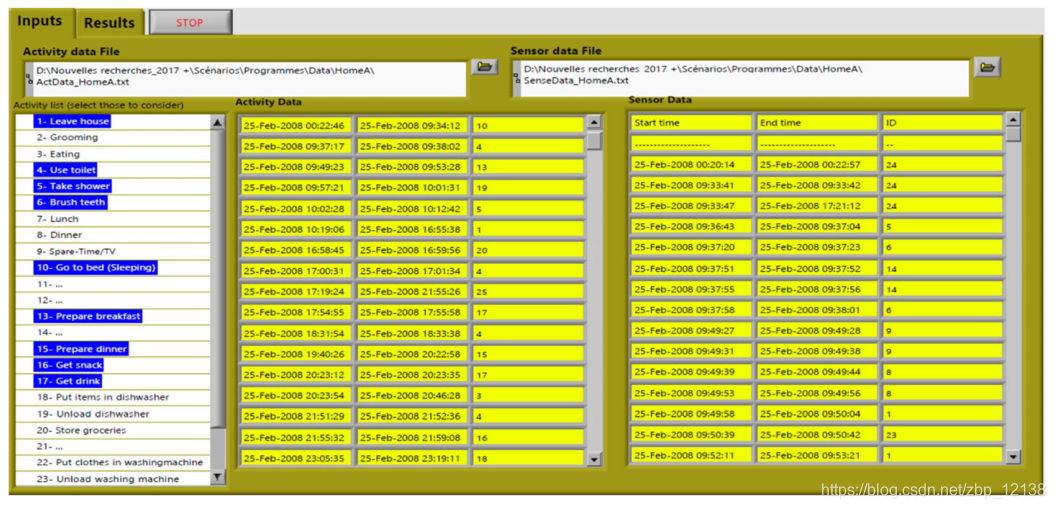
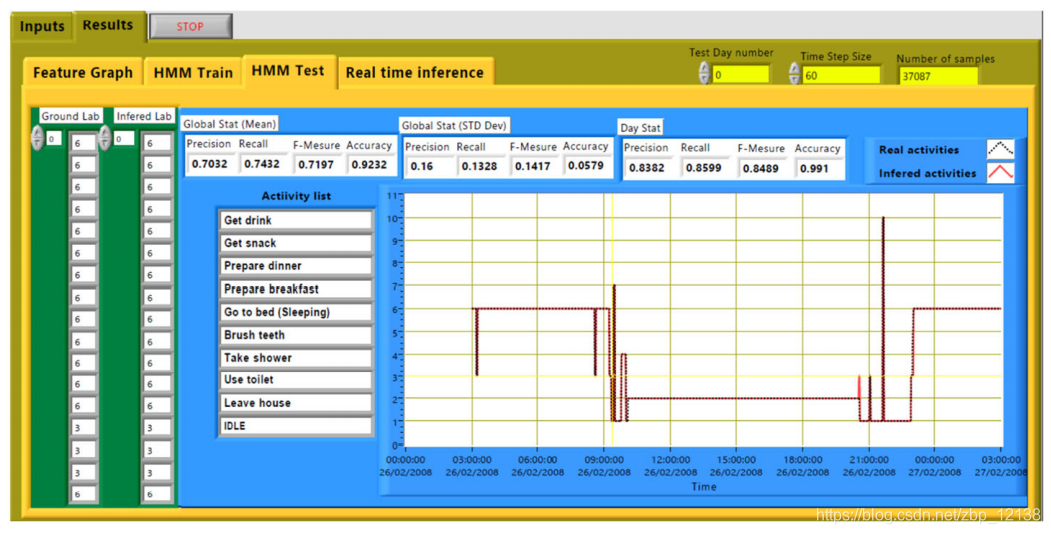
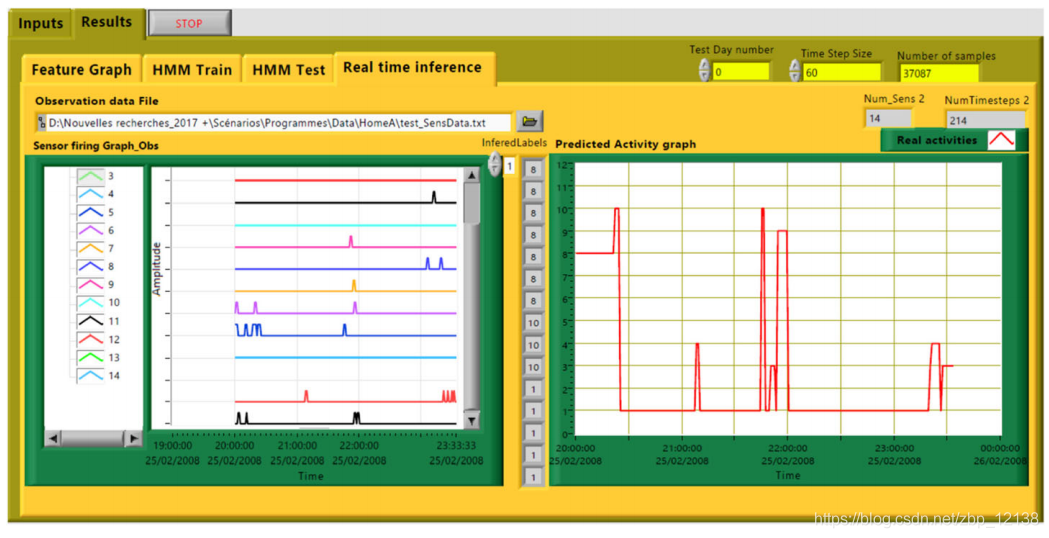
当前的人类日常生活活动识别应用程序的开发考虑到了LabVIEW通过GUI提供的用户友好的可能性，从而为最终用户提供了一个简单而方便的界面。在程序的启动阶段，显示交互式图形用户界面（GUI），并在整个过程中为用户隐藏完整的后台软件开发。图形用户界面由两个主页组成，可通过鼠标指针等指针设备直接激活。第一页与输入相关联。在这个页面中，用户通过上传测量文件和选择专用列表中的标签来输入实验学习数据。第二页与结果相关联。它专用于可视化测试日结果数据，必须通过增加专用按钮在整个$D$日范围内进行选择。以秒为单位的时间片长度（离散化时间）也将从专用控件中引入。第二页由四个子页组成。第一个子页面是“特征图”子页面，显示传感器触发活动（特征）随时间变化的叠加图。因此，每个图形对应于一个传感器，该传感器的值在触发时为1，其它为零。第二和第三个子页面是“HMM序列”和“HMM测试”子页面，分别显示参数和测试结果，以及实际活动和模型推断的活动之间的比较图。等式中定义的绩效指标。（方程式8~11）也显示在所选目的地测试日的“HMM测试”子页中。最后，子页面“HMM实时推断”被保留用于与可实时完成的传感器数据的另一观察序列相关联的活动序列的预测结果（传感器活动的瞬时读取）。

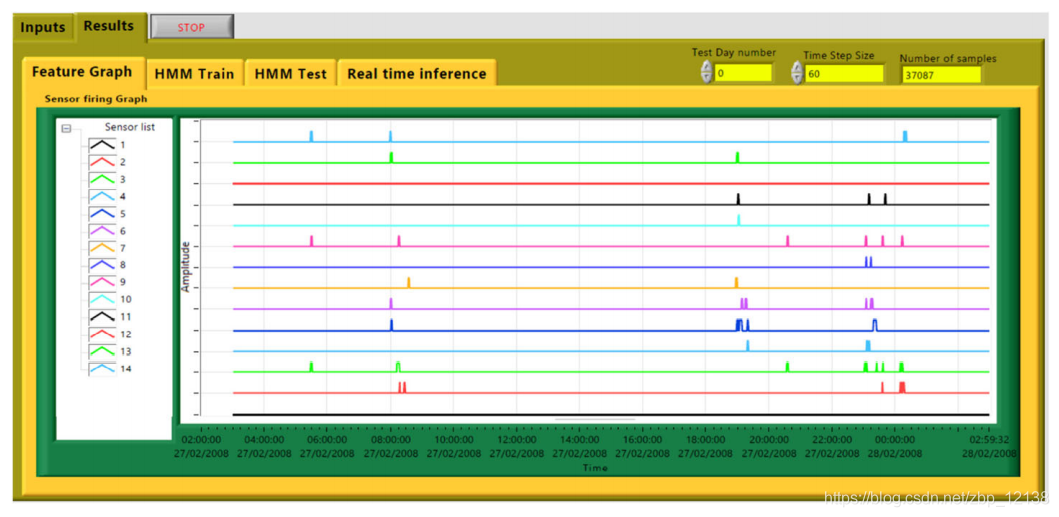
作为示例，在图中示出与特定日期的当前应用相关的对应页面（方程式7~11）。在图7中，“输入”页面包括参考房屋中存在的25次日常生活活动。在图8的子页“特征图”中，我们以Kasteren数据集中提出的第一个测试日获得的各种传感器的行为为例（注：如下所示，[31]中的Home A将对应于当前贡献中的homing-A），具有“ChangePoint”特征表示程序和1分钟的时间片长度。所考虑的传感器特性:1- 微波炉，2-卫生间门，3-卧室门，4-杯柜，5-冰箱，6-盘柜，7-前门，8-洗碗机，9-马桶冲水器，10-冰箱，11-锅柜，12-洗衣机，13-杂货柜，14-卧室门。图9中的“HMM序列”主要通过三个矩阵（A、B和B）的值来显示当天计算的HMM参数π). 图10中的“HMM测试”子页显示了实际活动和预测活动的图表，这些活动是时间的函数，带有测试日的性能指标以及所有学习日这些相同指标的平均值和标准差。最后，子页面“HMM实时推断”如图11所示，展示了从模型中推断出的预测结果。

图7 GUI的“输入”页面视图：实验数据的介绍和活动标签的选择

图8 GUI“功能图”子页的视图示例（传感器功能标签见文本中的注释）

图9 GUI“结果”页的“HMM Train”子页的视图

四、验证和讨论

在上面的例子中，开发的工具已经被应用于验证在文献中发现的几组实验数据。特别是，我们将我们的模型应用于Van Kasteren等人[31]提供的输入数据系列，这些数据系列记录在作者命名的房子“Home A”中，并由Ord提供óñez等人[21]，关于第二个由作者命名的“Set A”。这两个系列的数据在当前的贡献中分别被命名为住宅A和住宅B。

如上所述使用“leave-one-day”方法，通过HMM模型推断出每个测试日的活动，HMM模型的参数集由所选面板的其他研究日提供的实验数据学习。将每个推断的活动序列与相应测试日的实际活动序列进行比较。结果可以显示在子页面“HMM测试”中，如图10所示。

图10 GUI“结果”页的“HMM测试”子页的视图

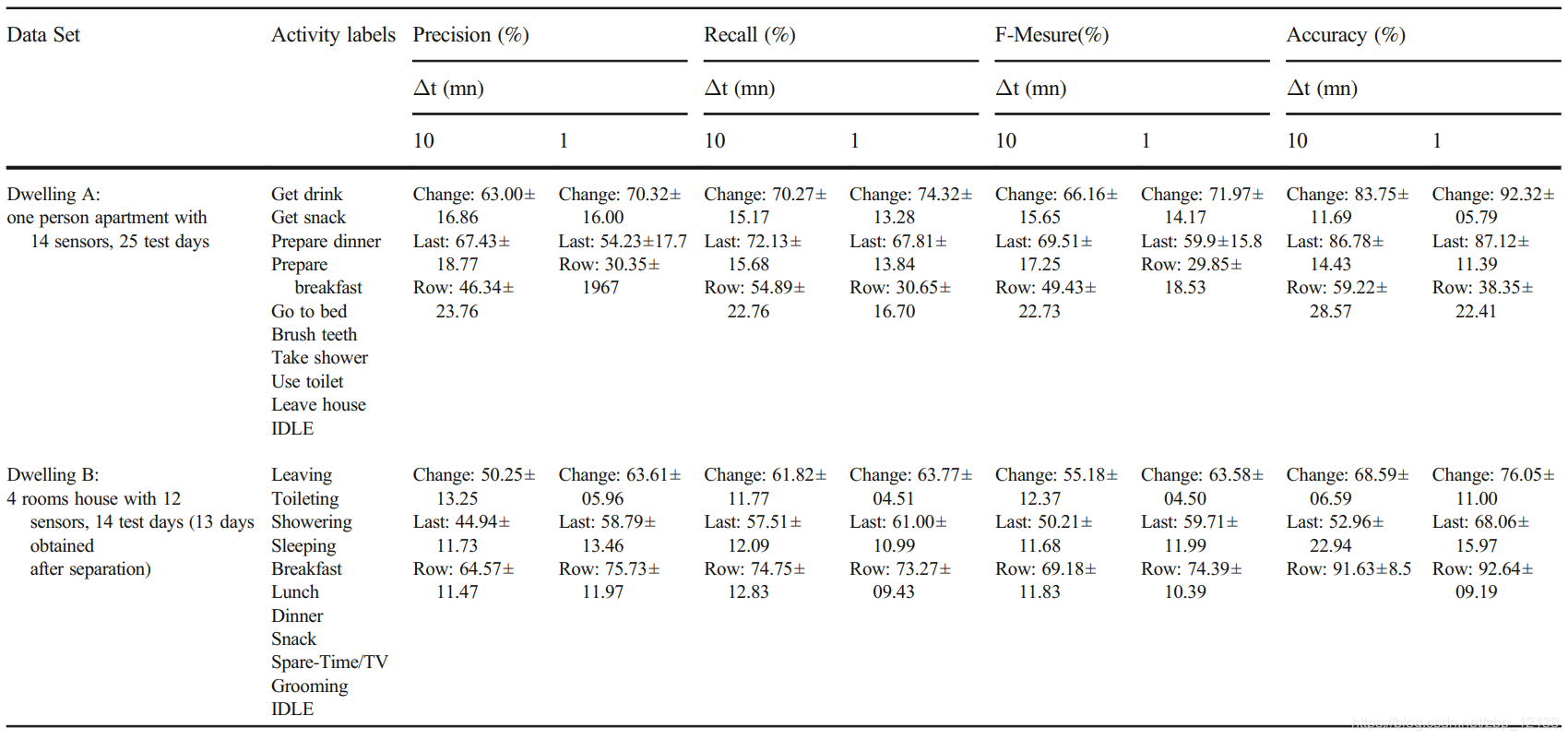
因此，我们观察了特征表示的三个过程中的每一个的“leave-one-day”结果，即，作为提醒，最后激发和变更点对于两个离散化时间长度$(\Delta t）$ ，分别等于10分钟和1分钟。表4列出了两个住宅所有测量日的平均值和标准差。

表4 两个研究案例的绩效结果（精确性、召回率、F-Measure和准确度）

乍一看，我们注意到实现的模型对于两组实验数据的行为是不同的。这种差异归因于两组性能指标中的一组和另一组的值之间的离散度。

从表4中可以看出，“最后一次激发”特征转换过程，当住宅A数据集的时间步长为10min时，模型给出了更好的推理结果（86.78%± 14.43%准确率，72.13%± 15.68%召回率，67.43%±18.77%精确度）。相反，对于一分钟的时间步长，使用相同的数据集，“变化点”程序将确保更好的模型推断，从而提供更高的性能指标值（92.32%± 5.79%准确率，70.32%±16%精确度）。然而，对于住宅B数据集，“Row”程序在两个时间步长内提供了更好的模型推断，在一分钟内具有更高的性能（92.64%±9.19% 准确率，73.27%± 9.43%召回率，75.73%± 11.97%精确度）。因此，可以首先总结分析的第一部分的一些基本原理。事实上，我们清楚地看到，得到的结果指出了离散化时间步长长度的巨大影响$(\Delta t）$ 以及转换程序的不等价性。但是，我们不能根据性能来明确地对过程进行分类，因为这些过程直接与数据集本身相联系。我们将这两个数据集所得结果之间的差异归因于学习天数、所考虑的活动数量和传感器数量的影响。

然而，有了这个新的用户友好的工具，可以以一种简单的方式获得精确性、召回率、F-测量值和准确性的实际结果，使用该分析结果的用户或应用程序将能够访问这三种表示，从而提供了手动或自动的可能性，使用最好的独立于数据集和实现最高精度的隐马尔可夫模型。此外，我们的结果与作者最初用原始实验数据获得的结果非常接近，如Van Kasteren等人[31]用Matlab开发的方法进行分析的情况。

因此，该工具可以作为一个功能性的，甚至工业和商业产品使用，因此在智能家居能源管理系统的未来项目中被认为是一个黑匣子。对于一个完整的研究能源消耗的家庭，居民或能源经理只需输入实验数据记录在几天。然后，根据活动标签的相对负荷，考虑其电力需求，用户将获得作为输出的每个测试日对应的负荷曲线和能耗预测。对于特定的实时预测，他可以选择一组参数作为输入。实际上，对于后者，应用程序为他提供了可能性，从子页面“实时推断”（参见：图11）验证HMM的参数集并开始预测。

图11 GUI“结果”页的“实时推断”子页的视图

五、总结

目前的手稿概述了一个原始的和交互式的图形工具，允许建模，测试和用户友好的智能家居日常生活活动预测的发展。此工具是在LabVIEW下开发的。应用程序的输入是两个时间序列数据，这些数据来自于一个无处不在的传感器网络，用于特征和活动标签的注释。该方法基于隐马尔可夫模型，具有时间建模能力。实验结果显示在图形用户界面使用LabVIEW。从文献提供的真实输入数据得到的结果与类似研究的结果更接近。在我们的应用验证中，它证明了所选择的方法的有效性，例如与目前在识别过程中使用的纯序贯方法相比较。

从验证结果来看，我们注意到特征表示过程的选择取决于实验本身，因此需要对一组实验数据应用三个过程，即Row、Last fired和ChangePoint过程，以便能够为每个数据集选择合适的过程。

该工具的一个独到之处是在LabVIEW环境下进行了开发，通过图形用户界面为用户提供了交互性和友好性。所获得的结果与交互式图形工具相关联，证明了将这些工具集成到智能家居中的可能性，以便根据在所考虑的环境中离线记录的人类活动的实验数据集，预测或管理作为人类活动函数的能源消耗。此外，在LabVIEW下的开发为实时监控打开了大门，集成了实时传感器数据采集模块。除了对未来工作的这种观点，以及基于所实现的模型提供的判别可能性，考虑非二进制传感器允许在智能家居中预测真实的人类活动的能量消耗更大的可靠性将是有价值的。

参考文献

1. Alaa M, Zaidan AA, Zaidan BB, Talal M, Kiah MLM (2017) A review of smart home applications based on
   internet of things. J Netw Comput Appl 97:48–65. https://doi.org/10.1016/j.jnca.2017.08.017
2. Aldrich FK (2006) Smart homes: past, present and future. Insid Smart Home:17–39. https://doi.org/10.
   1007/1-85233-854-7_2
3. Bitter R, Mohiuddin T, Nawrocki M (2007) LabView advanced programming techniques. CRC Press
4. Brank J, Mladenić D, Grobelnik M, Liu H, Mladenić D, Flach PA, Garriga GC, Toivonen H, Toivonen H
   (2011) F-measure. In: Sammut C, Webb GI (eds) Encyclopedia of machine learning. Springer, Boston, pp
   416–416. https://doi.org/10.1007/978-0-387-30164-8_315
5. Brecha RJ, Mitchell A, Hallinan K, Kissock K (2011) Prioritizing investment in residential energy
   efficiency and renewable energy — A case study for the U. S. Midwest. Energy Policy 39(5):2982–
6. https://doi.org/10.1016/j.enpol.2011.03.011
7. Chernbumroong S, Cang S, Atkins A, Hongnian Y (2013) Elderly activities recognition and classification
   for applications in assisted living. Expert Syst Appl 40(5):1662–1674. https://doi.org/10.1016/j.eswa.2012.
   09.004
8. Cornuéjols A, Miclet L (2002) Apprentissage Artificiel Concepts et Algorithmes. EYROLLES
9. Ferrández-Pastor FJ, Mora-Mora H, Sánchez-Romero JL, Nieto-Hidalgo M, García-Chamizo JM (2017)
   Interpreting human activity from electrical consumption data using reconfigurable hardware and hidden
   Markov models. J Ambient Intell Humaniz Comput 8(4):469–483. https://doi.org/10.1007/s12652-016-
   0431-y
10. Fleury A, Vacher M, Noury N (2010) SVM-based multimodal classification of activities of daily living in
    health smart homes: sensors, algorithms, and first experimental results. IEEE Trans Inf Technol Biomed 14:
    274–283. https://doi.org/10.1109/TITB.2009.2037317
11. Geller H, Schaeffer R, Szklo A, Tolmasquim M (2004) Policies for advancing energy efficiency and
    renewable energy use in Brazil. Energy Policy 32(12):1437–1450. https://doi.org/10.1016/S0301-4215(03)
    00122-8
    Multimedia Tools and Applications11. Grewal JK, Krzywinski M, Altman N (2019) Markov Models — Hidden Markov Models. Nat Methods
    16(9):795–796. https://doi.org/10.1038/s41592-019-0532-6
12. Hellgren M (2015) Energy Use as a Consequence of Everyday Life. https://doi.org/10.3384/diss.diva122253
13. Hu Q, Li F (2013) Hardware Design of Smart Home Energy Management System with dynamic Price
    response. IEEE Trans Smart Grid 4(4):1878–1887. https://doi.org/10.1109/TSG.2013.2258181
14. Japkowicz N (2006) “Why question machine learning evaluation methods? (An illustrative review of the
    shortcomings of current methods).” AAAI-2006 Workshop on Evaluation Methods for Machine Learning,
    6
15. Kakas AC, Cohn D, Dasgupta S, Barto AG, Carpenter GA, Grossberg S, Webb GI et al (2011) Accuracy.
    In: Sammut C, Webb GI (eds) Encyclopedia of machine learning. Springer, Boston, pp 9–10. https://doi.
    org/10.1007/978-0-387-30164-8_3
16. Kang J, Kim M, Park JH (2016) A reliable TTP-based infrastructure with low sensor resource consumption
    for the smart home multi-platform. Sensors (Switzerland) 16(7):1–15. https://doi.org/10.3390/s16071036
17. Karaman S, Benois-Pineau J, Dovgalecs V, Mégret R, Pinquier J, André-Obrecht R, Gaëstel Y, Dartigues
    JF (2014) Hierarchical hidden Markov model in detecting activities of daily living in wearable videos for
    studies of dementia. Multimed Tools Appl 69(3):743–771. https://doi.org/10.1007/s11042-012-1117-x
18. Kim MJ, Myoung Won O, Cho ME, Lee H, Kim JT (2013) A critical review of user studies on healthy
    smart homes. Indoor Built Environ 22(1):260–270. https://doi.org/10.1177/1420326X12469733
19. Li Y, Peng X, Zhou G, Zhao H (2020) SmartJump: a continuous jump detection framework on
    smartphones. IEEE Internet Comput 24(2):18–26. https://doi.org/10.1109/MIC.2020.2969610
20. Liouane Z, Lemlouma T, Roose P, Weis F, Messaoud H (2016) A Markovian-based approach for daily
    living activities recognition. In: SENSORNETS 2016 - Proceedings of the 5th International Confererence
    on Sensor Networks, 214–19. https://doi.org/10.5220/0005809502140219.
21. Ordóñez J, de Toledo FP, Sanchis A (2013) Activity recognition using hybrid generative/discriminative
    models on home environments using binary sensors. Sensors (Switzerland) 13(5):5460–5477. https://doi.
    org/10.3390/s130505460
22. Rabiner LR, Juang BH (1986) An introduction to hidden Markov models. IEEE ASSP Mag 3(1):4–16.
    https://doi.org/10.1109/MASSP.1986.1165342
23. Ricquebourg V, Menga D, Durand D, Marhic B, Delahoche L, Logé C (2006) The smart home concept: our
    immediate future. 2006 1st IEEE International Conference on E-Learning in Industrial Electronics, ICELIE,
    no. May 2014: 23–28. https://doi.org/10.1109/ICELIE.2006.347206
24. Sammut C, Webb GI, eds. (2010) Recall. In: Encyclopedia of Machine Learning, 829. Boston: Springer.
    https://doi.org/10.1007/978-0-387-30164-8_702
25. Shultz TR, Fahlman SE, Craw S, Andritsos P, Tsaparas P, Silva R, Drummond C, Ling CX, Sheng VS,
    Drummond C, Lanzi PL, Gama J, Wiegand RP, Sen P, Namata G, Bilgic M, Getoor L, He J, Jain S, Stephan
    F, Jain S, Stephan F, Sammut C, Harries M, Sammut C, Ting KM, Pfahringer B, Case J, Jain S, Wagstaff
    KL, Nijssen S, Wirth A, Ling CX, Sheng VS, Zhang X, Sammut C, Cancedda N, Renders J-M, Michelucci
    P, Oblinger D, Keogh E, Mueen A (2011) Confusion matrix. In: Sammut C, Webb GI (eds) Encyclopedia of
    machine learning. Springer, Boston, pp 209–209. https://doi.org/10.1007/978-0-387-30164-8_157
26. Tahir SF, Fahad LG, Kifayat K (2019) Key feature identification for recognition of activities performed by a
    smart-home resident. J Ambient Intell Humaniz Comput 11:2105–2115. https://doi.org/10.1007/s12652-
    019-01236-y
27. Tapia EM, Intille SS, Larson K (2004) Activity recognition in the home using simple and ubiquitous
    sensors. Lect Notes Comput Sci 3001:158–175. https://doi.org/10.1007/978-3-540-24646-6_10
28. Ting KM (2010) Precision. In: Sammut C, Webb GI (eds) Encyclopedia of Machine Learning, vol 780.
    Springer, Boston. https://doi.org/10.1007/978-0-387-30164-8_651
29. van Kasteren T, Noulas A, Englebienne G, Kröse v (2008) “Accurate activity recognition in a home
    setting.” UbiComp 2008 - proceedings of the 10th international conference on ubiquitous computing, 2008.
    https://doi.org/10.1145/1409635.1409637.
30. van Kasteren TML, Englebienne G, Kröse B (2010) Activity recognition using semi-Markov models on real
    world smart home data sets. J Ambient Intell Smart Environ 2:311–325
31. Van Kasteren TLM, Englebienne G, Kröse BJA (2011) Human activity recognition from wireless sensor
    network data: benchmark and software. Act Recognit Pervasive Intell Environ 4:165–186. https://doi.org/
    10.2991/978-94-91216-05-3_8
    Multimedia Tools and Applications32. Weber S, Puddu S, Pacheco D (2017) Move it! How an electric contest motivates households to shift their
    load profile. Energy Econ 68:255–270. https://doi.org/10.1016/j.eneco.2017.10.010
32. Zhou B, Li W, Chan KW, Cao Y, Kuang Y, Liu X, Wang X (2016) Smart home energy management
    systems: concept, configurations, and scheduling strategies. Renew Sust Energ Rev 61:30–40. https://doi.
    org/10.1016/j.rser.2016.03.047
33. Zipperer A, Aloise-Young PA, Suryanarayanan S, Roche R, Earle L, Christensen D, Bauleo P, Zimmerle D
    (2013) Electric energy Management in the Smart Home: perspectives on enabling technologies and
    consumer behavior. Proc IEEE 101(11):2397–2408. https://doi.org/10.1109/JPROC.2013.2270172

译文作者简介

• 北京联合大学 机器人学院 自动化专业 2018级 本科生 郑博培
• 中国科学院自动化研究所复杂系统与智能科学实验室实习生
• 百度飞桨开发者技术专家 PPDE
• 百度飞桨官方帮帮团、答疑团成员
• 深圳柴火创客空间 认证会员
• 百度大脑 智能对话训练师
• 阿里云人工智能、DevOps助理工程师