滴滴定价策略算法

一、Boosting 与 Bagging 的区别

特性	Bagging	Boosting
核心思想	并行训练多个弱模型，投票或平均输出结果	顺序训练多个弱模型，前一个模型的错误由后一个模型纠正
训练方式	并行	串行
数据采样	对训练集进行有放回采样（Bootstrap）	每轮根据前一轮模型的错误样本加权采样
模型权重	所有弱模型权重相等	弱模型按性能分配权重
减少偏差/方差	主要减少方差	主要减少偏差
抗过拟合能力	强（尤其是随机森林）	弱，容易过拟合（需调参）
常见算法	随机森林（Random Forest）	AdaBoost, Gradient Boosting, XGBoost
对异常值敏感性	不敏感	敏感
适用场景	数据噪声大或复杂度高的场景	强调准确率、希望降低偏差的任务

• Bagging：强调“减少方差”，适合模型不稳定的场景。
• Boosting：强调“减少偏差”，适合模型偏差较大的情况。

二、梯度下降与梯度提升的区别

2.1. 梯度下降的更新公式（在参数空间）

梯度下降是通过最小化损失函数，来更新模型参数：

公式：

对于参数 $\theta$，损失函数 $L(\theta )$，学习率 $\eta$，每一步更新为：
$${\theta }_{t+1}={\theta }_t-\eta \cdot {\nabla }_{\theta }L({\theta }_t)$$

• 目标：通过不断迭代优化参数，使损失函数最小。
• 空间：在参数空间中进行优化。

2.2. 梯度提升（Gradient Boosting）

梯度提升是一种 Boosting 方法，不直接优化参数，而是每一轮在函数空间中向负梯度方向逼近损失最小的函数。

思路：

• 假设我们要学习一个模型 $F(x)$，使得损失函数 $L(y,F(x))$ 最小；
• 每一轮构建一个新的弱模型 $h_t(x)$，使其逼近当前损失函数关于模型输出的负梯度：
  $$h_t(x)\approx -\frac{\partial L(y,F_{t-1}(x))}{\partial F_{t-1}(x)}$$
• 然后更新模型：
  $$F_t(x)=F_{t-1}(x)+\eta \cdot h_t(x)$$
• 目标：不断在函数空间中逼近最优模型。
• 空间：在函数空间中进行优化。

2.3. 梯度下降 vs 梯度提升

项目	梯度下降（Gradient Descent）	梯度提升（Gradient Boosting）
优化对象	模型参数 $\theta$	函数 $F(x)$
所在空间	参数空间	函数空间
迭代方向	参数的负梯度方向	当前损失对模型输出的负梯度方向
每轮优化方式	数值更新参数	拟合残差（负梯度）
最终模型结构	单一模型参数	多个弱模型累加成的复合模型
应用领域	线性回归、神经网络等	决策树提升（如 XGBoost、LightGBM）

2.4. 总结

• 梯度下降是在给定模型结构下优化参数；
• 梯度提升是在函数空间中逐步构建一个更好的函数逼近器；
• 两者都利用“梯度”的概念，但优化的对象和空间不同。

三、XGBoost 与 GBDT 的区别

3.1. 基本概念

• GBDT（Gradient Boosting Decision Tree）：基于梯度提升思想，每一轮训练一个决策树来拟合上一轮模型的残差（一阶梯度）。
• XGBoost（Extreme Gradient Boosting）：对传统 GBDT 在多个方面进行改进和优化，提升训练效率和泛化能力。

3.2. 核心区别

项目	GBDT	XGBoost
使用的梯度信息	一阶梯度	一阶 + 二阶梯度（泰勒二阶展开）

XGBoost 将损失函数做二阶泰勒展开：
$$L^{(t)}=\sum _i[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t(x_i{)}^2]+\Omega (f_t)$$

3.3. 分裂节点选择策略

• GBDT：遍历所有特征的所有可能切分点，计算分裂后残差的平方和（Gain）。
• XGBoost：利用 贪心算法 在特征维度上寻找最大增益的分裂点，增益计算基于一阶与二阶梯度：
  $$\text{Gain}=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma$$

3.4. 工程优化（加速训练）

优化点	描述
列块存储	使用按列存储的方式，方便快速遍历特征
缓存优化	预存分裂点直方图，加速计算
Sparsity-aware	对缺失值和稀疏输入自动处理
支持并行特征分裂搜索	特征维度级别并行化，而非树结构并行（GBDT不具备）
支持分布式训练	内建分布式能力，可在多机上训练

• 列块存储结构：通过将数据存储在内存中并按特征值排序，优化了分裂点查找的效率。
• 缓存感知访问：通过预取（prefetching）技术减少了缓存未命中（cache miss）的开销。
• 外核计算：通过将数据分块存储到磁盘上，并在需要时预取到内存中，使得系统能够处理超出内存容量的数据。
• 稀疏数据支持：通过在树节点中引入默认方向，XGBoost能够高效处理稀疏数据。

四、104. 二叉树的最大深度

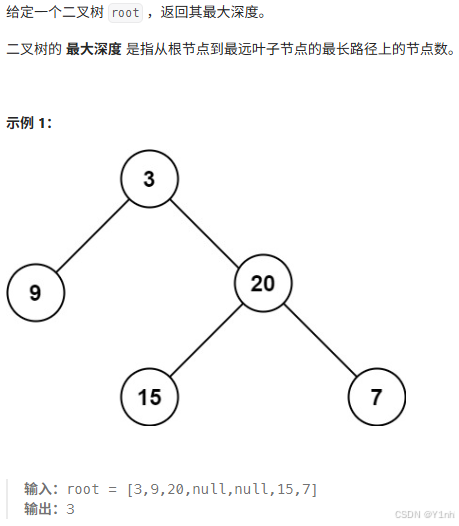
• 代码

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        l_depth = self.maxDepth(root.left)
        r_depth = self.maxDepth(root.right)
        return max(l_depth, r_depth) + 1

五、46. 全排列

• 代码：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        ans = []
        path = [0] * n     # 所有排列的长度都是一样的 n
        def dfs (i, s):    # 从答案的角度，第i个位置该从s中选择哪一个。
            if i==n:
                ans.append(path.copy())
                return
            for x in s:
                path[i] = x
                dfs(i+1,  s-{x})
        dfs(0, set(nums))
        return ans