统计学习方法——感知机

什么是感知机

参考用书是统计学习方法（李航）

感知机是一个二分类线性判别模型，假设输入$x\in {\mathbb{R}}^n$，输出$y\in -1,+1$，感知机为如下函数：
$$\begin{gathered} f(x)=sign(w^{T}x+b), \\ sign(z)=\{\begin{array}{ll}1& z\ge 0\\ -1& z<0\end{array} \end{gathered}$$
其中，w叫做权重，是分类超平面的法向量；b叫做偏置，是超平面的截距。

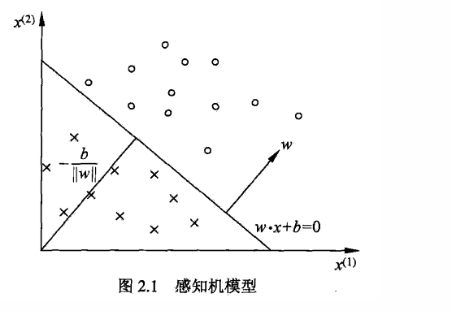
$x$和$w$都是向量，比如在上面的图2.1中，$x$就是2维的，因为数据平面的横轴和竖轴分别是$x^{(1)}$和$x^{(2)}$，感知机本质上是给每个特征加个权重$w$和偏置$b$从而进行分类的，因此如果数据落在超平面上，则$w^{T}x+b$就为0，落上超平面的上方则大于0，下方小于0。

设数据集线性可分，感知机的损失函数为所有误分类点到分类超平面的函数间隔，即：
$$L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$
下面简单解释下什么是函数间隔和几何间隔

函数间隔

函数间隔通常表示为:$|w\cdot x_1+b|$

其中$w$和$x_1$都是n维的向量，$x_1$为第一组样本的数据向量，这个式子表示的就是$x_1$这个数据点到超平面$w\cdot x+b=0$的距离。但是函数间隔会带来一个问题，计算机在优化的时候，会同时缩小$w$和$b$的值来减小$|w\cdot x_1+b|$

假设 $|w\cdot x_1+b|=1000$，如果去优化这个式子，计算机很有可能同时缩小$w$和$b$变成 $|\frac{1}{1000}w\cdot x_1+\frac{1}{1000}b|=1$，但是这样肯定是不行的，因为w的值本质上是没有变化的只是等比例缩小了。所以就需要几何间隔。

几何间隔

几何间隔通常表示为:$\frac{1}{||w||}|w\cdot x_1+b|$

就是在函数间隔中加入了$w$的$L_2$范数

$L_2$范数定义为$||w|{|}_2=\sqrt{{\sum }_{i=1}^N{w}_i^2}$

因此当出现$w$和$b$同时缩小1000倍的情况时，

$\frac{1}{||w||}|\frac{1}{1000}w\cdot x_1+\frac{1}{1000}b|$， 其中$||w||$为$\frac{1}{1000}\sqrt{{\sum }_{i=1}^N{w}_i^2}$，取个倒数就能将公式里面的$\frac{1}{1000}$化掉。

结果变为$\frac{1}{\sqrt{{\sum }_{i=1}^N{w}_i^2}}|w\cdot x_1+b|$。此时w向量的值就能被优化了。

• 为什么感知机不使用几何间隔

  由于感知机的前提是原数据集线性可分，这意味着必须存在一个正确的超平面。那么，不管几何距离还是函数距离，损失函数最后都要等于0，因此感知机并不关心点到超平面之间的间隔，关心的是误分类的点的个数。采用几何间隔其实也可以，但是会使学习过程复杂化。

感知机的原始形式

给定一个训练的数据集$T=(x_1,y_1),(x_2,y_2),..,(x_N,y_N)$，其中$x_i\in {\mathbb{R}}^n$，$Y_i\in -1,1$，$ i= 1,2,3…N$。感知机 $sign(w\cdot x+b)$ 的损失函数为:
$$\underset{w,b}{\min }L(w,b)=-\sum _{x_i\in M}{y}_i(w\cdot x_i+b)$$
其中M为误分类点的集合，有了损失函数分别对w和b求偏导就可以得到梯度了，损失函数$L(w,b)$的梯度为：
$$\begin{gathered} {\nabla }_{w}L(w,b)=-\sum _{x_i\in M}{y}_i{x}_i \\ {\nabla }_{b}L(w,b)=-\sum _{x_i\in M}{y}_i \end{gathered}$$
接着就可以随机选取一个失误分类$(x_i,y_i)$，对w,b进行更新:
$$\begin{gathered} w\leftarrow w+\eta y_i{x}_i \\ b\leftarrow b+\eta y_i \end{gathered}$$

其中$\eta (0<\eta \le 1)$是步长，又称为学习率，在本文中如果不做详细说明一般取1

可以得到如下的算法了:

输入：训练数据$T=(x_1,y_1),(x_2,y_2),..,(x_N,y_N)$，其中$x_i\in {\mathbb{R}}^n$，$Y_i\in -1,1$；学习率$\eta \in (0,1]$

输出：w,b；感知机模型$f(x)=sign(w^{T}x+b)$

• 随机任选一个超平面$w_0,b_0$，一般都初始化为0

• 在训练集中选取数据$(x_i,y_i)$

• 如果$y_i(w^T{x}_i+b)\le 0$，则更新w和b：

  ​ $$\begin{gathered} w=w+\eta y_i{x}_i \\ b=b+\eta y_i \end{gathered}$$

• 转至第二步，直到训练集中没有误分点

这个算法的流程简单来说就是：刚开始初始化超平面为0，然后选取第一个数据，如果结果小于等于0的话，那么就更新w和b，然后用更新后的新模型再次遍历所有数据，碰到错误情况就重复：更新w和b，遍历所有数据这个操作。直到找到合适的w和b满足所有的数据。

具体的例子可看统计学习方法（李航）第29页

感知机的对偶性质

对偶性这里直接贴出知乎上的一篇回答，写的非常好（https://www.zhihu.com/question/26526858）

这个回答和李航书中讲的角度不一样，但是解释的非常好！而且训练过程也有不同的地方，因为没有用${\alpha }_i$ ，因为这个回答的所有操作都是对$n_i$进行的，在更新时，是将$n_i+1$，这个公式和书中的${\alpha }_i={\alpha }_i+\eta$本质是一样的。

因为${\alpha }_i=n_i\eta$，所以${\alpha }_i=（n_i+1）\eta =n_i\eta +\eta ={\alpha }_i+\eta$