58、使用PCA进行数据降维和可视化【用Python进行AI数据分析进阶教程】
摘要:本文介绍了主成分分析(PCA)作为一种无监督的线性降维技术,其核心思想是通过线性变换将原始数据转换为一组各维度线性无关的主成分,按方差从大到小排列,以保留数据的主要信息。文中强调了PCA的关键点包括方差最大化、正交性和降维功能,并指出了在实际应用中需要注意的数据标准化、主成分解释难度以及维度选择问题。同时,文章提供了一个基于Python和scikit-learn库的示例,演示了如何对鸢尾花数
用Python进行AI数据分析进阶教程58:
使用PCA进行数据降维和可视化
关键词:主成分分析、数据降维、方差最大化、正交性、数据可视化
摘要:本文介绍了主成分分析(PCA)作为一种无监督的线性降维技术,其核心思想是通过线性变换将原始数据转换为一组各维度线性无关的主成分,按方差从大到小排列,以保留数据的主要信息。文中强调了PCA的关键点包括方差最大化、正交性和降维功能,并指出了在实际应用中需要注意的数据标准化、主成分解释难度以及维度选择问题。同时,文章提供了一个基于Python和scikit-learn库的示例,演示了如何对鸢尾花数据集进行PCA降维并可视化结果,展示了PCA在数据处理中的具体应用方式及其优势。
👉 欢迎订阅🔗
《用Python进行AI数据分析进阶教程》专栏
《AI大模型应用实践进阶教程》专栏
《Python编程知识集锦》专栏
《字节跳动旗下AI制作抖音视频》专栏
《智能辅助驾驶》专栏
《工具软件及IT技术集锦》专栏
一、原理概述
主成分分析(PCA)是一种无监督的线性降维技术,用于在减少数据集维度的同时保留尽可能多的信息。其核心思想是通过线性变换将原始数据转换为一组各维度线性无关的主成分,这些主成分按方差从大到小排列,方差越大包含的信息越多。
二、关键点
- 方差最大化:PCA 旨在找到能使数据投影后方差最大的方向,这样能保留数据的主要信息。
- 正交性:主成分之间相互正交,即它们之间不存在线性相关性,避免了信息冗余。
- 降维:通过选择前 k 个主成分(k<p,p 为原始特征数量),将数据从高维空间映射到低维空间。
三、注意点
- 数据标准化:PCA 对数据尺度敏感,不同特征的尺度差异可能导致某些特征在分析中占据主导地位。因此,在进行 PCA 之前,通常需要对数据进行标准化处理,使各特征具有相同的尺度。
- 主成分解释:主成分是原始特征的线性组合,其物理意义可能不直观,难以直接解释。
- 维度选择:选择合适的降维维度 k 是关键。可以通过查看特征值的累计贡献率来确定 k,一般选择累计贡献率达到 80% - 95% 的主成分。
四、示例及代码
以下是一个使用Python和scikit-learn库对鸢尾花数据集进行PCA降维和可视化的示例:
Python脚本
# 导入 numpy 库,用于进行高效的数值计算,np 是 numpy 常用的别名
import numpy as np
# 导入 matplotlib 库的 pyplot 模块,
# 用于创建各种可视化图表,plt 是 pyplot 常用的别名
import matplotlib.pyplot as plt
# 从 sklearn 库的 datasets 模块中导入 load_iris 函数,用于加载鸢尾花数据集
from sklearn.datasets import load_iris
# 从 sklearn 库的 preprocessing 模块中导入 StandardScaler 类,
# 用于对数据进行标准化处理
from sklearn.preprocessing import StandardScaler
# 从 sklearn 库的 decomposition 模块中导入 PCA 类,用于执行主成分分析(PCA)
from sklearn.decomposition import PCA
# 设置支持中文的字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
def perform_pca_visualization():
"""
此函数用于加载鸢尾花数据集,进行标准化处理,执行 PCA 降维,并可视化结果。
"""
try:
# 调用 load_iris 函数加载鸢尾花数据集,并将其赋值给变量 iris
iris = load_iris()
# 从加载的鸢尾花数据集中提取特征数据(如花瓣长度、宽度等),赋值给变量 X
X = iris.data
# 从加载的鸢尾花数据集中提取目标标签(即鸢尾花的类别),赋值给变量 y
y = iris.target
# 创建 StandardScaler 类的一个实例,用于后续的数据标准化操作
scaler = StandardScaler()
# 调用 scaler 的 fit_transform 方法,对特征数据 X 进行标准化处理
# fit_transform 会先计算 X 的均值和标准差,
# 然后将 X 转换为均值为 0、标准差为 1 的数据
# 标准化后的数据赋值给变量 X_scaled
X_scaled = scaler.fit_transform(X)
# 创建 PCA 类的一个实例,通过 n_components 参数指定降维后的维度为 2
# 意味着将把原始数据从高维空间降到 2 维空间
pca = PCA(n_components=2)
# 调用 pca 的 fit_transform 方法,对标准化后的数据 X_scaled 进行 PCA 降维操作
# 该方法会先找到数据的主成分,然后将数据投影到这些主成分上
# 降维后的数据赋值给变量 X_pca
X_pca = pca.fit_transform(X_scaled)
# 获取 PCA 降维后每个主成分的方差解释比例,赋值给变量 explained_variance_ratio
# 方差解释比例表示每个主成分所包含的原始数据的信息量占比
explained_variance_ratio = pca.explained_variance_ratio_
# 打印主成分的方差解释比例,方便查看每个主成分的重要程度
print("主成分的方差解释比例:", explained_variance_ratio)
# 使用 numpy 的 cumsum 函数计算主成分方差解释比例的累计值
# 即前 k 个主成分的方差解释比例之和,赋值给变量 cumulative_explained_variance
cumulative_explained_variance = np.cumsum(explained_variance_ratio)
# 打印累计方差解释比例,帮助判断前 k 个主成分保留了多少原始数据的信息
print("累计方差解释比例:", cumulative_explained_variance)
# 使用 matplotlib 的 figure 函数创建一个新的图形窗口,设置窗口大小为 8x6 英寸
plt.figure(figsize=(8, 6))
# 使用 matplotlib 的 scatter 函数绘制散点图
# X_pca[:, 0] 作为 x 轴数据,X_pca[:, 1] 作为 y 轴数据
# c=y 表示根据目标标签 y 对散点进行颜色编码,cmap='viridis' 指定颜色映射方案
# 该函数返回一个 PathCollection 对象,赋值给变量 scatter
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
# 设置 x 轴的标签为“第一主成分”
plt.xlabel('第一主成分')
# 设置 y 轴的标签为“第二主成分”
plt.ylabel('第二主成分')
# 设置图形的标题为“PCA 降维后的鸢尾花数据集”
plt.title('PCA 降维后的鸢尾花数据集')
# 调用 scatter 的 legend_elements 方法生成图例元素,
# 然后使用 plt.legend 创建图例
# title="类别" 设置图例的标题为“类别”,返回的图例对象赋值给变量 legend
legend = plt.legend(*scatter.legend_elements(), title="类别")
# 使用 plt.gca() 获取当前的坐标轴对象,然后将图例添加到该坐标轴上
plt.gca().add_artist(legend)
# 在图形中添加网格线,方便观察散点的位置
plt.grid(True)
# 调用 matplotlib 的 tight_layout 函数自动调整图形的布局,
# 确保所有元素都能完整显示
plt.tight_layout()
# 显示绘制好的图形
plt.show()
except Exception as e:
# 如果在执行上述代码过程中出现异常,捕获该异常并打印错误信息
print(f"执行过程中出现错误: {e}")
# 这是 Python 脚本的主程序入口
# 当脚本作为主程序直接运行时,会执行 perform_pca_visualization 函数
if __name__ == "__main__":
perform_pca_visualization()输出 / 打印结果注释
1. 主成分的方差解释比例
plaintext
主成分的方差解释比例: [0.92461872 0.05306648]
- 这里输出的是一个包含两个元素的数组,每个元素代表一个主成分的方差解释比例。第一个主成分解释了约 92.46% 的原始数据方差,说明它包含了原始数据中大部分的信息;第二个主成分解释了约 5.31% 的方差,包含的信息相对较少。
2. 累计方差解释比例
plaintext
累计方差解释比例: [0.92461872 0.9776852 ]
- 同样是一个包含两个元素的数组。第一个元素和主成分的方差解释比例中的第一个元素相同,因为它就是第一个主成分的方差解释比例;第二个元素是前两个主成分的方差解释比例之和,约为 97.77%,这意味着通过将数据降到 2 维,我们保留了原始数据约 97.77% 的信息。
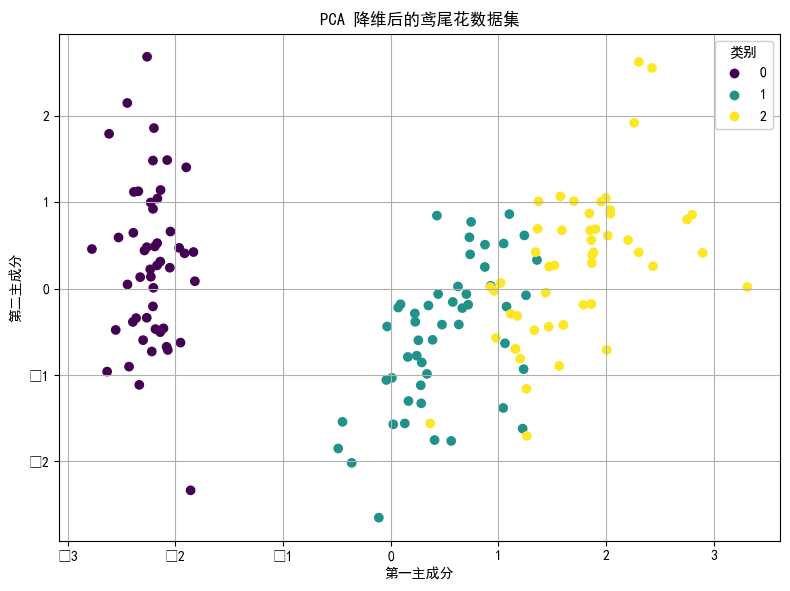
3. 可视化结果
运行代码后会弹出一个窗口显示散点图。图中不同颜色的散点代表不同类别的鸢尾花,x 轴是第一主成分,y 轴是第二主成分。通过这个散点图,可以直观地看到经过 PCA 降维后,不同类别鸢尾花在二维空间中的分布情况。
重点语句解读
1、数据加载:
Python脚本
iris = load_iris()
X = iris.data
y = iris.target- 这部分代码使用 load_iris 函数从 sklearn.datasets 中加载鸢尾花数据集,X 是特征矩阵,y 是目标标签。
2、数据标准化:
Python脚本
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)- StandardScaler 用于对数据进行标准化处理,使数据的均值为 0,标准差为 1。fit_transform 方法先计算数据的均值和标准差,然后进行标准化转换。
3、创建 PCA 对象并降维:
Python脚本
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)- PCA(n_components = 2) 创建一个 PCA 对象,指定降维后的维度为 2。fit_transform 方法对标准化后的数据进行 PCA 分析,并将数据投影到前两个主成分上。
4、方差解释比例:
Python脚本
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_explained_variance = np.cumsum(explained_variance_ratio)- explained_variance_ratio_ 属性返回每个主成分的方差解释比例,np.cumsum 函数用于计算累计方差解释比例,帮助我们了解每个主成分和前 k 个主成分保留的信息比例。
5、可视化:
Python脚本
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
legend = plt.legend(*scatter.legend_elements(), title="类别")- plt.scatter 绘制散点图,c = y 根据目标标签对散点进行颜色编码,cmap = 'viridis' 选择颜色映射。scatter.legend_elements() 生成图例元素,plt.legend 添加图例。
——The END——
🔗 欢迎订阅专栏
| 序号 | 专栏名称 | 说明 |
|---|---|---|
| 1 | 用Python进行AI数据分析进阶教程 | 《用Python进行AI数据分析进阶教程》专栏 |
| 2 | AI大模型应用实践进阶教程 | 《AI大模型应用实践进阶教程》专栏 |
| 3 | Python编程知识集锦 | 《Python编程知识集锦》专栏 |
| 4 | 字节跳动旗下AI制作抖音视频 | 《字节跳动旗下AI制作抖音视频》专栏 |
| 5 | 智能辅助驾驶 | 《智能辅助驾驶》专栏 |
| 6 | 工具软件及IT技术集锦 | 《工具软件及IT技术集锦》专栏 |
👉 关注我 @理工男大辉郎 获取实时更新
欢迎关注、收藏或转发。
敬请关注 我的
微信搜索公众号:cnFuJH
CSDN博客:理工男大辉郎
抖音号:31580422589

GitCode 天启AI是一款由 GitCode 团队打造的智能助手,基于先进的LLM(大语言模型)与多智能体 Agent 技术构建,致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话,还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力,真正做到“一句话,让 Al帮你完成复杂任务”。
更多推荐
 已为社区贡献10条内容
已为社区贡献10条内容









所有评论(0)