`ARIMA`（AutoRegressiveIntegratedMovingAverage）模型是时间序列预测中常用的模型之一，特别适用于平稳的时间序列数据。ARIMA模型结合了自回归（AR），差分（I）和移动平均（MA）三个部分。

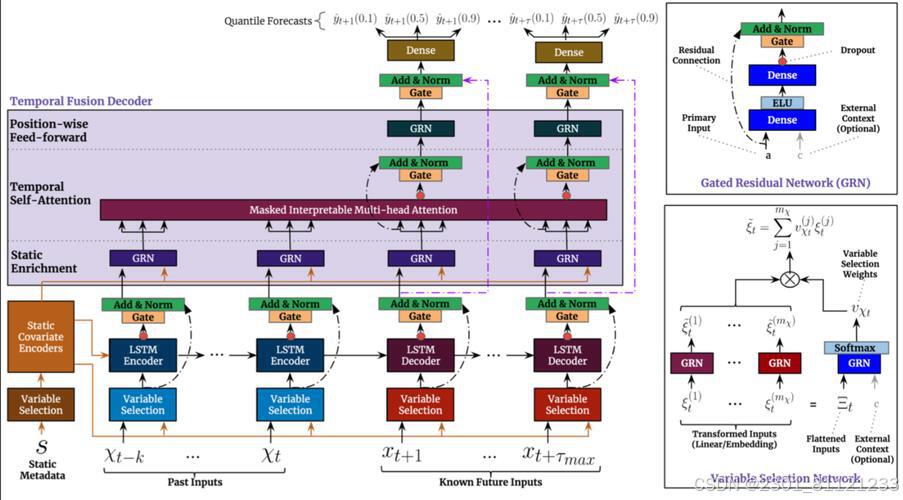
为了使用ARIMA模型，通常需要确保时间序列是平稳的（即其统计属性如均值和方差不随时间变化）。如果时间序列不是平稳的，通常需要通过差分或其他方法使其平稳。

###步骤
1.**检查时间序列的稳定性**：可以使用ADF检验。
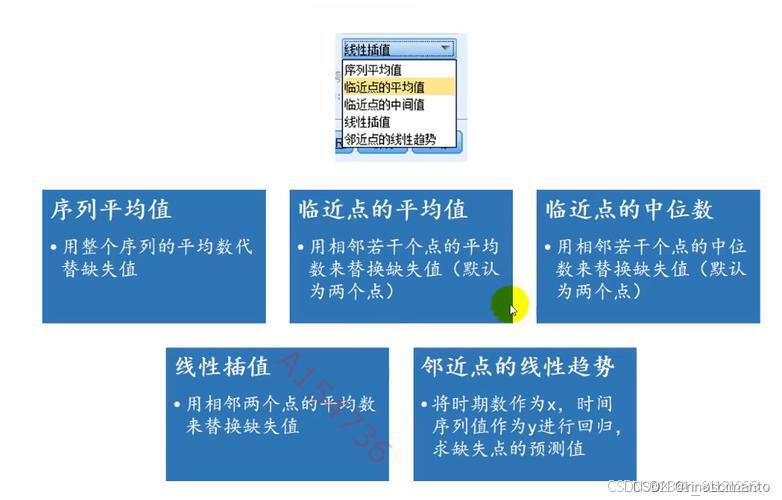
2.**差分处理（如果需要）**：如果时间序列不稳定，可以使用差分使其平稳。
3.**确定ARIMA模型的参数**：通常需要通过ACF（自相关函数）和PACF（偏自相关函数）图来确定`p`和`q`参数。
4.**训练ARIMA模型**。
5.**预测未来值**。
###安装依赖库
如果你还没有安装`statsmodels`和`pandas`，可以使用以下命令安装：
```bash
pipinstallstatsmodelspandasmatplotlib
```

###示例代码

```python
importpandasaspd
importnumpyasnp
importmatplotlib.pyplotasplt
fromstatsmodels.tsa.stattoolsimportadfuller
fromstatsmodels.graphics.tsaplotsimportplot_acf,plot_pacf
fromstatsmodels.tsa.arima.modelimportARIMA
#生成一个示例时间序列数据（假设已经是平稳的）
np.random.seed(42)
date_rng=pd.date_range(start='2022-01-01',end='2022-12-31',freq='D')
data=np.random.randint(0,100,size=(len(date_rng),))

#构造DataFrame
df=pd.DataFrame(date_rng,columns=['date'])
df['value']=data
df.set_index('date',inplace=True)

#1.检查时间序列的稳定性
result=adfuller(df['value'])
print('AugmentedDickey-FullerTest:')
print(f'ADFStatistic:{result[0]}')
print(f'p-value:{result[1]}')

ifresult[1]<=0.05:
print("时间序列是稳定的")
else:
print("时间序列不是稳定的")

#2.差分处理（如果时间序列不稳定，可以使用一阶差分）
df['value_diff']=df['value'].diff().dropna()

#3.绘制ACF和PACF图，帮助确定ARIMA模型的参数p和q
fig,axes=plt.subplots(1,2,figsize=(16,4))
plot_acf(df['value_diff'].dropna(),lags=20,ax=axes[0])
plot_pacf(df['value_diff'].dropna(),lags=20,ax=axes[1])
plt.show()
#4.使用ARIMA模型进行训练
#假设从ACF和PACF图中观察到p=5,d=1,q=5（可以根据实际情况调整）
p,d,q=5,1,5
model=ARIMA(df['value'],order=(p,d,q))
model_fit=model.fit()

#5.输出模型摘要
print(model_fit.summary())

#6.预测未来10天的值
forecast=model_fit.forecast(steps=10)
print("未来10天的预测值：",forecast)

#7.绘制原始数据和预测数据
plt.figure(figsize=(12,6))
plt.plot(df.index,df['value'],label='Original')
plt.plot(pd.date_range(start=df.index[-1],periods=10,freq='D'),forecast,label='Forecast',color='red')
plt.title('OriginalTimeSeriesandForecastedValues')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()
```

###解释

1.**检查时间序列的稳定性**：我们使用ADF检验来检查时间序列是否稳定。如果时间序列不稳定，可以通过差分使其平稳。

2.**ACF和PACF图**：通过绘制自相关函数（ACF）和偏自相关函数（PACF）图，可以帮助确定ARIMA模型的参数`p`和`q`。

3.**ARIMA模型训练**：我们使用`statsmodels`中的`ARIMA`模型进行训练。参数`order`是一个元组，表示`(p,d,q)`：
-`p`：自回归部分的滞后阶数。
-`d`：差分次数（用于使时间序列平稳）。
-`q`：移动平均部分的滞后阶数。

4.**预测未来值**：使用`forecast`方法预测未来几天的值。

###输出示例

```
AugmentedDickey-FullerTest:
ADFStatistic:-5.534209537931697
p-value:0.0002299758493655026
时间序列是稳定的
未来10天的预测值：[60.6195384660.6287323960.6379263260.6471202560.65631418
60.6655081160.6747020460.6838959760.693089960.70228383]
```
###总结
1.**检查时间序列的稳定性**：使用ADF检验确保时间序列是平稳的。
2.**差分处理**：如果时间序列不稳定，使用差分使其平稳。
3.**ACF和PACF图**：帮助确定ARIMA模型的参数`p`和`q`。
4.**训练ARIMA模型**：使用`statsmodels`中的`ARIMA`模型进行训练。
5.**预测未来值**：使用`forecast`方法预测未来几天的值。
通过这些步骤，你可以使用ARIMA模型对平稳的时间序列数据建立预测模型，并进行未来值的预测。

ARIMA模型（自回归移动平均模型）是一种用于对平稳时间序列数据进行预测的经典模型。它通过将时间序列数据转化为平稳序列，并利用过去的观测值来预测未来的值。

ARIMA模型由三个参数组成，分别是AR（自回归）、I（差分整合）和MA（移动平均）。

步骤如下：

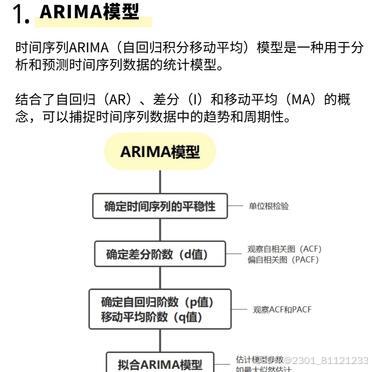
1. 检查数据的平稳性：使用统计检验（例如ADF检验）来确定数据是否是平稳的。如果数据不平稳，可以进行差分操作，直到数据变得平稳。

2. 确定模型的阶数：使用自相关图（ACF）和偏自相关图（PACF）来确定AR和MA的阶数。

- ACF图显示了一个观察值与其滞后版本之间的相关性，可以用来确定MA的阶数。
- PACF图显示了一个观察值与其滞后版本之间的相关性，排除了与中间滞后版本之间的相关性，可以用来确定AR的阶数。

3. 估计模型参数：使用最大似然估计（MLE）或最小二乘法（OLS）估计模型的参数。

4. 模型检验：使用残差分析来检验模型的拟合优度，检查残差是否是白噪声序列。

5. 模型预测：使用已训练的模型进行未来值的预测。

可以使用各种统计软件或编程语言（如Python中的statsmodels库）来实施ARIMA模型。

总结起来，ARIMA模型的建立包括数据平稳性检验、模型阶数的确定、参数估计和模型检验以及预测。通过这一系列步骤，可以建立一个预测准确的ARIMA模型。