【加解密算法实现】全面剖析RSA加解密算法（附完整C/Python源码）

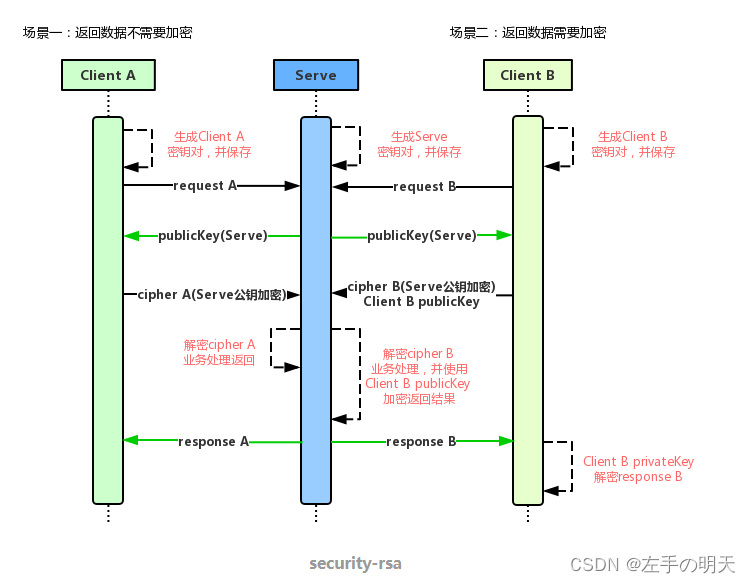
公开密钥加密(public-key cryptography),也成为非对称加密，是密码学的一种算法，他需要两个密钥，一个是公开密钥，另一个是私有密钥，一个用作加密的时候，另一个则用作解密。

左手の明天

1170人浏览 · 2022-05-01 20:27:56

左手の明天 · 2022-05-01 20:27:56 发布

🔗运行环境：C、Python
🚩创作作者：左手の明天
🥇精选专栏：python
🔥 推荐专栏：算法研究
——————————————————————————

💗 大家好🤗🤗🤗，我是左手の明天！💗

📆 最近更新：2022 年 5 月 1 日，左手の明天的第 236 篇原创博客

📚 更新于专栏：算法研究
——————————————————————————

🌟🌟今天是五一劳动节，在这里左手の明天祝大家节日快乐🌟🌟

在这里插入图片描述

🚩1 前言

密码学和安全协议是通信系统安全的技术核心。传统的密码技术主要是建立在基本的替代和置换工具上的对称密钥加密技术，包括有 DES，3DES，IDEA，AES，Blowfish 等。Diffie 和 Hellman 在1976年首次公开引进公开密钥密码技术的概念，但并没有给出一种有效的算法，直到两年后由 MIT（麻省理工学院）的 Ron Rivest，Adi Shamir 和 Len Aleman 提出了 RSA 的通用公开加密方法，从而使得公开加密技术在国防、商业上获得越来越广泛的应用，国际上ISO，ITU，SWIFT 等标准化组织已把 RSA 体制作为标准。

RSA 密码体制是目前较流行的一种公钥密码算法。

🚩2 公钥密码算法理论

公钥密码学的提出是为了解决对称密码学中密钥分配和数字签名两个难题。1976 年 Diffe 和Hellman 首次公开提出了公钥密码学的概念，并设计了在不安全公共网络上进行安全传输密钥的协议问题。公钥密码学系统的安全性是基于单向陷门函数的安全性,所谓单向陷门函数就是正向计算函数值很容易，在缺少附加信息时计算函数的逆是不可行的，一般满足下列条件：

1）若 k 和 X 已知，则可计算 $Y = f_{k}(X)$
2）若 k 和 Y 已知，则可计算 $X = f_{k}(Y)$
3）若 Y 已知，但 k 未知，则计算出 $X = f_{k}^{-1}(Y)$ 不可行。

⭐️2.1 公钥密码体系

从集合论角度看，一个公钥密码系统可以定义为一个九元组集合：{M,C,K,m,X,e,d,E,D}

1）M 为明文集合，或称作明文空间；
2）C 为密文集合，或称作密文空间；
3）K 为密钥集合，或称作密钥空间；
4）m∈M，是明文集合的一个子集；
5）X∈C，是密文集合的一个子集；
6）e为公钥，d为私钥，(e,d)∈K，且 e≠d；
7）E为加密函数，D为解密函数；由于 m∈M，X∈C，使用公钥 $e_{k}$ ，加密如下：
$X=E_{e_{k}}(m)$
8）D为解密函数，使用私钥 $d_{k}$ ，则：
$X=D_{d_{k}}(m)$
满足：
$D_{d_{k}}(X)=D_{d_{k}}(E_{e_{k}}(m))=M$

⭐️2.2 公钥密码系统工作原理

公钥密码系统工作原理如图所示：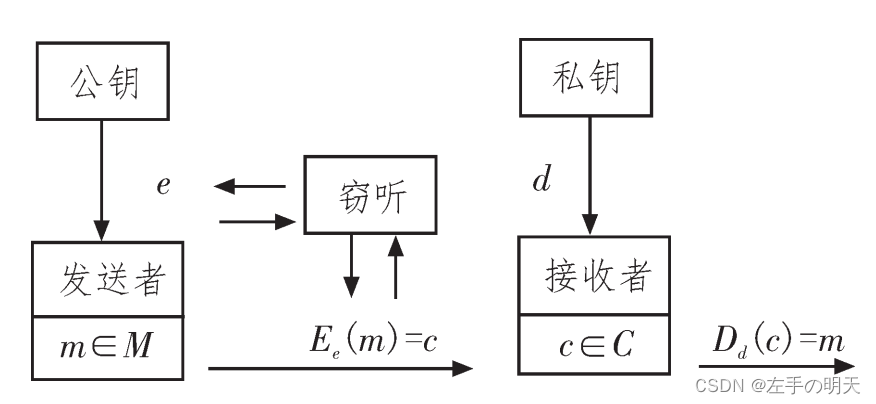
在这里插入图片描述

🚩3 RSA密码算法

⭐️3.1 RSA 公钥密码系统工作流程

RSA 密码体制属于分组密码，是目前最流行、应用最广泛的公钥密码系统。假设 Bob向 Alice发送消息，RSA 公钥密码系统工作流程如图所示：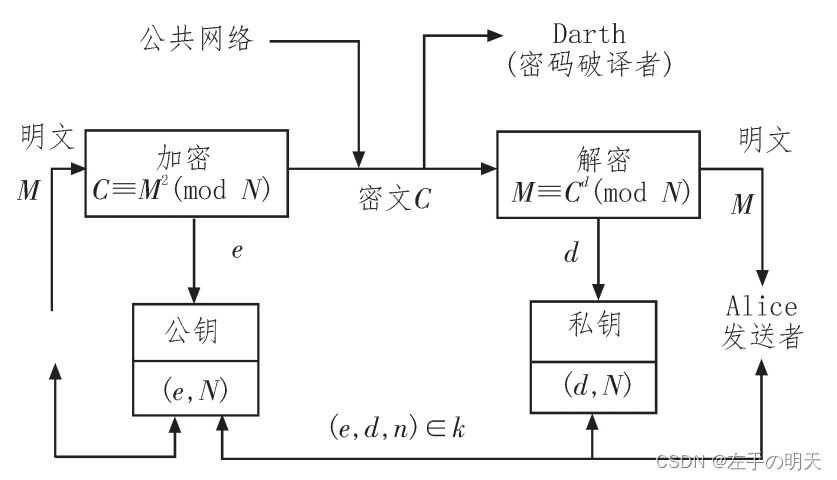
在这里插入图片描述
RSA密码算法可以假设为一个八元组：{M，C，K，e，d，N，E，D}

1）M 为明文空间；
2）C 为密文空间；
3）K 为密钥空间；
4）e为公钥，d为私钥；
5）E 为加密函数；
6）D 为解密函数；
7）N 为 p 和 q 两个大素数之积，且 p、q 位数不小于 100，{(e,N),(d,N)}∈K 且 e≠d，同时满足 ed≡1(modφ(N))，φ(N)=(p-1)(q-1)。

⭐️3.2 RSA密钥对生成

RSA算法产生密钥的过程：

Bob 随机生成两个大小相当的大素数p, q（保密），且 p≠q；
计算n=pq（公开），欧拉函数Φ(n)=(p-1)(q-1)(保密) ，这里的整数 n 是RSA 算法的模；
Bob 再选择一个随机数 e∈N，这样 1<e<φ(n)，gcd(e,Φ(n))=1的e作为公钥(公开)，加密密钥就是(e,n) ；
使用扩展欧几里德算法，计算出 d∈N,且 1<d<φ(n),计算满足ed=1(mod Φ(n))的d作为私钥(保密)，解密密钥即为(d,n) 。

⭐️3.3 RSA加密算法

假设明文消息 m∈M 是数值形式，且 m<n， $M= C=Z/Z_{n}$ ，假设 gcd(m, n)≡1。

加密时首先将明文比特串进行分组，使得每个分组对应的串在数值上小于 N，即分组的二进制长度小于 1092 N。然后，对每个明文分组 m，作加密运算。过程如下：

1）Bob通过公共数据库获得 Alice的公钥(n,e)；
2）Bob通过加密算法对消息 m 进行加密， $c≡m^{e}(modn)$ ，其中 m 为明文，c 为密文。；
3）Bob发送 c∈X给 Alice。

⭐️3.4 RSA解密算法

当 Alice 接收到加密消息 c 时，使用私钥 d 和要加密的明文 m 进行 $m≡c^{d}(modn)$ 进行计算。

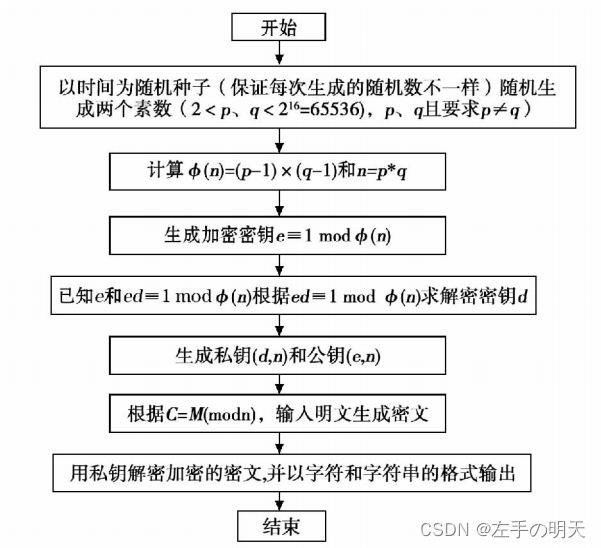
在这里插入图片描述

⭐️3.5 RSA算法实例

取p=47， q=71，则n = p * q = 3337， Φ(n)=(p-1)(q-1)=3220，随机选择加密密钥e，e与Φ(n)互素，若取e=79，则 d=79-1(mod n)=1019。

假设要加密的明文是m=6882326879666683，首先，根据n的大小将m进行分组，这里我们把明文m分成六个组，即：

m1=688，m2=232，m3=687，m4=966，m5=668，m6=003

接着分别对各个分组进行加密运算，第一个分组加密为

c1=68879(mod 3337) = 1570

类似的，对其余各个分组分别进行加密运算，得到如下密文：

c=1570 2756 2091 2276 2423 158

解密时用私钥1019分别对明文进行解密运算，即：

m1=15701019(mod 3337) = 688

对其余的密文用同样的计算方法就可以把密文恢复出来，即得到密文。

⭐️3.6 RSA数字签名算法

RSA 的主要应用之一是数字签名，数字签名是一种将信息绑定到实体的机制，并且包含一个验证过程。

1）初始化阶段
Alice 发送消息给 Bob，从 RSA 密钥空间 k={n, p, q, e, d}选择签名所需要的各种参数。
2）签名
Alice的私有数字签名 Sigk由下式生成：
$Sig_{k}(m)≡md≡c (mod n)$ Verk 是它的公共验证算法，然后它发送 (m, c)给 Bob。
3）验证
Bob 获得 Alice 的公钥及签名信息(e, Verk)，计算
$Ver_{k}(m, c)$ ，当 $m≡c^{e}(mod n)$ 时， $Ver_{k}(m, c)$ 正好是 1，在这种情况下，Bob接受签名，否则拒绝它。

🚩4 RSA实现（C语言）

⭐️4.1 大数的加法运算

目前在 32 位机器上能表示的最大整数只有 $2^{32}-1$ ，RSA 中几百位甚至上千位的大数的加法运算用一般机器上定义的加法运算是无法满足的，必须定义与大数存储方式符合的运算方式来计算大数相加。

void Plus(byteint A,byteint B,byteint C) 
{ 
	register i; 
	int X,m,n,valid; 
	m=Int Valid(A); 
	n=Int Valid(B); 
	valid=(m>n)?m+1:n+1; 
	Set Zero(C); 
	for(i=Data Length-1;i>=Data Length-valid;i--) 
	{ 
		X=C[i]+A[i]+B[i]; 
		C[i]=X%10; 
		if(X>9) 
			C[i-1]=C[i-1]+X/10; 
	} 
}

函数的功能是计算 A+B，并将计算结果保存到 C 中。

byteint 是我们自己定义的特定的数据结构，用来存储大数；
Int Valid(A)为计算大数 A 的十进制长度；
Set Zero(C ) 是将大数 C 置为零；
C[i]、A[i]、B[i]对应大数 C、A、B 第 i 个单元的值。

大数加法运算的原理与普通的加法计算一样，是从低位单元依次相加，若有进位则将进位 1 先加到C 的高一个单元中，最后计算的结果存放在 C 中。

⭐️4.2 大数的减法运算

同大数的加法运算一样，也必须自己定义大数的减法运算。

void Substract(byteint SA,byteint SB,byteint SC) 
{ 
  byteint buf; 
  register i,j; 
  Int Cpy(buf,SA); 
  Set Zero(SC); 
  for(i=Data Length-1;i>=0;i--)  
  { 
   if(buf[i]<SB[i]) 
   { 
    buf[i]=buf[i]+10; 
     j=i-1; 
     while(buf[j]==0) 
      buf[j--]=9; 
     buf[j]=buf[j]-1; 
   } 
   SC[i]=buf[i]-SB[i];  
  } 
}

函数的功能是计算 SA-SB，并将计算结果保存到 SC 中，参数要求SA ≥SB 。

其中Int Cpy(buf,SA)是将 SA 拷贝到 buf 中。

大数减法运算的原理与普通的减法计算一样，是从低位单元依次相减，若低位单元不够减则向高位单元借 1 化作 10 个低位单元，并将高位的单元减 1，最后计算的结果存放在 SC 中。

⭐️4.3 大数的乘法运算

同大数的加法运算一样，也必须自己定义大数的乘法运算。

void Multiply(byteint A,byteint B,byteint C) 
{ 
  register i,j,w; 
  int X; 
  int Avalid=0;    
  int Bvalid=0; 
  while (A[Avalid]==0 && Avalid<Data Length) 
  	Avalid++; 
  while (B[Bvalid]==0 && Bvalid<Data Length) 
  	Bvalid++; 
  Set Zero(C); 
  for(i=Data Length-1;i>=Avalid;i--) 
   for(j=Data Length-1;j>=Bvalid;j--)  
   { 
    w=i+j-(Data Length-1); 
    X=C[w]+A[i]*B[j];               
    C[w]=X%10; 
    C[w-1]=C[w-1]+X/10;    
   } 
}

函数的功能是计算 A×B ，并将计算结果保存到 C 中。

由于大数的存储采用一个单元存储大数的一个十进制位，这与我们日常生活中计算整数的乘法是一样的形式，因此非常容易理解上述的伪代码。大数乘法运算的原理与普通的乘法计算一样，是从乘数 B的低位单元依次与 A 相乘，产生的进位保存在高一位的存储单元内。

⭐️4.4 大数的除法运算

同大数的其它运算一样，也必须自己定义大数的除法运算。

void Divide(byteint A,byteint B,byteint C,byteint D) 
{ 
  register i,j; 
  int valid_1,valid_2,valid,sbits,cmpval; 
  byteint buf1,buf2; 
  Set Zero(D);  
    Int Cpy(C,A);  
  valid_2=Int Valid(B); 
  while((cmpval=Int Cmp(C,B))>0)  
  { 
   valid_1=Int Valid(C);  
   valid=valid_1-valid_2;  
   if(valid>0)  
   { 
    i=Data Length-valid_1;  
    j=Data Length-valid_2;  
    sbits=0; 
    while(j<Data Length) 
    { 
     if(C[i]>B[j])  
      break; 
     if(C[i]<B[j]) 
     { 
      sbits=1; 
      break; 
     } 
     i++; j++; 
    } 
    valid=valid-sbits; 
    Set Zero(buf1);             
    for(i=Data Length-valid_2;i<Data Length;i++) 
    { 
     j=i-valid; 
     buf1[j]=B[i]; 
    } 
   } 
   else 
    Int Cpy(buf1,B); 
   D[Data Length-1-valid]++; 
   Substract(C,buf1,buf2); 
   Int Cpy(C,buf2); 
  } 
  if(cmpval==0) 
  { 
   Set Zero(C); 
   D[Data Length-1]++; 
  } 
}

函数的功能是计算 A÷B ，并将余数保存在 C 中，商保存在 D 中。

上述大数的除法运算的原理与普通整数的除法计算不太一样，是从被除数 A 的高位单元开始取与除数 B相同长度的单元与 B 循环做减法，直到不够减时再退一位，每次够减时在商 D 中相应的单元中加 1。

⭐️4.5 完整代码

RSA.C：源码内容

#include <windows.h>
#include <dos.h>
#include <conio.h>
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <time.h>
#define DATALENGTH 350
#define MLENGTH 10
#define TESTNUM 20
#define SKLENGTH 5
#define TEXTLENGTH 20
typedef signed char byteint[DATALENGTH]; //-128 ->127
typedef signed char mtype[MLENGTH];
mtype Model[TESTNUM];
byteint ONEVALUE,ZEROVALUE,TWOVALUE,EIGHTVALUE;
void InitInt(void);
void SetZero(byteint A);
void IntCpy(byteint A,byteint B);
int IntValid(byteint validtemp);
int IntCmp(byteint A,byteint B);
void Plus(byteint A,byteint B,byteint C);
void Substract(byteint SA,byteint SB,byteint SC);
void Multiply(byteint A,byteint B,byteint C);
void SetMode(byteint A,byteint B,byteint C,byteint D);
void IntRandom(byteint RandomA,int num);
void LoadInt(byteint A,mtype B);
void Mdata(void);
void TransBi(byteint B,signed char flag[400]);
int PowerMode(byteint A,byteint C,byteint D,signed char flag[400]);
int Prime(byteint Prm);
int ComputingPK(byteint Rvalue,byteint SK,byteint PK);
int StrToByt(char *str,byteint byt);
void BytToStr(byteint byt,char *str);
void PackInt(byteint A,int B);
byteint R,SK,PK,RsaKey; 
extern int ShoutBlockingHook (void);
extern char szDataPath[128];

int RsaPrepare(byteint sk,byteint pk,byteint r)
{
	byteint p,q,Rvalue,buf1,buf2;
	Mdata();
	InitInt();
	Prime(p);
	Prime(q);
	Multiply(p,q,r);
	Substract(p,ONEVALUE,buf1);
	Substract(q,ONEVALUE,buf2);
	Multiply(buf1,buf2,Rvalue);
	ComputingPK(Rvalue,sk,pk); 
	return TRUE;
}

int ReadRsaFile(byteint r,byteint pk,byteint sk)
{
	char file[80],temp[100+1];
	sprintf(file,"%s\sys\rsa.dat",szDataPath);
	if(GetPrivateProfileString("RSA", "R", "", temp,100, file)!=0)
		StrToByt(temp,r);
	else
		return FALSE;
	if(GetPrivateProfileString("RSA", "PK", "", temp, 100, file)!=0)
		StrToByt(temp,pk);
	else
		return FALSE;
	if(GetPrivateProfileString("RSA", "SK", "", temp, 100, file)!=0)
		StrToByt(temp,sk);
	else
		return FALSE;
	return TRUE;
}

int WriteRsaFile(byteint r,byteint pk,byteint sk)
{
	char file[80],temp[100+1];
	sprintf(file,"%s\sys\rsa.dat",szDataPath);
	memset(temp,0,100+1);
	BytToStr(r,temp);
	if(WritePrivateProfileString("RSA", "R", temp, file)==0)
		return FALSE;
	memset(temp,0,100+1);
	BytToStr(pk,temp);
	if(WritePrivateProfileString("RSA", "PK", temp, file)==0)
		return FALSE;
	memset(temp,0,100+1);
	BytToStr(sk,temp);
	if(WritePrivateProfileString("RSA", "SK", temp, file)==0)
		return FALSE;
	return TRUE;
}

int DecipherDesKey(byteint rsakey,byteint r,byteint sk,char *deskey)
{
	byteint buf1;
	signed char flag[400];
	Mdata();
	InitInt();
	TransBi(sk,flag);
	PowerMode(rsakey,r,buf1,flag);
    BytToStr(buf1,deskey);
    
return 0;
}
void InitInt(void)
{
	SetZero(ONEVALUE);
	ONEVALUE[DATALENGTH-1]=1;
	SetZero(ZEROVALUE);
	SetZero(TWOVALUE);
	TWOVALUE[DATALENGTH-1]=2;
	SetZero(EIGHTVALUE);
	EIGHTVALUE[DATALENGTH-1]=8;
	//randomize();
	srand((unsigned)time(NULL));
}

void Multiply(byteint A,byteint B,byteint C)
{
	register i,j,w;
	int X,Y,Z;
	int Avalid=0;
	int Bvalid=0;
	while(A[Avalid]==0 &&Avalid <DATALENGTH)
		Avalid++;
	while(B[Bvalid]==0 &&Bvalid <DATALENGTH)
		Bvalid++;
	SetZero(C);
	for(i=DATALENGTH -1;i>=Avalid;i--)
	{
		for(j=DATALENGTH-1;j>=Bvalid;j--)
		{
			X=A[i]*B[j];
			Y=X/10;
			Z=X-10*Y;
			w=i+j-(DATALENGTH-1);
			C[w]=C[w]+Z;
			C[w-1]=C[w-1]+(C[w]/10)+Y;
			C[w]=C[w]-(C[w]/10)*10;
		}
	}
}

void SetZero(byteint A)
{
	memset(A,0,DATALENGTH);
}
void IntCpy(byteint A,byteint B)
{
	memcpy(A,B,DATALENGTH);
}
void Plus(byteint A,byteint B,byteint C)
{
	register i;
	int X,Y,Z,m,n,valid;
	m=IntValid(A);
	n=IntValid(B);
	valid=(m>n) ? m+1:n+1;
	SetZero(C);
	for(i=DATALENGTH -1;i>=DATALENGTH -valid;i--)
	{
		X=A[i] +B[i];
		Y=X/10;
		Z=X-10*Y;
		C[i]=C[i]+Z;
		C[i-1]=C[i-1]+Y;
	}
}
void Substract(byteint SA,byteint SB,byteint SC)
{
	byteint buf;
	register i,j;
	int X;
	IntCpy(buf,SA);
	SetZero(SC);
	for(i=DATALENGTH-1;i>=0;i--)
	{
		if(buf[i]<SB[i]){
			buf[i]+=10;
			if(buf[i-1]>0)
				(buf[i-1])--;
			else {
				j=i-1;
				while (buf[j]==0)
					buf[j--]=9;
					buf[j]--;
			}
		}
		X=buf[i]-SB[i];
		SC[i]=X;
	}
}
int IntCmp(byteint A,byteint B)
{
	int stat;
	stat =memcmp(A,B,DATALENGTH);
	if(stat ==0)
		return 0;
	if(stat>0)
		return 1;
	return -1;
}
int IntValid(byteint validtemp)
{
	register i=0;
	while (validtemp[i]==0 && i<DATALENGTH)
		i++;
	return DATALENGTH-i;
}
void SetMode(byteint A,byteint B,byteint C,byteint D)
{
	register i,j,k;
	int valid_1,valid_2,valid,sbits,cmpval;
	byteint buf1,buf2;
	SetZero(D);
	IntCpy(C,A);
	valid_2=IntValid(B);
	while((cmpval =IntCmp(C,B))>0){
		valid_1 =IntValid(C);
		valid =valid_1-valid_2;
		if(valid>0){
			i=DATALENGTH -valid_1;
			j=DATALENGTH -valid_2;
			sbits=0;
			for(k=j;k<DATALENGTH;k++){
				if(C[i]>B[j])
					break;
				if(C[i]<B[j]){
					sbits=1;
					break;
				}
				i++;j++;
			}
			valid=valid -sbits;
			SetZero(buf1);
			for(i=valid;i<DATALENGTH;i++){
				j=i-valid;
				buf1[j]=B[i];
			}
		}
		else
			IntCpy(buf1,B);
			D[DATALENGTH-1-valid]++;
			Substract(C,buf1,buf2);
			IntCpy(C,buf2);
	}
	if(cmpval==0){
		SetZero(C);
		D[DATALENGTH-1]++;
	}
}
void IntRandom(byteint RandomA,int num)
{
	int i;
	SetZero(RandomA);
	while(!(RandomA[DATALENGTH-1] % 2))
		RandomA[DATALENGTH-1]=rand() % 10;
	while(!RandomA[DATALENGTH-num])
		RandomA[DATALENGTH-num] =rand() % 10;
	i=DATALENGTH -2;
	while(i>=DATALENGTH -num +1)
		RandomA[i--]=rand() % 10;
}
void LoadInt(byteint A,mtype B)
{
	register i,j;
	SetZero(A);
	i=DATALENGTH -1;
	j=MLENGTH -1;
	while(j>=0)
		A[i--]=B[j--];
}
void Mdata(void)
{
	register i,j;
	int k=MLENGTH -2;
	memset(Model,0,TESTNUM*MLENGTH);
	for(i=0;i<TESTNUM;i++){
		for(j=MLENGTH-1;j>=k;j--)
			Model[i][j]=rand()%10;
			k-=1;
	}
}
void TransBi(byteint B,signed char flag[400])
{
	byteint buf;
	byteint result;
	byteint temp;
	register i;
	memset(flag,0,400);
	i=399;
	IntCpy(buf,B);
	while(IntCmp(buf,ZEROVALUE)==1){
		ShoutBlockingHook();
		SetMode(buf,TWOVALUE,temp,result);
		flag[i]=temp[DATALENGTH -1];
		IntCpy(buf,result);
		i--;
	}
	flag[i] =-1;
}
int PowerMode(byteint A,byteint C,byteint D,signed char flag[400])
{
	byteint buf;
	byteint result;
	byteint temp,P;
	register i;
	IntCpy(temp,A);
	if(flag[399]==1)
		IntCpy(result,A);
	else
		IntCpy(result,ONEVALUE);
	i=398;
	while(flag[i]!=-1){
		ShoutBlockingHook();
		Multiply(temp,temp,buf);
		SetMode(buf,C,temp,P);
		if(flag[i]!=0){
			Multiply(temp,result,buf);
			SetMode(buf,C,result,P);
		}
		i--;
	}
	IntCpy(buf,C);
	IntCpy(D,result);
	Substract(buf,ONEVALUE,temp);
	if(IntCmp(result,ONEVALUE)==0)
		return 1;
	if(IntCmp(result,temp)==0)
		return 2;
	return 0;
}
int Prime(byteint Prm)
{
	int i,k,ok,cnt=0;
	signed char flag[400];
	byteint A,B,D,buf1,buf2;
	int pass=0,pass_2=0;
	while(1){
		ShoutBlockingHook();
		cnt++;
		IntRandom(B,MLENGTH);
		IntCpy(Prm,B);
		Substract(B,ONEVALUE,buf1);
		SetMode(buf1,TWOVALUE,buf2,B);
		TransBi(B,flag);
		ok=1;
		for(i=0;i<TESTNUM;i++){
			LoadInt(A,Model[i]);
			k=PowerMode(A,Prm,D,flag);
			if(k!=1&&k!=2)
				break;
			if(k==2){
				pass_2=1;
			}
		}
		if(ok && pass_2 ){
			return 0;
		}
	}
}
int ComputingPK(byteint Rvalue,byteint SK,byteint PK)
{
	register i;
	byteint PA,PB,PC,buf,temp,buf2;
	SetZero(PK);
	while(1)
	{
		IntRandom(SK,SKLENGTH);
		IntCpy(PB,SK);
		IntCpy(PA,Rvalue);
		while(1) {
			ShoutBlockingHook();
			SetMode(PA,PB,PC,PK);
			i=IntCmp(PC,ONEVALUE);
			if(i==0)
				break;
			i=IntCmp(PC,ZEROVALUE);
			if(i==0){
				i=-1;
				break;
			}
			IntCpy(PA,PB);
			IntCpy(PB,PC);
		}
		if(i==0)
		break;
	}
	IntCpy(temp,ONEVALUE);
	IntCpy(PA,Rvalue);
	IntCpy(PB,SK);
	while (1){
		Multiply(PA,temp,buf);
		Plus(buf,ONEVALUE,buf2);
		SetMode(buf2,PB,buf,PK);
		if(IntCmp(buf,ZEROVALUE)==0)
			break;
		Plus(temp,ONEVALUE,buf);
		IntCpy(temp,buf);
	}
	return 1;
}
void PackInt(byteint A,int B)
{
	register i=DATALENGTH-1;
	SetZero(A);
	while(B>0){
		A[i--]=B % 10;
		B=B/10;
	}
}
int StrToByt(char *str,byteint byt)
{
	unsigned int m;
	SetZero(byt);
	for(m=0;m<strlen(str);m++)
		byt[DATALENGTH-1-m]=str[strlen(str)-m-1]-'0';
	return 1;
}
void BytToStr(byteint byt,char *str)
{
 	 unsigned  int i=0,j=0;
 	 while(i<DATALENGTH&&byt[i]==0) i++;
 	 for(;i<DATALENGTH;i++,j++)
 	 {
 		 str[j] =byt[i]+'0';
	 }
}

RSA.H：源码内容

#define DATALENGTH 350
signed char R[DATALENGTH],PK[DATALENGTH],RsaKey[DATALENGTH]; 
signed char SK[DATALENGTH];
unsigned char DesKey[9];
int RsaPrepare(signed char *sk,signed char *pk,signed char *r);
int ReadRsaFile(signed char *r,signed char *pk,signed char *sk);
int WriteRsaFile(signed char *r,signed char *pk,signed char *sk);
//int EncipherDesKey(char *deskey,signed char *r,signed char *pk,signed char *rsakey);
int DecipherDesKey(signed char *rsakey,signed char *r,signed char *sk,char *deskey);
int StrToByt(char *str,signed char *byt);
void BytToStr(signed char *byt,char *str);

🚩5 基于PyCryptodome的RSA设计与实现

PyCryptodome 是一个包含底层密码原语的 Python 包。

⭐️5.1 PyCryptodome库相关函数

1）Cryptodome.Cipher：包含保护数据机密性的算法，有 3 种加密算法：对称加密、非对称加密和混合加密；
2）Cryptodome.Random：返回长度为 N 的随机字节字符串；
3）Cryptodome.PublicKey：系统定义了一个密钥对，其中一个是机密的(私钥)，另一个是可以公开的（公钥）；
4）Cryptodome.Hash：哈希函数，以任意二进制字符串为输入，生成随机的固定长度输出，又称为消息指纹或哈希值；
5）Cryptodome.Signature：数字签名的算法，用于保证完整性和不可否认性。

⭐️5.2 RSA加密算法设计

💗5.2.1 生成密钥对

使用非对称密码算法时，Bob 首先要随机生成一对密钥，下面代码是 Python 的 RSA 密钥对生成过程，公钥存储在文件Bob_public_key.pem 中，私钥存储在文件 Bob_private_key.pem 中，程序代码如下：

from Cryptodome.PublicKey import RSA
import binascii
key = RSA.generate(2048)
f1= open('Bob_private_key.pem','wb')
f1.write(key.export_key(format='PEM'))
f1.close()
f2=open("Bob_public_key.pem",'wb')
f2.write(key.publickey().export_key(format='PEM'))
f2.close()

💗5.2.2 RSA数据加密

Alice要向Bob发送加密的数据，假设Alice已经获得Bob的公钥，且存储在一个名为Bob_public_key.pem的文件中。因为希望能够加密任意长度的数据，一般使用混合加密方法，即使用 AES 加密消息明文，再用 RSA 加密随机生成的会话密钥，使用 EAX 模式来检测未经授权的修改。过程如下：

from Cryptodome.PublicKey import RSA
from Cryptodome.Random import get_random_bytes
from Cryptodome.Cipher import AES,PKCS1_OAEP
from binascii import b2a_hex
message="……".encode("utf-8")
receiver_key=RSA.import_key(open("Bob_public_key.pem").read())
session_key=get_random_bytes(16)
# 使用 RSA 公钥加密会话密钥
cipher_rsa=PKCS1_OAEP.new(receiver_key)
enc_session_key=cipher_rsa.encrypt(session_key)
# 使用 AES算法及会话密钥加密消息
cipher_aes=AES.new(session_key,AES.MODE_EAX)
ciphertext,tag=cipher_aes.encrypt_and_digest(message)
fo=open("encrypted_message.bin","wb")[fo.write(i)foriin(enc_session_key,cipher_aes.nonce,tag,ciphertext)]
#print(b2a_hex(ciphertext))

💗5.2.3 RSA解密算法

Bob 首先使用自己的私钥解密，获取会话密钥，然后进行密文解密。具体算法如下：

from Cryptodome.PublicKey import RSA
fromCryptodome.Cipher import AES,PKCS1_OAEP
fi=open("encrypted_message.bin","rb")
private_key=RSA.import_key(open("Bob_private_key.pem").read())
enc_session_key,nonce,tag,ciphertext= \
[fi.read(i)foriin(private_key.size_in_bytes(),16,16,-
1)]
# Bob使用私钥解密 AES会话密钥
cipher_rsa=PKCS1_OAEP.new(Bob_private_key.pem)
session_key=cipher_rsa.decrypt(enc_session_key)
# 使用 AES会话密钥解密消息
cipher_aes=AES.new(session_key,AES.MODE_EAX,nonce)
message=cipher_aes.decrypt_and_verify(ciphertext,tag)
print(message.decode("utf-8"))

💗5.2.4 RSA数据签名

发送者 Bob使用自己的私钥对消息进行签名,接收者 Alice使用 Bob的公钥对签名信息和完整性进行解密及真实性验证。

from Cryptodome.Hash import SHA256
from Cryptodome.PublicKey import RSA
from Cryptodome.Signature import pkcs1_15
message = "……".encode("utf-8")
key=RSA.import_key(open('Bob_private_key.pem').read())
h = SHA256.new(message)
signature = pkcs1_15.new(key).sign(h)
#接收者可以使用匹配的公钥来验证接收到的消息的真实性
key=RSA.import _ key(open('Bob_public_key.pem').read())
h = SHA256.new(message)
try:
	pkcs1_15.new(key).verify(h, signature)
	print("The signature is valid.")
except(ValueError, TypeError):
	print("The signature is not valid.")

⭐️5.3 消息内容的AES加密与解密

假设明文为：

Message="On December 3, 1941, chi bu chau deciphered a secret message intercepted by the Japanese foreign ministry to ambassador nomura in the United States:1. Inform the concerned depositor to transfer the deposit to the neutral country bank as far as possible; 2.The imperial government decided to take drastic action."

使用 get_random_bytes(16) 随机生成的加密密钥为：

key=76b2d1bdfa8548c7937a22bfffa2a452

AES算法加密后的密文为：

Encrypt_text="3wz35qGoZe4zY5J6IBPWniTJ9n6m6mkJJdv7ba/uPQMIZh0651yuyZj4BTaBTSA9Dg4HysETKpPDZEqlUaatgmAqczKOJYp5mBviIoL + b + TeiFjXrsi85RYtZXVAruRelql6TiKe2D5A84OkP8AFeD2qmhfKVY + A0oXn5QBS3801mKzqbqxHPVwKFlKqdaUMbEGSoxFJ7SBVxGZmZCIAm5lXhpKIUBl3e3HZzGNGLAfqQC2xBGbrH24MLDwexQJClwqF4yYutStB + fP3T3VsMVdcY191mwKIQzwh/tQkc + itbGUsdEjEzsh1LhyjV4KenOLesyr1ECPHXBrA2hC4MF3sjlm8HEoVH9eQo5xXumX4zCCHxC8uCUCNz8LNhpJ + KyRKGX3PgL0d0dE2y68+0S1vluQEzUCTNf4W5OQQTsM="

同理，接收方首先使用自己的私钥解密并获得对称密钥 key，然后对密文 Encrypt_text 解密获得明文 Message。

🍊🍊🍊

总结不易，看到这那就来个三连吧，肝。。。 🍺🍺🍺

总结不易，看到这那就来个三连吧，肝。。。 🍺🍺🍺

🍊🍊🍊

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐