NumPy 2.x 完全指南【七】根据数值范围创建数组
在 Python3 中我们学过 range 函数,它是一个用于生成整数序列的内置函数,广泛用于循环控制和序列生成。range() 返回的是可迭代 range 对象,不预先生成所有元素,而是需要时才生成下一个数。
文章目录
1. 引言
在 Python3 中我们学过 range 函数,它是一个用于生成整数序列的内置函数,广泛用于循环控制和序列生成。range() 返回的是可迭代 range 对象,不预先生成所有元素,而是需要时才生成下一个数。
基础语法:
range(stop)
range(start, stop)
range(start, stop, step)
参数说明:
start:序列的起始值(默认为 0)。stop:序列的结束值(不包含该值)。step:序列的步长(默认为 1)。
在 NumPy 中提供了更丰富的根据范围生成数组的多种函数:
arangelinspacelogspacegeomspace- 稀疏网格相关(后续介绍):
meshgridmgridogrid
2. 等差数列
2.1 arange
numpy.arange:生成固定步长的等差数列。
函数定义:
arange([start,] stop[, step,], dtype=None, *, device=None, like=None)
注意事项:
- 支持整数和浮点数
- 生成的数组范围为半开区间
[start, stop),即包含start但不包含stop - 使用非整数步长(如
0.1)可能导致结果不稳定 - 返回值类型为
ndarray数组对象
参数说明:
start:起始值,若未指定则默认从0开始。stop:终止值(不包含在结果中)。step:相邻元素的间隔值,默认值为1,若指定step为位置参数,则必须同时指定start。dtype:数据类型,默认根据输入参数自动推断类型。device:指定数组存储设备。like:类数组对象, 允许创建非NumPy数组的参考对象。
示例 1 ,生成简单整数序列:
print(np.arange(5)) # [0 1 2 3 4]
print(np.arange(2, 8, 2)) # [2 4 6]
示例 2 ,生成浮点序列:
print(np.arange(0, 1, 0.3)) # [0.0, 0.3, 0.6, 0.9]
示例 3 ,生成反向序列:
print(np.arange(5, 1, -1)) # [5 4 3 2]
2.2 linspace
numpy.linspace:生成固定数量的等差数列。
函数定义:
def linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None,
axis=0, *, device=None):
参数说明:
start:序列起始值。stop:序列结束值。num:生成的样本数(默认 50)。endpoint:是否包含stop(默认 True)。retstep:是否返回步长(默认False)。dtype:输出数组的数据类型(默认None,自动推断)。axis:当start或stop是数组时,决定生成的样本在结果数组中的轴位置。默认值为 0,即在数组的最前面插入新维度;若设为 -1,则在最后面插入。device:指定数组存储设备。
和 numpy.arange 的主要区别:
| 特性 | numpy.linspace |
numpy.arange |
|---|---|---|
| 核心参数 | 起点、终点、样本数量(num) |
起点、终点、步长(step) |
| 终点是否包含 | 默认包含(可通过 endpoint=False 排除) |
默认不包含(类似 Python 的 range) |
| 数据生成逻辑 | 根据样本数量等分区间 | 根据步长逐步累加 |
| 浮点数精度 | 更稳定(避免步长累加的浮点误差) | 可能因步长累加导致终点不精确 |
示例 1 ,通过 num 参数控制生成的样本数量,生成包含终点的简单序列:
import numpy as np
# 生成 0 到 10 之间的 5 个等间隔数(包含终点)
arr = np.linspace(0, 10, 5)
print(arr) # 输出: [ 0. 2.5 5. 7.5 10. ]
示例 2 ,不包含终点并返回步长:
# 生成 0 到 10 之间的 5 个数(不包含终点),并返回步长
arr, step = np.linspace(0, 10, 5, endpoint=False, retstep=True)
print(arr) # 输出: [0. 2. 4. 6. 8.]
print(step) # 输出: 2.0
示例 3 ,起始值为一维数组:
start = np.array([1, 2, 3])
print(start.shape) # 输出: (3,)
print(start) # 输出: [1 2 3]
# 结束值
stop = 10
# 样本数量
num = 5
起始值为数组时,生成的结果数组会增加一个维度(轴),而参数 axis 就是控制结果数组中样本的轴方向。例如,上面起始值为一维数组时,会生成二维数组,可以选择在 0 轴或者 1 轴的方向上进行生成: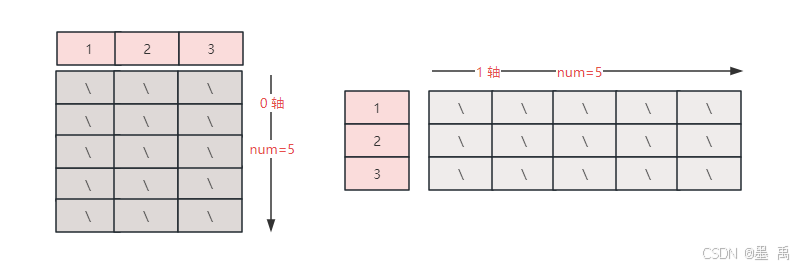
axis 的默认值为 0 ,表示始终选择在结果数组的第一个轴上进行生成,示例:
result_axis0 = np.linspace(start, stop, num)
print(result_axis0.shape) # 输出: (5, 3)
print(result_axis0)
# 输出
# [[ 1. 2. 3. ]
# [ 3.25 4. 4.75]
# [ 5.5 6. 6.5 ]
# [ 7.75 8. 8.25]
# [10. 10. 10. ]]
axis 为 -1 ,表示始终选择在结果数组的最后一个轴上进行生成,示例:
result_axis_1 = np.linspace(start, stop, num, axis=-1)
print( result_axis_1.shape) # 输出: (3, 5)
print(result_axis_1)
# 输出:
#[[ 1. 3.25 5.5 7.75 10. ]
# [ 2. 4. 6. 8. 10. ]
# [ 3. 4.75 6.5 8.25 10. ]]
如果是二维或者更高维度的数组,同理进行类推即可,比如 start 参数是形状为(2,3,4)的三维数组,其结果为一个四维数组,新维度的长度等于样本数 num(示例中是 5 ) ,这样可以在(2,3,4)的任意位置插入新轴,示例:
axis = 0时:(5,2,3,4)axis = 1时:(2,5,3,4)axis = 2时:(2,3,5,4)axis = -1时:(2,3,4,5)
3. 等比数列
3.1 前置知识
3.1.1 等比数列
等比数列列是指从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列,这个常数叫做等比数列的公比。
形式为:
a i = a 1 ⋅ r ( i − 1 ) a_i = a_1 \cdot r^{(i-1)} ai=a1⋅r(i−1)
其中:
- i i i:项数(第几项,从
1开始) - a 1 a_1 a1:首项
- a i a_i ai:第 i i i项
- r r r:公比
3.1.2 对数
对数(Logarithm)是指数的逆运算,用于求解底数的多少次幂等于某个数。
基本公式:若 a b = N a^b = N ab=N(其中 a > 0 a > 0 a>0 且 a ≠ 1 a \neq 1 a=1),则:
log a N = b \log_a N = b logaN=b
其中:
- a a a 称为底数
- N N N 称为真数
- b b b 称为以 a a a 为底 N N N 的对数
一个简单示例:
- 指数形式: 2 3 = 8 2^3 = 8 23=8
- 对数形式: log 2 8 = 3 \log_2 8 = 3 log28=3
- 解读:底数 2 2 2 的 3 3 3 次幂等于真数 8 8 8
3.1.3 对数函数
对数函数(Logarithmic Function)是以真数(N)为自变量,对数(b)为因变量,底数(a)为常量的函数,是六类基本初等函数之一。
基本公式:
y = log a ( x ) y = \log_a(x) y=loga(x)
其中:
- a a a 是对数的底数( a > 0 a > 0 a>0 且 a ≠ 1 a \neq 1 a=1)。
- x x x 是函数的输入值( x > 0 x > 0 x>0)。
- y y y 是输出值,表示 a a a 的多少次幂等于 x x x,即 a y = x a^y = x ay=x。
- 底数 a > 1 a>1 a>1 时:函数递增,适合描述增长速率逐渐放缓的场景。
- 底数 0 < a < 1 0<a<1 0<a<1 时:函数递减,适合描述衰减速率逐渐加快的场景。

3.1.4 对数刻度
基础概念:
- 线性刻度(
Linear Scale):坐标轴上的刻度按等距数值均匀分布,数值变化为加法增长。 - 对数刻度(
Logarithmic Scale):将数据按对数值(而非原始值)分布的坐标轴表示方法。
线性刻度之间的间隔相等,比如普通直尺上的厘米刻度。但是线性刻度能容纳的数值有限,所以引入了对数刻度,当数据的值在一个很大范围内时,利用对数使此降低到一个更加易处理的范围。
示例,有一个以 10 为底的对数刻度,每个刻度值都定义为 10 的对数,每个刻度对应的实际值为 1 0 0 , 1 0 1 , 1 0 2 , … 10^0, 10^1, 10^2, \dots 100,101,102,… :
3.2 logspace
numpy.logspace:生成在对数刻度上均匀分布的数值序列。指数部分是一个等差数列,数值部分是一个等比数列。
函数定义:
def logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None,
axis=0):
参数说明:
start:对数刻度上的起始值,实际起始值为base^start,例如,base=10、start=2时对应实际值是100。stop:对数刻度上的结束值,实际结束值为base^stop。base:对应对数函数中的底数,默认值为10.0。num:生成的样本数量,默认值为50。endpoint:是否包含实际终止值,默认值为True。dtype:数据类型,自动推断为浮点型。axis:在输入数组时,指定结果插入轴的位置。
示例 1 :
import numpy as np
arr = np.logspace(1, 3, num=5)
print(arr) # 输出: [ 10. 31.62 100. 316.23 1000. ]
结果分析,首先参数如下:
start:1stop:3num:5base:10(默认值)
在对数刻度上的范围为 [start,stop] 即 [1,3],如果要生成 5 (num)个均匀样本的话(等差数列),很容易计算出来步长为 0.5 ,那么所有样本在对数刻度上的值为 (1,1.5,2,2.5,3),再转换为实际值,即:
| 指数表达式 | 计算结果(保留两位小数) |
|---|---|
| 1 0 1 10^1 101 | 10.00 |
| 1 0 1.5 10^{1.5} 101.5 | ≈ ≈ ≈ 31.62 |
| 1 0 2 10^2 102 | 100.00 |
| 1 0 2.5 10^{2.5} 102.5 | ≈ ≈ ≈ 316.23 |
| 1 0 3 10^3 103 | 1000.00 |
在默认情况下(endpoint=True)可以直接套用公式:
a i = base ( start + i ⋅ stop − start n − 1 ) a_i = \text{base}^{\left( \text{start} + i \cdot \frac{\text{stop} - \text{start}}{n-1} \right)} ai=base(start+i⋅n−1stop−start)
其中:
i:当前元素索引(从0到n-1)。ai:索引为i的元素。base:底数(默认为10)。start:底数的起始指数stop:底数的结束指数n:生成的元素总数(num参数)。
当 endpoint=False 时:
a i = base ( start + i ⋅ stop − start n ) a_i = \text{base}^{\left( \text{start} + i \cdot \frac{\text{stop} - \text{start}}{\text{n}} \right)} ai=base(start+i⋅nstop−start)
3.3 geomspace
numpy.geomspace:直接使用实际的数值的范围生成一个等比数列。
函数定义:
numpy.geomspace(start, stop, num=50, endpoint=True, dtype=None, axis=0)
参数说明:
start:起始值,若为数组,结果将沿指定轴扩展维度。stop:终止值。num:生成样本的数量。endpoint:是否包含终止值,默认True。dtype: 数据类型。axis:仅当start或stop为类数组时有效,默认在首部插入新轴。
和 numpy.logspace 核心区别:
| 特性 | numpy.geomspace |
numpy.logspace |
|---|---|---|
| 参数意义 | 直接指定数值范围(如 1 到 1000) |
指定底数的指数范围(如 0 到 3 对应 10^0=1 到 10^3=1000) |
| 默认底数 | 无固定底数,由 start/stop 决定 |
默认底数为 10,可自定义(base 参数) |
| 设计目的 | 直接生成任意数值范围的等比数列 | 生成以固定底数为基的指数序列(如科学计算中的分贝、频率) |
| 等价关系 | 当 s t a r t = b a s e a start=base^a start=basea, s t o p = b a s e b stop=base^b stop=baseb 时,与 logspace(a, b, base=base) 等价 |
本质是 geomspace 的固定底数特例 |
假设生成 num 个数的等比数列,末项为 a n = stop a_n = \text{stop} an=stop,根据等比数列公式 a i = a 1 ⋅ r ( i − 1 ) a_i = a_1 \cdot r^{(i-1)} ai=a1⋅r(i−1) ,则:
a n = a 1 ⋅ r ( n − 1 ) a_n = a_1 \cdot r^{(n-1)} an=a1⋅r(n−1)
代入 a 1 = start a_1 = \text{start} a1=start, a n = stop a_n = \text{stop} an=stop,解得公比 r r r:
r = ( stop start ) 1 n − 1 r = \left( \frac{\text{stop}}{\text{start}} \right)^{\frac{1}{n-1}} r=(startstop)n−11
示例 1 中的求公比结果为 10 :
r = ( stop start ) 1 n u m − 1 = ( 1000 1 ) 1 4 − 1 = 100 0 1 3 = 1000 3 = 10 r = \left( \frac{\text{stop}}{\text{start}} \right)^{\frac{1}{num-1}}= \left( \frac{\text{1000}}{\text{1}} \right)^{\frac{1}{4-1}}=1000^{\frac{1}{3}}= \sqrt[3]{1000} =10 r=(startstop)num−11=(11000)4−11=100031=31000=10
最后按公比 r r r 逐项生成:
arr = [ start , start ⋅ r , start ⋅ r 2 , … , start ⋅ r ( n − 1 ) ] \text{arr} = \left[ \text{start}, \ \text{start} \cdot r, \ \text{start} \cdot r^2, \ \dots, \ \text{start} \cdot r^{(n-1)} \right] arr=[start, start⋅r, start⋅r2, …, start⋅r(n−1)]
示例 1 ,在 1 到 1000 的区间内生成 4 个等比数:
g1 = np.geomspace(1, 1000, num=4)
print(g1) # [ 1. 10. 100. 1000.]
不包含结束值(endpoint=False)时,等比的计算公式为:
r = ( stop start ) 1 n u m r = \left( \frac{\text{stop}}{\text{start}} \right)^{\frac{1}{num}} r=(startstop)num1
示例 2 中的求公比结果为 5.623 :
r = ( 1000 1 ) 1 4 = 100 0 0.25 = ( 1 0 3 ) 0.25 = 1 0 0.75 ≈ 5.623 r = \left( \frac{1000}{1} \right)^{\frac{1}{4}} = 1000^{0.25} = (10^3)^{0.25} = 10^{0.75} \approx 5.623 r=(11000)41=10000.25=(103)0.25=100.75≈5.623
示例 2 ,不包含终止值,生成 4 个数:
g1 = np.geomspace(1, 1000, num=4, endpoint=False)
print(g1) # [ 1. 5.62341325 31.6227766 177.827941 ]

GitCode 天启AI是一款由 GitCode 团队打造的智能助手,基于先进的LLM(大语言模型)与多智能体 Agent 技术构建,致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话,还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力,真正做到“一句话,让 Al帮你完成复杂任务”。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容









所有评论(0)