1. 题目

2. 读题（需要重点注意的东西）

读题：
身高的排列如下：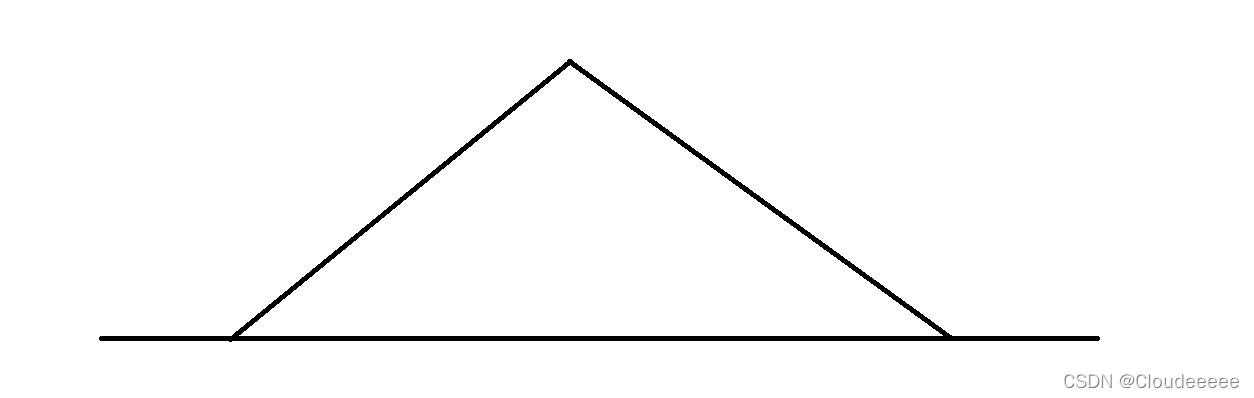

问：计算最少需要几位同学出列 ===》 最多有多少同学可以构成合唱队形，即求正反向的最长上升子序列之和！

思路：
具体思路与[AcWing] 1014. 登山（C++实现）最长上升子序列模型、求正反向最长上升子序列之和相同，在此不再赘述。

3. 解法

---------------------------------------------------解法---------------------------------------------------

#include<iostream>
using namespace std;

const int N = 110;
int n;
int h[N];
int f[N],g[N];

int main(){
    cin >> n;
    for(int i = 1;i <= n; i++) cin >> h[i];
    
    for(int i = 1;i <= n;i++){
        f[i] = 1;
        for(int j = 1;j <= i;j++)
            if(h[j] < h[i]) f[i] = max(f[i],f[j]+1);
    }
    
    for(int i = n;i >= 1;i--){
        g[i] = 1;
        for(int j = n;j >= 1;j--)
            if(h[j] < h[i]) g[i] = max(g[i],g[j]+1);
    }
    
    int res = 0;
    for(int i = 1;i <= n;i++) res = max(res,f[i]+g[i]-1);
    
    cout << n - res; // 与题 AcWing 1014. 登山唯一不同之处，上面都是相同的
    
    return 0;
}

可能存在的问题

4. 可能有帮助的前置习题

• [AcWing] 1014. 登山（C++实现）最长上升子序列模型、求正反向最长上升子序列之和

5. 所用到的数据结构与算法思想

• 动态规划
• 最长上升子序列问题

6. 总结

最长上升子序列模型，可以发展为不同的最长上升子序列题目

最长上升子序列模型的特征：
1. 以每个点为终点都要判断一遍
2. 路径为一条上升子序列（或下降子序列）
3. 要求的数列会呈如下分布：