概述

DPP（Determinantal Point Processes）算法是一种用于建模和选择具有多样性的子集的概率模型。DPP是通过行列式来度量子集之间的多样性，它广泛应用于机器学习、信息检索、推荐系统、自然语言处理等领域，尤其适用于需要同时考虑相关性和多样性的场景。

超平行体

在介绍DPP算法原理之前，先了解下超平行体的概念。

基本概念

超平行体是平行体的高维推广。为了理解这一概念，我们可以从较低维度开始：

• 平行体（Parallelotope）：在二维和三维空间中，平行体可以理解为平行四边形（二维）或平行六面体（即长方体，三维）。平行体是由多个平行的面所构成的多面体，其中每个面的形状是相同的，且所有的边都是平行的。

• 超平行体：当我们将这个概念扩展到更高维度时，超平行体就是一个高维空间中的几何形状，它的每个面（或“超面”）是与其他面平行的。具体地，超平行体是一个n-维凸多面体，包含了一系列平行的平面（或超平面）构成的面，每个面是一个低维的平行体。

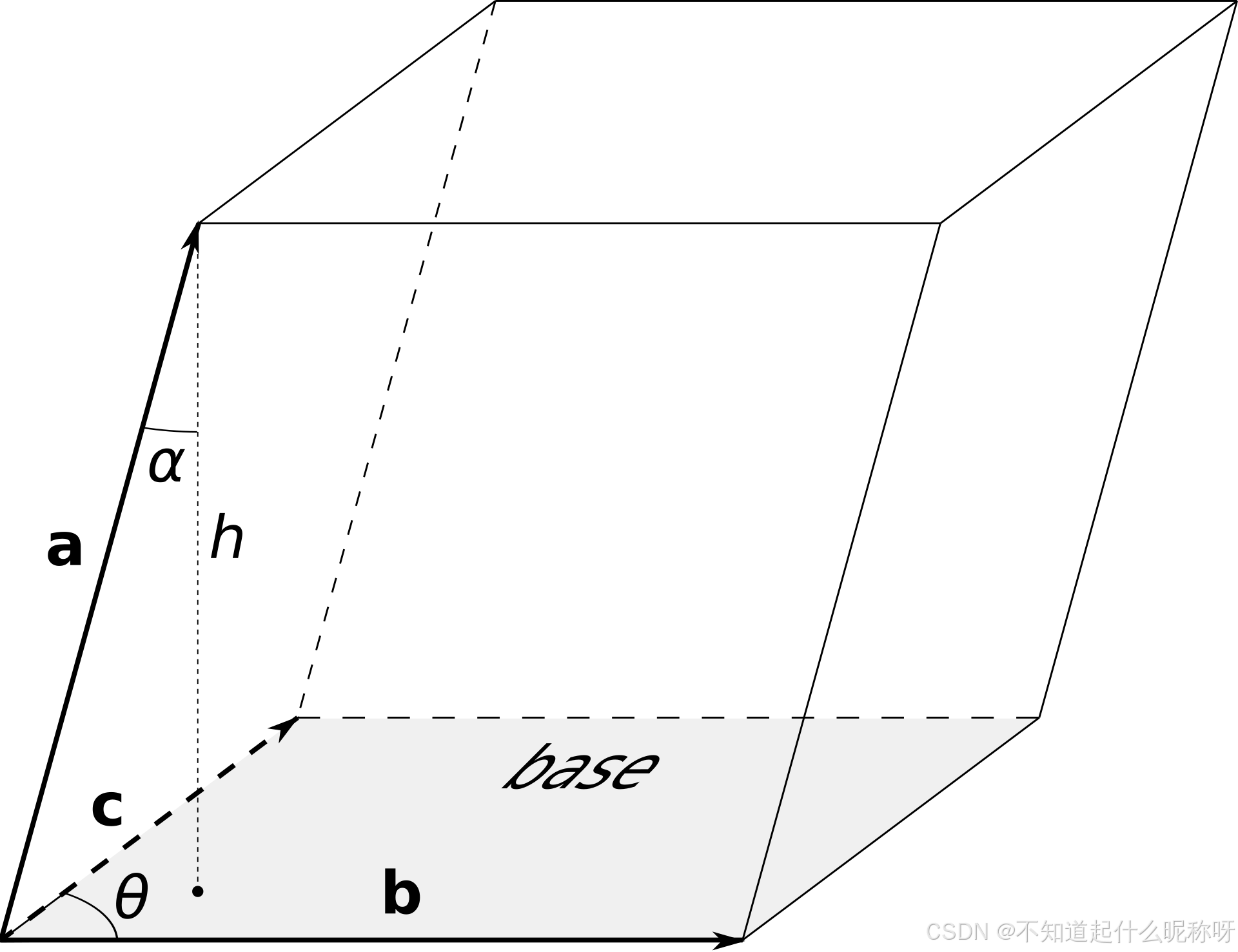
平行六面体就是一个三维的平行体，通过向量a、b、c可以确定平行六面体的形状。

假设有一组向量可以确定一个K维超平行体，这个平行体中的任意一个点都可以通过这K个向量表示。

但是要求，因为d维的空间中只会有小于等于d维的超平行体，2维空间中是不存在三维超平行体的。

想要超平行体有意义，这K个向量必须线性无关。以上面的平行六面体为例，如果a、b、c之间线性相关，即存在一个向量可以用另外两个向量表示，这时三维的平行六面体就变成了二维的平行四边形。

超平行体和行列式的关系

下面再来看一下超平行体体积和行列式的关系。

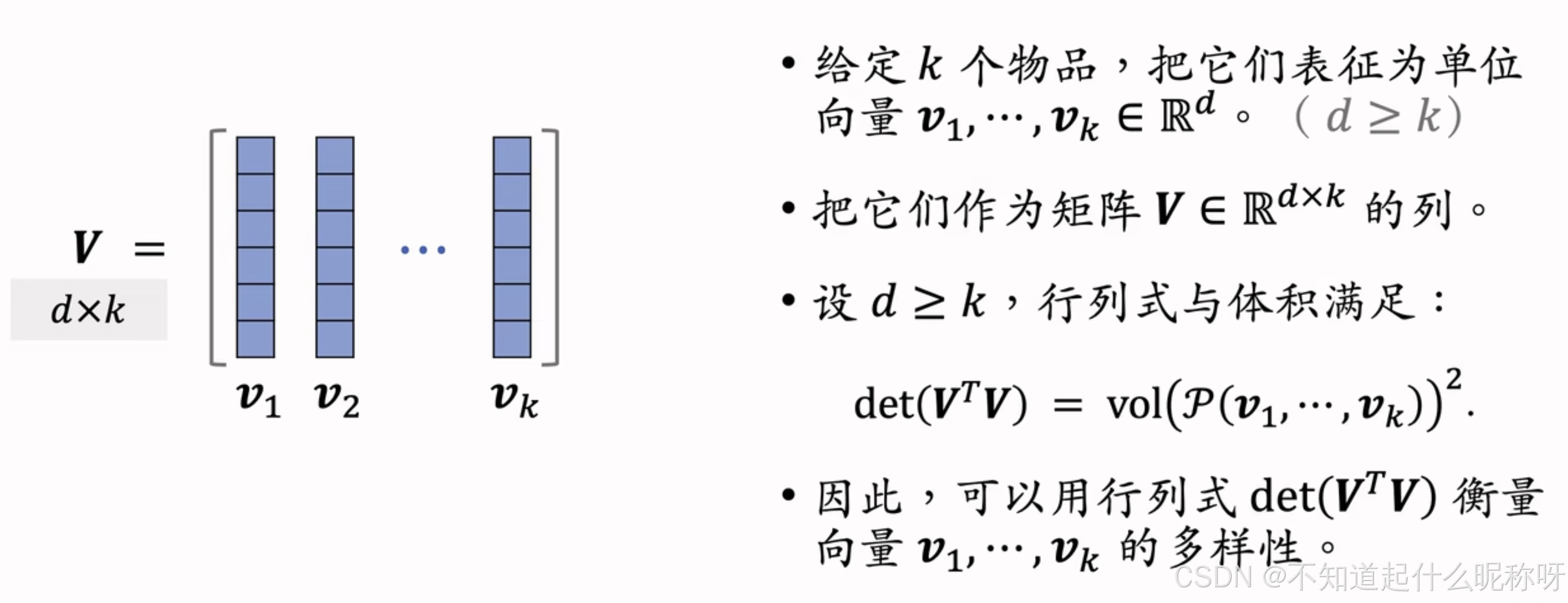
• k维的超平行体如果存在线性相关的向量，就会退化为k-1维或者更低维的子空间上，这时我们统一定义为超平行体的体积为0，而不再继续研究子空间的超平行体的体积。
• 当两两正交时，此时体积最大，等于每个向量模的乘积。
• 当线性无关时，此时体积最小，为0。

DPP算法原理

回顾之前的一篇文章推荐系统混排 - MMR多样性算法-CSDN博客，MMR算法的思路就是在多样性和相关性之间做balance，DPP算法的思路也是一致的，只不过这里的多样性衡量方式有变化。

初版算法

Hulu的论文将DPP算法应用到推荐系统：

这个公式的含义是从集合中找出个物品，要求这个物品的融合分 + 行列式最大，融合分保证相关性，行列式的值保证多样性。

下面来分析下这个时间复杂度，设集合中的个数为，每一个物品向量的维度都是：

• 计算就是计算向量两两之间的相似度，时间复杂度是；
• 计算行列式的值，事件复杂度是；

最终的时间复杂度就是，这个复杂度太高了，推荐系统留给多样性的时间只有几ms，无法求解。

算法改进一

改进的思想是贪心，每次都从集合中选择多样性分+融合分最高的物品，和MMR算法的逻辑是一致的。

问题在于改进后的算法时间复杂度仍然非常高，实际工程中也不会这么用。

算法改进二

这种改进方法的核心是利用Cholesky分解将矩阵A分解为一个下三角矩阵及其转置矩阵乘积的形式。这样做的好处是方便计算行列式，下三角矩阵的行列式等于对角线元素的乘积。

这种改进算法的时间复杂度为。

 滑动窗口

DPP和MMR这种贪心算法都存在一个问题，就是随着集合中内容越来越多，集合中的物品和集合中的物品基本都相似，这样算法就退化成了按照融合分选择的下一个物品了。

在推荐系统中，一般只会要求相近的资源多样性较好即可，没必要要求第一个和第100个资源也不相似。所以设计滑动窗口，可以有效解决算法失效的问题。

参考

重排04：DPP 多样性算法（上）_哔哩哔哩_bilibili

重排05：DPP 多样性算法（下）_哔哩哔哩_bilibili