第5章 决策树

1．分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if-then规则的集合，也可以看作是定义在特征空间划分上的类的条件概率分布。

2．决策树学习旨在构建一个与训练数据拟合很好，并且复杂度小的决策树。因为从可能的决策树中直接选取最优决策树是NP完全问题。现实中采用启发式方法学习次优的决策树。

决策树学习算法包括3部分：特征选择、树的生成和树的剪枝。常用的算法有ID3、C4.5和CART。

3．特征选择的目的在于选取对训练数据能够分类的特征。特征选择的关键是其准则。常用的准则如下：

（1）样本集合$D$对特征$A$的信息增益（ID3）

$$g(D,A)=H(D)-H(D|A)$$

$$H(D)=-\sum _{k=1}^K\frac{\left|C_k\right|}{|D|}{\log }_2\frac{\left|C_k\right|}{|D|}$$

$$H(D|A)=\sum _{i=1}^n\frac{\left|D_i\right|}{|D|}H\left(D_i\right)$$

其中，$H(D)$是数据集$D$的熵，$H(D_i)$是数据集$D_i$的熵，$H(D|A)$是数据集$D$对特征$A$的条件熵。 $D_i$是$D$中特征$A$取第$i$个值的样本子集，$C_k$是$D$中属于第$k$类的样本子集。$n$是特征$A$取 值的个数，$K$是类的个数。

（2）样本集合$D$对特征$A$的信息增益比（C4.5）

$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$

其中，$g(D,A)$是信息增益，$H(D)$是数据集$D$的熵。

（3）样本集合$D$的基尼指数（CART）

$$\mathrm{Gini}(D)=1-\sum _{k=1}^K{\left(\frac{\left|C_k\right|}{|D|}\right)}^2$$
特征$A$条件下集合$D$的基尼指数：

$$\mathrm{Gini}(D,A)=\frac{\left|D_1\right|}{|D|}\mathrm{Gini}\left(D_1\right)+\frac{\left|D_2\right|}{|D|}\mathrm{Gini}\left(D_2\right)$$
4．决策树的生成。通常使用信息增益最大、信息增益比最大或基尼指数最小作为特征选择的准则。决策树的生成往往通过计算信息增益或其他指标，从根结点开始，递归地产生决策树。这相当于用信息增益或其他准则不断地选取局部最优的特征，或将训练集分割为能够基本正确分类的子集。

5．决策树的剪枝。由于生成的决策树存在过拟合问题，需要对它进行剪枝，以简化学到的决策树。决策树的剪枝，往往从已生成的树上剪掉一些叶结点或叶结点以上的子树，并将其父结点或根结点作为新的叶结点，从而简化生成的决策树。

这里也感谢DataWhale的无私奉献，我结合了原先的学习资料，整合了一下，得到现有的笔记，这里也欢迎大家参与DataWhale的组队学习中，https://datawhalechina.github.io/statistical-learning-method-solutions-manual/#/

特征选择

熵

$$H(p)=H(X)=-\sum _{i=1}^n{p}_i\log p_i$$

• 熵只与X的分布有关，与X取值无关
• 定义0log0=0，熵是非负的
• 表示随机变量不确定性的度量
• 对数以2为底或以e为底(自然对数)，这时单位分别为比特(bit)或纳特(nat)，相差一个系数
• $0\le H(p)\le \log n$

条件熵

• 随机变量$(X,Y)$的联合概率分布为

$$P(X=x_i,Y=y_j)=p_{ij},i=1,2,\dots ,n;j=1,2,\dots ,m$$

• 条件熵$H(Y|X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性

$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$

其中$p_i=P(X=x_i),i=1,2,\dots ,n$

当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时，所对应的熵与条件熵分别称为经验熵和经验条件熵

信息增益

• 特征$A$对训练数据集$D$的信息增益$g(D|A)$，定义为集合$D$的经验熵$H(D)$与特征$A$给定的条件下$D$的经验条件熵$H(D|A)$之差

$$g(D,A)=H(D)-H(D|A)$$

• 熵$H(Y)$与条件熵$H(Y|X)$的差称为互信息(mutual information)

• 决策树中的信息增益等价于训练数据集中的类与特征的互信息

• 考虑ID这种特征， 本身是唯一的。按照ID做划分， 得到的经验条件熵为0, 会得到最大的信息增益。所以， 按照信息增益的准则来选择特征， 可能会倾向于取值比较多的特征

信息增益比

• 使用信息增益比可以对上面倾向取值较多的特征的问题进行校正，这时特征选择的另一准则

$$\begin{gathered} g_R(D,A)=\frac{g(D,A)}{H_A(D)} \\ {H}_A(D)=-\sum _{i=1}^n\frac{D_i}{D}lo{g}_2\frac{D_i}{D} \end{gathered}$$

其中，$H_A(D)=-{\sum }_{i=1}^n\frac{|D_i|}{|D|}{\log }_2\frac{|D_i|}{|D|}$，n是特征取值的个数。

决策树的生成

ID3算法

输入：训练数据集$D$, 特征集$A$，阈值$ϵ$
输出：决策树$T$

1. 如果$D$中所有实例属于同一类$C_k$，则$T$为单节点树，并将类$C_k$作为该节点的类标记，返回$T$
2. 如果$A$是空集，则$T$为单节点树，并将实例数最多的类作为该节点类标记，返回$T$
3. 计算$g$, 选择信息增益最大的特征$A_g$
4. 如果$A_g$的信息增益小于$ϵ$，则置$T$为单节点树，$D$中实例数最大的类$C_k$作为类标记，返回$T$
5. 否则，依$A_g=a_i$将D划分若干非空子集$D_i$，$D_i$中实例数最大的类$C_k$作为类标记，构建子结点，由结点及其子结点 构成树$T$，返回$T$
6. $D_i$训练集，$A-A_g$为特征集，递归调用前面步骤，得到$T_i$，返回$T_i$

不过对于ID3算法来说，只有树的生成，所以该算法生成的树容易产生过拟合。

利用ID3算法，可以构建例5.1的树

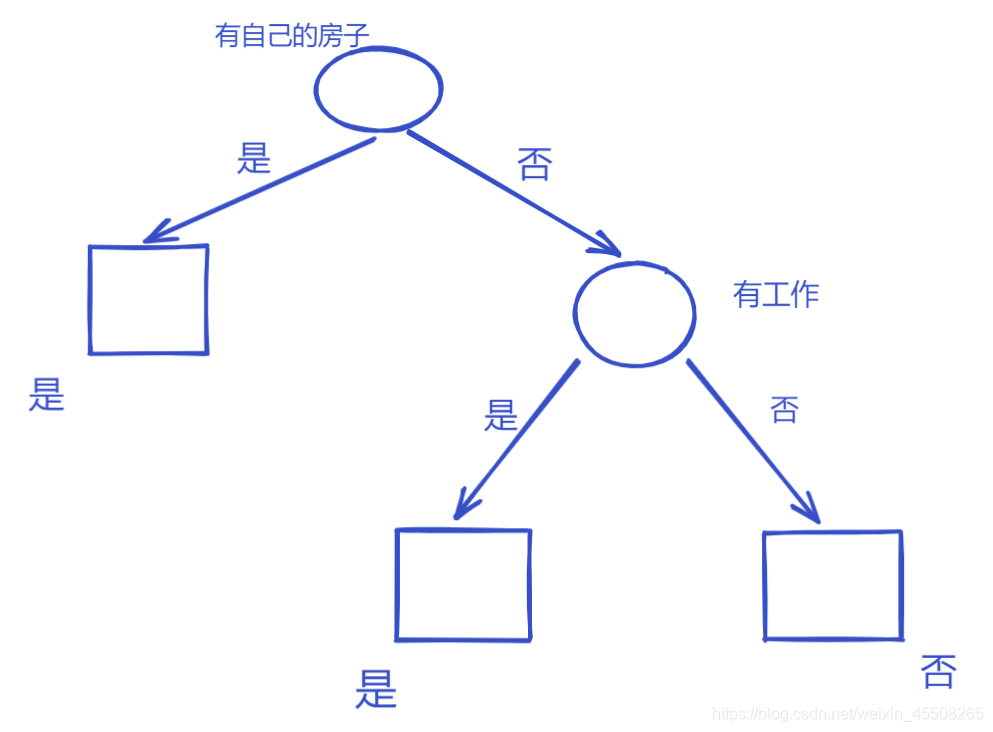
C4.5的生成算法

• 与ID3相似，改用信息增益比来选择特征

输入：训练数据集$D$, 特征集$A$，阈值$ϵ$
输出：决策树$T$

1. 如果$D$属于同一类$C_k$，$T$为单节点树，类$C_k$作为该节点的类标记，返回$T$
2. 如果$A$是空集, 置$T$为单节点树，实例数最多的作为该节点类标记，返回$T$
3. 计算$g$, 选择信息增益比最大的特征$A_g$
4. 如果$A_g$的信息增益比小于$ϵ$，$T$为单节点树，$D$中实例数最大的类$C_k$作为类标记，返回$T$
5. 否则，依$A_g=a_i$将D划分若干非空子集$D_i$，$D_i$中实例数最大的类$C_k$作为类标记，构建子结点，由结点及其子结点 构成树$T$，返回$T$
6. $D_i$训练集，$A-A_g$为特征集，递归调用前面步骤，得到$T_i$，返回$T_i$

• ID3和C4.5在生成上，差异只在准则的差异

决策树的剪枝

树的剪枝

• 决策树的剪枝往往通过极小化决策树整体的损失函数或代价函数来实现的
• 树$T$的叶结点个数为$|T|$，$t$是树$T$的叶结点，该结点有$N_t$个样本点，其中$k$类的样本点有$N_{tk}$个，$H_t(T)$为叶结点$t$上的经验熵， $\alpha ⩾0$为参数，决策树学习的损失函数可以定义为

$$C_{\alpha }(T)=\sum _{i=1}^{|T|}{N}_t{H}_t(T)+\alpha |T|$$

其中
$$H_t(T)=-\sum _k\frac{N_{tk}}{N_t}\log \frac{N_{tk}}{N_t}$$

$$C(T)=\sum _{t=1}^{|T|}{N}_t{H}_t(T)=-\sum _{t=1}^{|T|}\sum _{k=1}^K{N}_{tk}\log \frac{N_{tk}}{N_t}$$

这时有
$$C_{\alpha }(T)=C(T)+\alpha |T|$$
其中$C(T)$表示模型对训练数据的误差，$|T|$表示模型复杂度，参数$\alpha ⩾0$控制两者之间的影响

• 较大的$\alpha$促使选择较简单的模型（树）
• 较小的$\alpha$促使选择较复杂的模型（树）
• $\alpha =0$以为只考虑模型与训练的拟合程度，不考虑模型的复杂度

剪枝算法

输入：生成算法生成的整个树$T$，参数$\alpha$

输出：修剪后的子树$T_{\alpha }$

1. 计算每个结点的经验熵
2. 递归地从树的叶结点向上回缩
   假设一组叶结点回缩到其父结点之前与之后的整体树分别是$T_B$和$T_A$，其对应的损失函数分别是$C_{\alpha }(T_A)$和$C_{\alpha }(T_B)$，如果$C_{\alpha }(T_A)⩽C_{\alpha }(T_B)$则进行剪枝，即将父结点变为新的叶结点
3. 返回2，直至不能继续为止，得到损失函数最小的子树$T_{\alpha }$

• 决策树的剪枝算法可以由一种动态规划的算法实现

CART

• 决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则，对分类树用基尼系数最小化准则，并进行特征选择，生成二叉树

最小二乘回归树生成算法

• 在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上地输出值，构建二叉决策树

输入：训练数据集$D$
输出：回归树$f(x)$
步骤：

（1）遍历变量$j$，对固定的切分变量$j$扫描切分点$s$，得到满足下面式子的$(j,s)$
$$\underset{j,s}{\min }\left[\underset{c_1}{\min }\sum _{x_i\in R_1(j,s)}(y_i-c_1{)}^2+\underset{c_2}{\min }\sum _{x_i\in R_2(j,s)}(y_i-c_2{)}^2\right]$$
（2）用选定的$(j,s)$, 划分区域并决定相应的输出值
R 1 ( j , s ) = { x ∣ x ( j ) ≤ s } , R 2 ( j , s ) = { x ∣ x ( j ) > s } c ^ m = 1 N ∑ x i ∈ R m ( j , s ) y j , x ∈ R m , m = 1 , 2 R_1(j,s)=\{x|x^{(j)}\leq s\}, R_2(j,s)=\{x|x^{(j)}> s\} \\ \hat{c}_m= \frac{1}{N}\sum\limits_{x_i\in R_m(j,s)} y_j, x\in R_m, m=1,2 R1​(j,s)={x∣x(j)≤s},R2​(j,s)={x∣x(j)>s}c^m​=N1​xi​∈Rm​(j,s)∑​yj​,x∈Rm​,m=1,2
（3）对两个子区域调用(1)(2)步骤， 直至满足停止条件

（4）将输入空间划分为$M$个区域$R_1,R_2,\dots ,R_M$，生成决策树：
$$f(x)=\sum _{m=1}^M{\hat{c}}_{m}I(x\in R_m)$$

CART分类树的生成

• 分类树用基尼指数选择最优特征，同时决定该特征的最优二值切分点

• 概率分布的基尼指数定义

$$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$

• 如果样本集合$D$根据特征$A$是否取某一可能值$a$被分割成$D_1$和$D_2$两部分，则在特征$A$的条件下，集合$D$的基尼指数定义为
  $$Gini(D,A)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$$

输入：训练数据集$D$，停止计算的条件
输出：CART决策树
根据训练数据集，从根节点开始，递归地对每个结点进行以下操作，构建二叉决策树：

1. 设结点地训练数据集为$D$，计算现有特征对该数据集的基尼指数。此时，对每一个特征$A$，对其可能取得每个值$a$，根据样本点对$A=a$的测试为“是”或“否”将$D$分成$D_1$和$D_2$两部分，计算$A=a$时的基尼指数
2. 在所有可能的特征$A$以及它们所有可能的切分点$a$中，选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点。依照最优特征和最优切分点，从现结点生成两个子结点，将训练数据集依特征分配到两个子结点中去。
3. 对两个子结点递归地调用1、2，直至满足停止条件
4. 生成CART决策树

• 算法停止计算的条件是结点中的样本个数小于预定阈值，或样本集的基尼指数小于指定阈值，或者没有更多特征

例5.1

根据书上的例题5.1，用决策树实现

def create_data():
    datasets = [['青年', '否', '否', '一般', '否'],
               ['青年', '否', '否', '好', '否'],
               ['青年', '是', '否', '好', '是'],
               ['青年', '是', '是', '一般', '是'],
               ['青年', '否', '否', '一般', '否'],
               ['中年', '否', '否', '一般', '否'],
               ['中年', '否', '否', '好', '否'],
               ['中年', '是', '是', '好', '是'],
               ['中年', '否', '是', '非常好', '是'],
               ['中年', '否', '是', '非常好', '是'],
               ['老年', '否', '是', '非常好', '是'],
               ['老年', '否', '是', '好', '是'],
               ['老年', '是', '否', '好', '是'],
               ['老年', '是', '否', '非常好', '是'],
               ['老年', '否', '否', '一般', '否'],
               ]
    labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
    # 返回数据集和每个维度的名称
    return datasets, labels

datasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)

# 经验熵
def entropy(datasets):
    data_length = len(datasets)
    label_count = {}
    for i in range(data_length):
        label = datasets[i][-1]
        if label not in label_count:
            label_count[label] = 0
        label_count[label]+=1
    ent = -sum([( p/data_length) * log(p/data_length,2)
                for p in label_count.values()])
    return ent

# 经验条件熵
def condition_entropy(datasets,axis = 0):
    data_length = len(datasets)
    feature_sets = {}
    for i in range(data_length):
        feature = datasets[i][axis]
        if feature not in feature_sets:
            feature_sets[feature] = []
        feature_sets[feature].append(datasets[i])
    condi_ent = sum([ (len(p) / data_length)*entropy(p) for p in feature_sets.values()])
    #print(feature_sets)
    return condi_ent

# 信息增益
def info_gain(ent,condi_entropy):
    return ent - condi_entropy

def info_gain_train(data_sets):
    count = len(datasets[0]) - 1
    ent = entropy(datasets)
    best_feature = []
    for c in range(count):
        c_info_gain = info_gain(ent,condition_entropy(datasets,axis=c))
        best_feature.append((c,c_info_gain))
        print("特征（{}）的信息增益为： {:.3f}".format(labels[c],c_info_gain))
    best = max(best_feature, key=lambda x:x[-1])
    print( '特征({})的信息增益最大，选择为根节点特征'.format(labels[best[0]]))

info_gain_train(datasets)

特征(年龄) - info_gain - 0.083
特征(有工作) - info_gain - 0.324
特征(有自己的房子) - info_gain - 0.420
特征(信贷情况) - info_gain - 0.363
特征(有自己的房子)的信息增益最大，选择为根节点特征

例5.3

利用ID3算法生成决策树

# 定义节点类 二叉树
class Node:
    def __init__(self,root=True,label=None,feature_name = None, feature = None):
        self.root = root
        self.label = label
        self.feature_name = feature_name
        self.feature = feature
        self.tree = {}
        self.result = {'label:':self.label,'feature':self.feature,'tree':self.tree}

    def __repr__(self):
        return '{}'.format(self.result)

    def add_node(self,val,node):
        self.tree[val] = node

    def predict(self,features):
        if self.root is True:
            return self.label
        return self.tree[features[self.feature]].predict(features)

class DTree:
    def __init__(self,epsilon=0.1):
        self.epsilon = epsilon
        self._tree = {}

    # 经验熵
    @staticmethod   #静态方法可以不实例化调用
    def entropy(datasets):
        data_length = len(datasets)
        label_count = {}
        for i in range(data_length):
            label = datasets[i][-1]
            if label not in label_count:
                label_count[label] = 0
            label_count[label] += 1
        ent = -sum([(p / data_length) * log(p / data_length, 2)
                    for p in label_count.values()])
        return ent

    # 经验条件熵
    def condition_entropy(self,datasets,axis = 0):
        data_length = len(datasets)
        feature_sets = {}
        for i in range(data_length):
            feature = datasets[i][axis]
            if feature not in feature_sets:
                feature_sets[feature] = []
            feature_sets[feature].append(datasets[i])
        condi_ent = sum([ (len(p) / data_length)*self.entropy(p) for p in feature_sets.values()])
        return condi_ent

    # 信息增益
    @staticmethod
    def info_gain(ent,condi_entropy):
        return ent - condi_entropy


    def info_gain_train(self, datasets):
        count = len(datasets[0]) - 1
        ent = self.entropy(datasets)
        best_feature = []
        for c in range(count):
            c_info_gain = self.info_gain(ent,self.condition_entropy(datasets,axis=c))
            best_feature.append((c,c_info_gain))
            print("特征（{}）的信息增益为： {:.3f}".format(labels[c],c_info_gain))
        best = max(best_feature, key=lambda x:x[-1])
        return best

    def train(self,train_data):
        _,y_train,features = train_data.iloc[:,:-1],train_data.iloc[:,-1],train_data.columns[:-1]
        # 1,若D中实例属于同一类Ck，则T为单节点树，并将类Ck作为结点的类标记，返回T
        if  len(y_train.value_counts()) == 1:
            return Node(root=True, label = y_train.iloc[0])

        # 2, 若A为空，则T为单节点树，将D中实例树最大的类Ck作为该节点的类标记，返回T
        if len(features) == 0:
            return Node(root= True, label=y_train.value_counts().sort_values(ascending=False).index[0])

        # 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
        max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
        max_feature_name = labels[max_feature]

        # 4,Ag的信息增益小于阈值eta,则置T为单节点树，并将D中是实例数最大的类Ck作为该节点的类标记，返回T
        if max_info_gain < self.epsilon:
            return Node(root=True,label= y_train.value_counts().sort_values(ascending=False).index[0])

        # 5,构建Ag子集
        node_tree = Node(root = False,feature_name= max_feature_name, feature= max_feature)

        feature_list = train_data[max_feature_name].value_counts().index
        for f in feature_list:
            sub_train_df = train_data.loc[train_data[max_feature_name] == f].drop([max_feature_name],axis=1)
            # 6, 递归生成树
            sub_tree = self.train(sub_train_df)
            node_tree.add_node(f, sub_tree)
        return node_tree

    def fit(self,train_data):
        self._tree = self.train(train_data)
        return self._tree

    def predict(self,X_test):
        return self._tree.predict(X_test)

datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)
print(tree)

print(dt.predict(['老年', '否', '否', '一般']))

{'label:': None, 'feature': 2, 'tree': {'否': {'label:': None, 'feature': 1, 'tree': {'否': {'label:': '否', 'feature': None, 'tree': {}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}, '是': {'label:': '是', 'feature': None, 'tree': {}}}}
'否'

scikit-learn 实现

当然，我们也可以直接用sklearn来实现决策树

# scikit-learn 实现
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    # print(data)
    return data[:,:4], data[:,-1]

X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)


from sklearn.tree import DecisionTreeClassifier

clf = DecisionTreeClassifier()
clf.fit(X_train, y_train)
print(clf.fit(X_train, y_train))
print(clf.score(X_test, y_test))

第5章决策树-习题

习题5.1

根据表5.1所给的训练数据集，利用信息增益比（C4.5算法）生成决策树。

解答：

表5.1 贷款申请样本数据表

ID	年龄	有工作	有自己的房子	信贷情况	类别
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

from sklearn.tree import DecisionTreeClassifier
from sklearn import preprocessing
import numpy as np
import pandas as pd

from sklearn import tree
import graphviz

features = ["年龄", "有工作", "有自己的房子", "信贷情况"]
X_train = pd.DataFrame([
    ["青年", "否", "否", "一般"],
    ["青年", "否", "否", "好"],
    ["青年", "是", "否", "好"],
    ["青年", "是", "是", "一般"],
    ["青年", "否", "否", "一般"],
    ["中年", "否", "否", "一般"],
    ["中年", "否", "否", "好"],
    ["中年", "是", "是", "好"],
    ["中年", "否", "是", "非常好"],
    ["中年", "否", "是", "非常好"],
    ["老年", "否", "是", "非常好"],
    ["老年", "否", "是", "好"],
    ["老年", "是", "否", "好"],
    ["老年", "是", "否", "非常好"],
    ["老年", "否", "否", "一般"]
])
y_train = pd.DataFrame(["否", "否", "是", "是", "否", 
                        "否", "否", "是", "是", "是", 
                        "是", "是", "是", "是", "否"])
# 数据预处理
le_x = preprocessing.LabelEncoder()
le_x.fit(np.unique(X_train))
X_train = X_train.apply(le_x.transform)
le_y = preprocessing.LabelEncoder()
le_y.fit(np.unique(y_train))
y_train = y_train.apply(le_y.transform)
# 调用sklearn.DT建立训练模型
model_tree = DecisionTreeClassifier()
model_tree.fit(X_train, y_train)

# 可视化
dot_data = tree.export_graphviz(model_tree, out_file=None,
                                    feature_names=features,
                                    class_names=[str(k) for k in np.unique(y_train)],
                                    filled=True, rounded=True,
                                    special_characters=True)
graph = graphviz.Source(dot_data)
graph

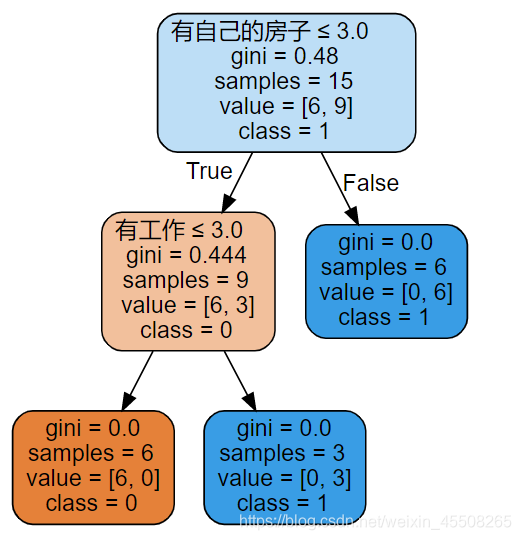
习题5.2

已知如表5.2所示的训练数据，试用平方误差损失准则生成一个二叉回归树。
表5.2 训练数据表

$xi$	1	2	3	4	5	6	7	8	9	10
$yi$	4.50	4.75	4.91	5.34	5.80	7.05	7.90	8.23	8.70	9.00

解答：
  决策树的生成就是递归地构建二叉决策树的过程，对回归树用平方误差最小化准则，对分类树用基尼指数（Gini index）最小化准则，进行特征选择，生成二叉树。

import numpy as np


class LeastSqRTree:
    def __init__(self, train_X, y, epsilon):
        # 训练集特征值
        self.x = train_X
        # 类别
        self.y = y
        # 特征总数
        self.feature_count = train_X.shape[1]
        # 损失阈值
        self.epsilon = epsilon
        # 回归树
        self.tree = None

    def _fit(self, x, y, feature_count, epsilon):
        # 选择最优切分点变量j与切分点s
        (j, s, minval, c1, c2) = self._divide(x, y, feature_count)
        # 初始化树
        tree = {"feature": j, "value": x[s, j], "left": None, "right": None}
        if minval < self.epsilon or len(y[np.where(x[:, j] <= x[s, j])]) <= 1:
            tree["left"] = c1
        else:
            tree["left"] = self._fit(x[np.where(x[:, j] <= x[s, j])],
                                     y[np.where(x[:, j] <= x[s, j])],
                                     self.feature_count, self.epsilon)
        if minval < self.epsilon or len(y[np.where(x[:, j] > s)]) <= 1:
            tree["right"] = c2
        else:
            tree["right"] = self._fit(x[np.where(x[:, j] > x[s, j])],
                                      y[np.where(x[:, j] > x[s, j])],
                                      self.feature_count, self.epsilon)
        return tree

    def fit(self):
        self.tree = self._fit(self.x, self.y, self.feature_count, self.epsilon)

    @staticmethod
    def _divide(x, y, feature_count):
        # 初始化损失误差
        cost = np.zeros((feature_count, len(x)))
        # 公式5.21
        for i in range(feature_count):
            for k in range(len(x)):
                # k行i列的特征值
                value = x[k, i]
                y1 = y[np.where(x[:, i] <= value)]
                c1 = np.mean(y1)
                y2 = y[np.where(x[:, i] > value)]
                c2 = np.mean(y2)
                y1[:] = y1[:] - c1
                y2[:] = y2[:] - c2
                cost[i, k] = np.sum(y1 * y1) + np.sum(y2 * y2)
        # 选取最优损失误差点
        cost_index = np.where(cost == np.min(cost))
        # 选取第几个特征值
        j = cost_index[0][0]
        # 选取特征值的切分点
        s = cost_index[1][0]
        # 求两个区域的均值c1,c2
        c1 = np.mean(y[np.where(x[:, j] <= x[s, j])])
        c2 = np.mean(y[np.where(x[:, j] > x[s, j])])
        return j, s, cost[cost_index], c1, c2

train_X = np.array([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]).T
y = np.array([4.50, 4.75, 4.91, 5.34, 5.80, 7.05, 7.90, 8.23, 8.70, 9.00])

model_tree = LeastSqRTree(train_X, y, .2)
model_tree.fit()
model_tree.tree

{'feature': 0,
 'value': 5,
 'left': {'feature': 0, 'value': 3, 'left': 4.72, 'right': 5.57},
 'right': {'feature': 0,
  'value': 7,
  'left': {'feature': 0, 'value': 6, 'left': 7.05, 'right': 7.9},
  'right': {'feature': 0, 'value': 8, 'left': 8.23, 'right': 8.85}}}

根据上面程序的输出，可得到用平方误差损失准则生成一个二叉回归树：
$$f(x)=\{\begin{array}{ll}4.72& x\le 3\\ 5.57& 3<x\le 5\\ 7.05& 5<x\le 6\\ 7.9& 6<x\le 7\\ 8.23& 7<x\le 8\\ 8.85& x>8\end{array}$$

习题5.3

  证明 CART 剪枝算法中，当$\alpha$确定时，存在唯一的最小子树$T_{\alpha }$使损失函数$C_{\alpha }(T)$最小。

解答：
**第1步：**内部节点是否剪枝只与以该节点为根节点的子树有关。
剪枝过程：
计算子树的损失函数：$$C_{\alpha }(T)=C(T)+\alpha$$其中，$C(T)=\sum _{t=1}^{|T|}{N}_t(1-\sum _{k=1}^K(\frac{N_{tk}}{N_t}{)}^2)$，$|T|$是叶结点个数，$K$是类别个数。
有剪枝前子树$T_0$，剪枝后子树$T_1$，满足$C_{\alpha }(T_1)⩽C_{\alpha }(T_0)$则进行剪枝。

---

**第2步（反证法）：**假设当$\alpha$确定时，存在两颗子树$T_1,T_2$都使得损失函数$C_{\alpha }$最小。
第1种情况：假设被剪枝的子树在同一边，易知其中一个子树会由另一个子树剪枝而得到，故不可能存在两个最优子树，原结论得证。
第2种情况：假设被剪枝的子树不在同一边，易知被剪枝掉的子树都可以使损失函数$C_{\alpha }$最小，故两颗子树都可以继续剪枝，故不可能存在两个最优子树，原结论得证。

习题5.4

  证明 CART 剪枝算法中求出的子树序列 { T 0 , T 1 , ⋯   , T n } \{T_0,T_1,\cdots,T_n\} {T0​,T1​,⋯,Tn​}分别是区间$\alpha \in [{\alpha }_i,{\alpha }_{i+1})$的最优子树$T_{\alpha }$，这里$i=0,1,\cdots ,n,0={\alpha }_0<{\alpha }_1<\cdots ,{\alpha }_n<+\infty$。

解答：
原结论可以表述为：将$\alpha$从小增大，$0={\alpha }_0<{\alpha }_1<\cdots <{\alpha }_n<+\infty$，在每个区间$[{\alpha }_i,{\alpha }_{i+1})$中，子树$T_i$是这个区间里最优的。
**第1步：**易证，当$\alpha =0$时，整棵树$T_0$是最优的，当$\alpha \to +\infty$时，根结点组成的单结点树（即$T_n$）是最优的。

---

第2步：
  由于每次剪枝剪的都是某个内部结点的子结点，也就是将某个内部结点的所有子结点回退到这个内部结点里，并将这个内部结点作为叶子结点。因此在计算整体的损失函数时，这个内部结点以外的值都没变，只有这个内部结点的局部损失函数改变了，因此本来需要计算全局的损失函数，但现在只需要计算内部结点剪枝前和剪枝后的损失函数。
从整体树$T_0$开始剪枝，对$T_0$的任意内部结点$t$
剪枝前的状态：有$|T_t|$个叶子结点，预测误差是$C(T_t)$
剪枝后的状态：只有本身一个叶子结点，预测误差是$C(t)$
因此剪枝前的以$t$结点为根结点的子树的损失函数是$$C_{\alpha }(T_t)=C(T_t)+\alpha |T_t|$$剪枝后的损失函数是$$C_{\alpha }(t)=C(t)+\alpha$$易得，一定存在一个$\alpha$使得$C_{\alpha }(T_t)=C_{\alpha }(t)$，这个值为$$\alpha =\frac{C(t)-C(T_t)}{|T_t|-1}$$可知，找到$\alpha$即找到了子结点$t$，即完成了剪枝，得到最优子树$T_1$
根据书中第73页，采用以下公式计算剪枝后整体损失函数减少的程度：$$g(t)=\frac{C(t)-C(T_t)}{|T_t|-1}$$在$T_0$中剪去$g(t)$最小的$T_t$，将得到的子树作为$T_1$，同时将最小的$g(t)$设为${\alpha }_1$，$T_1$为区间$[{\alpha }_1,{\alpha }_2)$的最优子树。
依次类推，子树$T_i$是区间$[{\alpha }_i,{\alpha }_{i+1})$里最优的，原结论得证。