1、RNN为什么容易梯度消失和梯度爆炸？

每次提到RNN最先遇到的问题肯定是梯度消失和梯度爆炸，那么什么是梯度消失和梯度爆炸？RNN中为什么会出现这个问题呢？

梯度消失和梯度爆炸是深度学习模型，特别是在训练递归神经网络（RNN）和深度前馈神经网络时可能遇到的两个主要问题。这两个问题都源于神经网络中梯度的连乘效应。

• 梯度消失（Vanishing Gradients）
  在反向传播过程中，每个层的梯度是前一层梯度和当前层激活函数梯度的乘积。如果激活函数的导数小于1（如Sigmoid或Tanh函数），在多层网络中连乘后，梯度值可能会指数级下降，导致深层网络的权重更新非常缓慢，几乎停止学习。这种现象称为梯度消失。
• 梯度爆炸（Exploding Gradients）
  与梯度消失相反，如果网络中的梯度值在反向传播过程中指数级增长，那么就会发生梯度爆炸。这通常是由于权重的初始化过大或者网络架构设计不当导致的。梯度爆炸会导致网络权重的大幅更新，从而使得学习过程变得不稳定，网络无法收敛。

梯度消失和梯度爆炸是RNN在反向传播过程中常见的问题，RNN的反向传播是通过时间的反向传播”（Backpropagation Through Time，BPTT），其运行流程与一般的反向传播大有不同。在不同类型NLP任务会有不同的输出层结构、会有不同的标签输出方式。例如，在对词语/样本进行预测的任务中（情感分类、词性标注、时间序列等任务），RNN会在每个时间步都输出词语对应的相应预测标签；但是，在对句子进行预测的任务中（例如，生成式任务、seq2seq的任务、或以句子为单位进行标注、分类的任务），RNN很可能只会在最后一个时间步输出句子相对应的预测标签。输出标签的方式不同，反向传播的流程自然会有所区别。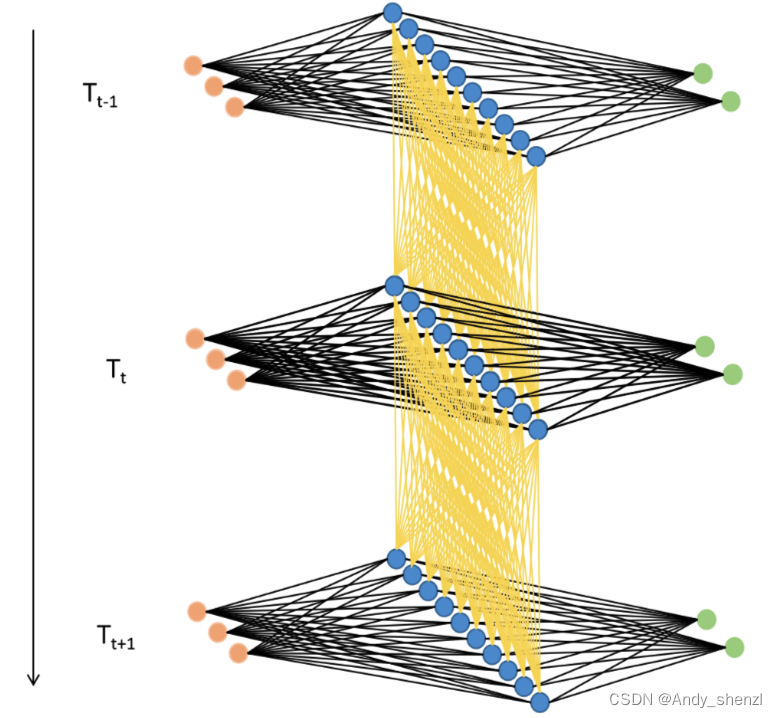

假设现在我们有一个最为简单的RNN，需要完成针对每个词语的情感分类任务。该RNN由输入层、一个隐藏层和一个输出层构成，全部层都没有截距项，总共循环$t$个时间步。该网络的输入数据为$X$，输出的预测标签为$\hat{y}$，真实标签为$y$，激活函数为$\sigma$，输入层与隐藏层之间的权重矩阵为$W_{xh}$，隐藏层与输出层之间的权重矩阵为$W_{hy}$，隐藏层与隐藏层之间的权重为$W_{hh}$，损失函数为$L(\hat{y},y)$，t时刻的损失函数我们简写为$L_t$。此时，在时间步t上，这个RNN的正向传播过程可以展示如下：

$$\begin{array}{rl}{\mathbf{h}}_t& =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1})\\ & =\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_{t-1}+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-2}))\\ & \\ {\hat{\mathbf{y}}}_t& ={\mathbf{W}}_{hy}{\mathbf{h}}_t\\ & \\ L_t& =L({\hat{\mathbf{y}}}_t，{\mathbf{y}}_t)\end{array}$$

不难发现，RNN中存在至少三个权重矩阵需要迭代：输入层与隐藏层之间的权重矩阵$W_{xh}$，隐藏层与输出层之间的权重矩阵$W_{hy}$，隐藏层与隐藏层之间的权重$W_{hh}$。当完成正向传播后，我们需要在反向传播过程中对以上三个权重求解梯度、并迭代权重，以$W_{hh}$为例——

时间步t，我们需要求解的其中一个梯度为：

$$\begin{array}{r}3.1）\frac{\partial L_t}{\partial W_{hh}}\\ \end{array}$$

根据之前的数学流程，$L_t$可以展开展示为：

$$\begin{array}{rl}{L}_t& =L({\hat{\mathbf{y}}}_t,{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}{\mathbf{h}}_t,{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}),{\mathbf{y}}_t)\end{array}$$

可见，$L_t$是以${\hat{y}}_t$为自变量的函数，${\hat{y}}_t$是以$W_{hy}$和$h_t$为自变量的函数，$h_t$又是以$W_{xh}$和$W_{hh}$为自变量的函数，因此要求解上面三个梯度，其实是需要对复合函数进行求导。根据链式法则规则，如果y = f(u)并且u = g(x)，那y直接对x求导的公式则可写成：

$$\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}$$

因此根据链式法则，我们有：

$$1)\frac{\partial L_t}{\partial W_{hy}}=\frac{\partial L_t}{\partial {\hat{y}}_t}\ast \frac{\partial {\hat{y}}_t}{\partial W_{hy}}$$

$$2)\frac{\partial L_t}{\partial W_{xh}}=\frac{\partial L_t}{\partial {\hat{y}}_t}\ast \frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial W_{xh}}$$

$$3)\frac{\partial L_t}{\partial W_{hh}}=\frac{\partial L_t}{\partial {\hat{y}}_t}\ast \frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial W_{hh}}$$

好了，到这里为止循环神经网络的反向传播过程都与普通深度神经网络类似，但有的小伙伴可能已经注意到了，上面的公式2和3中存在一个关键问题，那就是$h_t$作为一个复合函数，不止能以$W_{xh}$和$W_{hh}$为自变量，还能以上层的隐藏状态$h_{t-1}$作为自变量，而$h_{t-1}$本身又是以$W_{xh}$和$W_{hh}$为自变量的函数：

$$\begin{array}{rl}{L}_t& =L({\hat{\mathbf{y}}}_t,{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}{\mathbf{h}}_t,{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}),{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-2}),{\mathbf{y}}_t)\end{array}$$

此时你发现了吗？在求解$L_t$对$W_{hh}$的导数时，不止可以求解上面所写的式子3，还可以继续对嵌套函数求解得到下面的梯度3——

$$\begin{array}{rl}3.2)\frac{\partial L_t}{\partial W_{hh}}& =\frac{\partial L_t}{\partial {\hat{y}}_t}\ast \frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial h_{t-1}}\ast \frac{\partial h_{t-1}}{\partial W_{hh}}\\ & \end{array}$$

甚至，我们还可以将$h_{t-1}$继续拆解为$\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_{t-1}+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-2})$，还可以将$h_{t-2}$继续拆解为$\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_{t-2}+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-3})$，我们可以将嵌套函数无止尽地拆解下去，直到拆到${\mathbf{h}}_1=\sigma ({\mathbf{W}}_{xh}{\mathbf{X}}_1+{\mathbf{W}}_{hh}{\mathbf{h}}_0)$为止。在这个过程中，只要拆解足够多，我们可以从$L_t$求解出t个针对和$W_{hh}$的导数。因此惊人的事实是，在时间步t上，我们可以计算t个用于迭代$W_{xh}$和$W_{hh}$的梯度！

当我们将损失函数一直拆解到最后一层，且假设激活函数为恒等函数（为了简化数学流程）——

$$\begin{array}{rl}{L}_t& =L({\hat{\mathbf{y}}}_t,{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}{\mathbf{h}}_t,{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}),{\mathbf{y}}_t)\\ & \\ & =L({\mathbf{W}}_{hy}({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}({\mathbf{W}}_{xh}{\mathbf{X}}_{t-1}+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-2})),{\mathbf{y}}_t)\\ & \\ & ⋮\\ & \\ & =L({\mathbf{W}}_{hy}({\mathbf{W}}_{xh}{\mathbf{X}}_t+{\mathbf{W}}_{hh}({\mathbf{W}}_{xh}{\mathbf{X}}_{t-1}+\cdots +{\mathbf{W}}_{hh}({\mathbf{W}}_{xh}{\mathbf{X}}_1+{\mathbf{W}}_{hh}{\mathbf{h}}_0))...),{\mathbf{y}}_t)\end{array}$$

在这个彻底拆解后的公式上，我们可以求解出嵌套了t层的$W_{hh}$的梯度（如公式3.t）：

$$\begin{array}{rl}3.t)\frac{\partial L_t}{\partial W_{hh}}& =\frac{\partial L_t}{\partial {\hat{y}}_t}\ast \frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial h_{t-1}}\ast \frac{\partial h_{t-1}}{\partial h_{t-2}}\ast ...\ast \frac{\partial h_2}{\partial h_1}\ast \frac{\partial h_1}{\partial W_{hh}}\\ & \end{array}$$

此时在这个公式中，许多偏导数的求解就变得非常简单，例如：

$$\begin{array}{rl}& \because {\hat{y}}_t=W_{hy}{h}_t,\therefore \frac{\partial {\hat{y}}_t}{\partial h_t}=W_{hy}\\ & \\ & \because h_t=W_{xh}{X}_t+W_{hh}{h}_{t-1},\therefore \frac{\partial h_t}{\partial h_{t-1}}=W_{hh}\\ & \\ & \because h_{t-1}=W_{xh}{X}_{t-1}+W_{hh}{h}_{t-2},\therefore \frac{\partial h_{t-1}}{\partial h_{t-2}}=W_{hh}\\ & \\ & ⋮\\ & \\ & \because h_2=W_{xh}{X}_2+W_{hh}{h}_1,\therefore \frac{\partial h_2}{\partial h_1}=W_{hh}\\ & \\ & \because h_1=W_{xh}{X}_1+W_{hh}{h}_0,\therefore \frac{\partial h_1}{\partial W_{hh}}=h_0\end{array}$$

所以最终的梯度表达式为：

$$\begin{array}{rl}3.t)\frac{\partial L_t}{\partial W_{hh}}& =\frac{\partial L_t}{\partial {\hat{y}}_t}\ast \frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial h_{t-1}}\ast \frac{\partial h_{t-1}}{\partial h_{t-2}}\ast ...\ast \frac{\partial h_2}{\partial h_1}\ast \frac{\partial h_1}{\partial W_{hh}}\\ & \\ & =\frac{\partial L_t}{\partial {\hat{y}}_t}\ast W_{hy}\ast W_{hh}\ast W_{hh}\ast ...\ast W_{hh}\ast h_0\\ & \\ & =\frac{\partial L_t}{\partial {\hat{y}}_t}\ast W_{hy}\ast (W_{hh}{)}^{t-1}\ast h_0\\ & \end{array}$$

不难发现，在这个梯度表达式中出现了$(W_{hh}{)}^{t-1}$这样的高次项，这就是循环神经网络非常容易梯度爆炸和梯度消失的根源所在——假设$W_{hh}$是一个小于1的值，那$(W_{hh}{)}^{t-1}$将会非常接近于0，从而导致梯度消失；假设$W_{hh}$大于1，那$(W_{hh}{)}^{t-1}$将会接近无穷大，从而引发梯度爆炸，其中梯度消失发生的可能性又远远高于梯度爆炸。

在深度神经网络中，在应用链式法则后，我们也会面临复合函数梯度连乘的问题，但由于普通神经网络中并不存在“权值共享”的现象，因此每个偏导数的表达式求解出的值大多是不一致的，在连乘的时候有的偏导数值较大、有的偏导数值较小，相比之下就不那么容易发生梯度爆炸或梯度消失问题的问题。

2、LSTM能够解决梯度消失和梯度爆炸问题吗？

来简单梳理一下LSTM的数学流程——

遗忘门：$$f_t=\sigma (W_{xf}\cdot x_t+W_{hf}\cdot h_{t-1})$$

输入门：$$i_t=\sigma (W_{xi}\cdot x_t+W_{hi}\cdot h_{t-1})$$

潜在细胞状态：$${\tilde{C}}_t=\tanh (W_{xc}\cdot x_t+W_{hc}\cdot h_{t-1})$$

细胞状态更新：$$C_t=f_t\cdot C_{t-1}+i_t\cdot {\tilde{C}}_t$$

输出门：$$o_t=\sigma (W_{xo}\cdot x_t+W_{ho}\cdot h_{t-1})$$

当下时刻输出：$$h_t=o_t\cdot \tanh (C_t)$$

LSTM在反向传播中的梯度求解链路可以被可视化为：

假设我们现在计算$\frac{\partial L_t}{\partial W_{hf}}$，则有——

$$\begin{array}{rl}3.t)\frac{\partial L_t}{\partial W_{hf}}& =\frac{\partial L_t}{\partial {\hat{y}}_t}\ast \frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial C_t}\ast \frac{\partial C_t}{\partial f_t}\ast \frac{\partial f_t}{\partial h_{t-1}}\ast \frac{\partial h_{t-1}}{\partial C_{t-1}}...\ast \frac{\partial f_1}{\partial W_{hf}}\\ & \\ & =\frac{\partial L_t}{\partial {\hat{y}}_t}\frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial C_t}\ast [\frac{\partial C_t}{\partial C_{t-1}}\ast \frac{\partial C_{t-1}}{\partial C_{t-2}}...\ast \frac{\partial C_2}{\partial C_1}]\ast \frac{\partial C_1}{\partial f_1}\ast \frac{\partial f_1}{\partial w_{hf}}\\ & \\ & =\frac{\partial L_t}{\partial {\hat{y}}_t}\frac{\partial {\hat{y}}_t}{\partial h_t}\ast \frac{\partial h_t}{\partial C_t}\ast [f_t\ast f_{t-1}\ast f_{t-2}...\ast f_1]\ast \frac{\partial C_1}{\partial f_1}\ast \frac{\partial f_1}{\partial w_{hf}}\\ & \end{array}$$

通过避开共享权重的相乘，LSTM将循环网络梯度爆炸和梯度消失的危险性降低到了一般神经网络的水平。由于$f_t$在0～1之间，因此就意味着梯度爆炸的风险将会很小，至于会不会梯度消失，取决于$f_t$是否接近于1。如果当下时刻的长期记忆比较依赖于历史信息，那么$f_t$就会接近于1，这时候历史的梯度信息也正好不容易消失；如果$f_t$很接近于0，那么就说明当下的长期记忆不依赖于历史信息，这时候就算梯度消失也无妨了。

$f_t$在0～1之间这个特性决定了它梯度爆炸的风险很小，同时$f_t$表明了模型对历史信息的依赖性，也正好是历史梯度的保留程度，两者相互自洽，所以LSTM也能较好地缓解梯度消失问题。因此，LSTM同时较好地缓解了梯度消失/爆炸问题。

【有趣的小事实】
在今天看来，梯度消失和梯度爆炸是阻碍RNN能够被正常训练的关键问题，但在1990年代，算力和数据都十分缺乏、神经网络层数往往较浅、在研究中所需的迭代次数很少，序列长度也较短，因此RNN的梯度消失和梯度爆炸问题并没有这么显著。相对的，当时大量的研究（包括LSTM）都围绕着两个更加显著、更加直观的问题展开，其中一个问题是权重冲突（Weight Conflict），另一个问题是长短期信息冲突（Long-Short Term Information Conflict）。所以当我们追溯LSTM的结构与解决梯度消失、梯度爆炸问题有任何关联的时候，其实是无法找到其中的关联的。

3、LSTM中为什么$C_t$可以获得长期记忆

我们来看下公式
遗忘门：$$f_t=\sigma (W_{xf}\cdot x_t+W_{hf}\cdot h_{t-1})$$

输入门：$$i_t=\sigma (W_{xi}\cdot x_t+W_{hi}\cdot h_{t-1})$$

潜在细胞状态：$${\tilde{C}}_t=\tanh (W_{xc}\cdot x_t+W_{hc}\cdot h_{t-1})$$

细胞状态更新：$$C_t=f_t\cdot C_{t-1}+i_t\cdot {\tilde{C}}_t$$

输出门：$$o_t=\sigma (W_{xo}\cdot x_t+W_{ho}\cdot h_{t-1})$$

当下时刻输出：$$h_t=o_t\cdot \tanh (C_t)$$

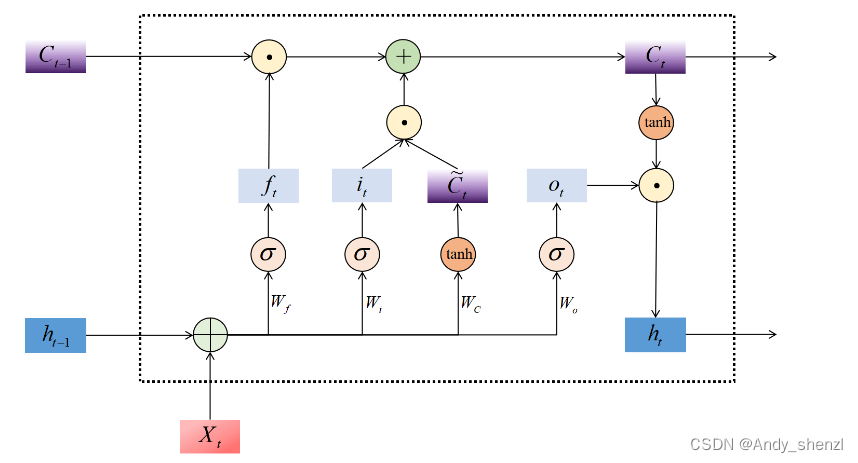
对于负责长期记忆的$C_t$，

$$C_t=f_t\cdot C_{t-1}+i_t\cdot {\tilde{C}}_t$$
我们可以发现$C_t$是根据$C_{t-1}$计算而来，$C_{t-1}$同样也是来自于上一个记忆细胞$C_{t-2}$，也就是这个细胞时在整个时间步上持续迭代的所以会记住长期的信息

而对于负责短期记忆的$$h_t=o_t\cdot \tanh (C_t)$$
在$h_t$的计算中并没有来自于$h_{t-1}$的信息，所以是无法记住长期信息的