武汉大学信管专业期末复习系列——《数据结构》(python实现) 树与二叉树
武汉大学信管专业期末复习系列——《数据结构》(python实现) 树与二叉树
*************************************************************************
免费订阅我的“信息管理与信息系统专业课期末复习”专栏,后续会相继推出其他专业课和平台课的期末复习资料哦
*************************************************************************
目录
(一)树
1. 树的定义
个数为0,则我们称该树为空树;否则称为非空树。
一棵树是 n (n≥0) 个结点的有限集 T(可为空),T 非空时满足:
2. 树的相关概念
- 1. 结点的度:每个结点拥有子树的数目被称为结点的度
- 2. 树的度:树内所有结点度的最大值被称为该树的度。
-
3. 树的深度:树中所有结点的层次的最大值被称为该树的深度(也称为“高度”)。通常将空树的深度定义为0
-
4. 叶子结点:度为0的结点被称为叶子结点(也 被称为“终端结点”)
-
5. 分支结点:度不为0的结点被称为分支结点 (也被称为“非终端结点”)
- 6. 孩子结点:树中任何一个结点的子树的根结点被称为这一结点的孩子结点(也被称为“后继结点”)。
- 7. 双亲结点:对于树中任何一个结点而言,若其具有孩子结点,那么我们把这个结点就称为其孩子结点的双亲结点。
-
8.兄弟结点:同一双亲的孩子结点互相称为兄弟结点。
-
9.祖先结点:从根结点到树中任一结点所经过的所有结点被称为该结点的祖先结点。
- 10.子孙结点:树中以某一结点为根的子树中任一结点均被称为该根结点的子孙结点
-
11. 结点的层次:从根结点开始定义,通常将根结点设定为第一层,根的孩子结点为第二层依次类推,若某一结点在第i层,则其子树的根在第i+1层。
-
12. 有序树:如果将树中结点的各子树看成从左至右是有次序的,这些子树的位置是不能被改变的,则称该树为有序树。
-
13. 无序树:如果将树中结点的各子树看成是无次序的,这些子树的位置是能够被改变的,则称该树为无序树。
3. 树的存储
树的存储方式一共有3种,分别是双亲表示法、孩子表示法和孩子兄弟表示法,下面一一介绍。
3.1 双亲表示法:
即每个树的节点存储数据域和指向双亲节点的指针域。这种表示方法可以方便的找到每个节点的双亲,如下图所示:
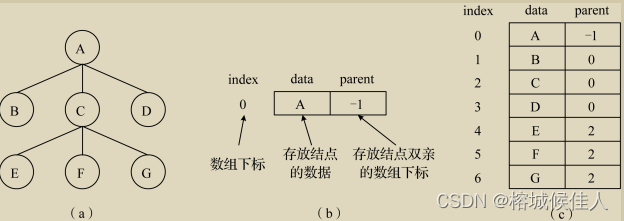
双亲表示法采用一个顺序数组按照层次遍历的顺序将所有节点存入,而每个节点就是包括节点的数据和该节点双亲的位置(在数组中的下标)
3.2 孩子表示法:
这里和双亲表示法不同(只涉及一个节点类和一个数组),孩子表示法需要两个节点类(一个是树中的所有节点,存储节点数据和指向它的第一个孩子节点的指针域;另一个是孩子节点,存储它在顺序数组中的位置和指向它下一个兄弟节点的指针域)和两个数据结构(一个数组,一个单链表)
首先用一个顺序数组按照层次遍历的顺序将所有的节点存入,然后将每个节点的所有孩子节点采用单链表的形式存储,并将其指针指向下一个兄弟节点。如下图所示:
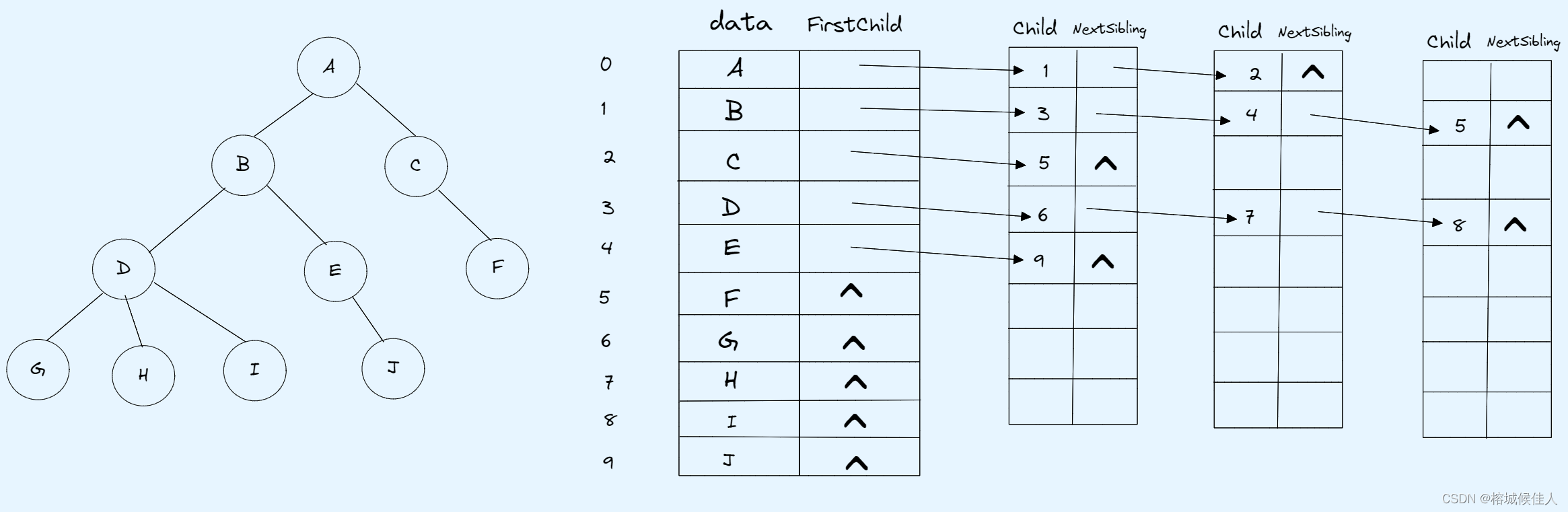
3.3 孩子兄弟表示法:
就是节点分别存放指向第一个孩子节点的指针、数据域、指向下一个兄弟节点的指针,然后也用顺序数组存储这些节点。如下图所示:
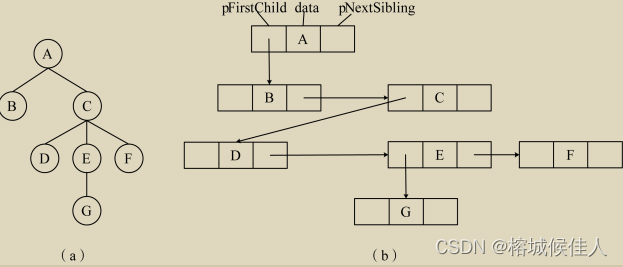
4. 树的遍历
4.1 先序遍历:
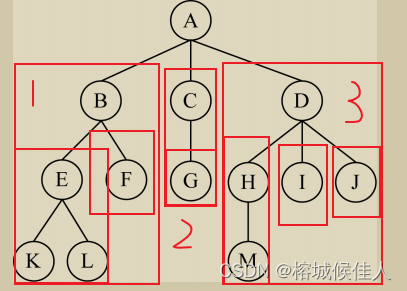
4.2 后序遍历:
后序遍历的过程如下:
(1)按照从左到右的顺序后序遍历根结点的每一棵子树。
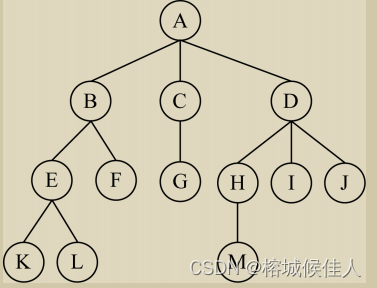
如下图所示:是先从左到右访问子树,最后再访问根节点。
这棵树的后序遍历结果为:KLEFBGCMHIJDA
4.3 层次遍历:
这个很简单了,就是从上到下,从左到右
所以这棵树层次遍历的结果是:ABCDEFGHIJKLM

(二)二叉树
1. 二叉树的定义:
2. 满二叉树与完全二叉树:
2.1 完全二叉树:
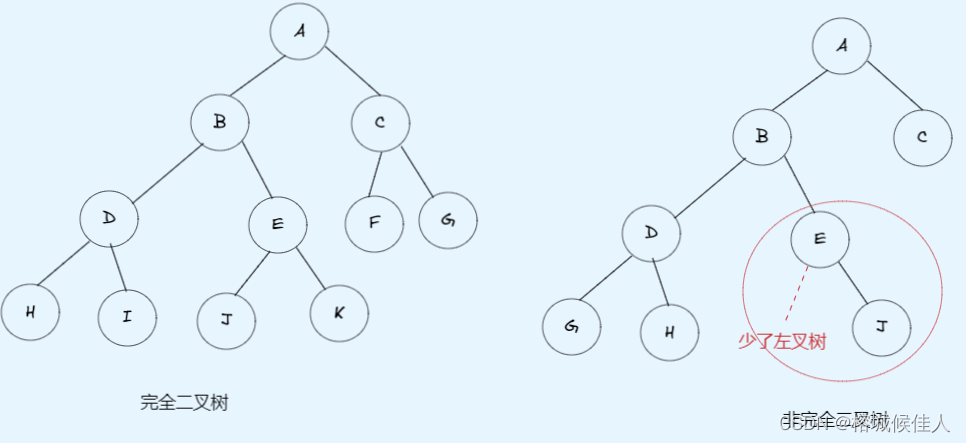
对一棵具有n个结点且深度为k的二叉树,从其根结点开始,按照结点所在的层次从小到大、同一层从左子树到右子树依次进行编号,则称其为完全二叉树。简单理解就是完全按照层次遍历的顺序展开,如果有右叉树则一定有左叉树,可以有左叉树而没有右叉树。如下图所示:
2.2 满二叉树:
是完全二叉树的特例,即除了最后一层的节点全是叶子结点以外,其他所有节点都有左右子树。如下图:
3. 二叉树的存储
3.1 顺序存储:
顺序存储即按照层次遍历的顺序存储,但会造成空间的浪费,因此只适用于完全二叉树或者满二叉树的存储。
具体步骤如下:
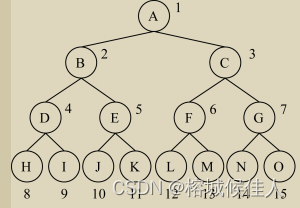
- 针对完全二叉树(包括了满二叉树):用一组地址连续的存储单元从根结点开始依次自上而下,并按层次从左到右存储完全二叉树上的各结点元素,即将完全二叉树编号为i的结点元素存储在下标为i数组元素中。
-
针对非完全二叉树: 先在树中增加一些并不存在的虚结点并使其成为一 棵完全二叉树,然后用与完全二叉树相同的方法对结 进行编号,再将编号为i的结点的值存放到数组下 标为i的数组单元中,虚结点不存放任何值。
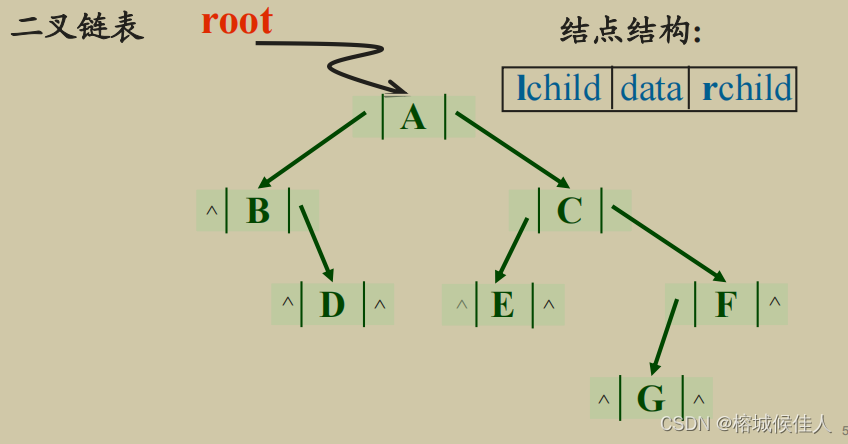
3.2 链式存储:
4. 二叉树的遍历
4.1 递归版本
4.1.1 先序遍历:
概念和树的线序遍历时一致的,也是先根节点,然后左子树,最后右子树。如下图所示:该树的先序遍历为:ABCDEFGHK
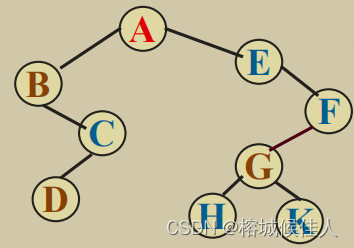
4.1.2 中序遍历:
这是树的遍历所没有的,具体来说就是先遍历左子树,再访问根节点,最后访问右子树(普通的数不一样有这种对称结构,也就没有中序遍历)。如下图所示:该树中序遍历的结果是:BDCAEHGKF
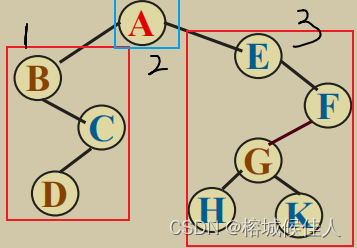
4.1.3 后序遍历:
和树的后序遍历一样,先左子树,再右子树,最后再访问根节点。如下图所示:该树后序遍历的结果是:DCBHKGFEA

4.1.4 层次遍历:
这个就很简单了,如下图所示:该树层次遍历的结果是:ABECFDGHK

4.2 非递归版本(侧重python代码逻辑的讲解)
4.2.1 先序遍历:
算法思想:从根节点开始从左子树访问,然后利用一个栈保存被访问的节点的右孩子节点。当一路沿着左子树访问到最后一个叶子结点的时候,再从栈里取出右孩子节点访问。
def PreOrderNonRecursive(self,Root):
StackTreeNode=[] # 用来存放当前被访问节点的右孩子节点的栈
tTreeNode=Root # 给定一棵二叉树的根节点
# ===========================================================================
while len(StackTreeNode) > 0 or tTreeNode is not None:
# 这个循环用来访问节点的值,根节点的访问完了以后默认是从左孩子节点开始的
while tTreeNode is not None:
self.VisitBinaryTreeNode(tTreeNode)
StackTreeNode.append(tTreeNode)
tTreeNode=tTreeNode.LeftChild # 可以看到访问的都是左孩子节点
# 在上面的循环结束以后,栈里已经存了很多右孩子节点,下面的判断语句就是把根节点换成
# 后孩子节点,然后再回到上面的循环去打印右孩子节点的信息
# ============================================================================
# ============================================================================
# 一旦左孩子节点是叶子结点,就来到下面这个判断语句,把根节点换成栈里的后孩子节点
if len(StackTreeNode)>0:
tTreeNode=StackTreeNode.pop()
tTreeNode=tTreeNode.RightChild
def VisitBinaryTreeNode(self,BinaryTreeNode):
"""用于打印节点信息"""
if BinaryTreeNode.data is not '#':
print(BinaryTreeNode.data)4.2.2 中序遍历:
算法思想:从根节点开始,沿着左子树方向一路访问,并把没有访问的节点(根节点)依次压入栈中,待访问到最后一个叶子结点时,再取出栈里的根节点访问,最后再对右子树进行同样的操作。
def InOrderNonRecursive(self,Root):
StackTreeNode=[] # 存放根节点的栈
tTreeNode=Root # 任意一棵二叉树的根节点
# ========================================================================
while len(StackTreeNode)>0 or tTreeNode is not None:
while tTreeNode is not None:
StackTreeNode.append(tTreeNode) # 把根节点压入栈里面
tTreeNode=tTreeNode.LeftChild # 左孩子节点成为新的根节点
# 上面的循环只有当遇到叶子结点并把它压入栈中才会停止,所以下面就是针对遇见叶子结
# 点也被压入栈中情况的判断语句
# =========================================================================
if len(StackTreeNode)>0:
# 第一次是取出叶子结点,然后就是路径上的所有根节点
tTreeNode=StackTreeNode.pop()
self.VisitBinaryTreeNode(tTreeNode)
tTreeNode=tTreeNode.RightChild
def VisitBinaryTreeNode(self,BinaryTreeNode):
"""访问节点信息的函数"""
if BinaryTreeNode.data is not '#':
print (BinaryTreeNode.data)4.2.3 后序遍历:
这个老师没讲,感兴趣的同学自行查询哈~
4.2.4 层次遍历:
算法思想:借助一个队列。在遍历开始时,首先将根结点入队, 然后每次从队列中取出队首元素进行处理,每处理一个结点,都是先访问该结点,再按从左到右的顺序把它的孩子结点依次入队。
def LevelOrder(self,Root):
tSequenceQueue=CircularSequenceQueue() # 创建队列
tSequenceQueue.InitQueue(100)
tSequenceQueue.EnQueue(Root) # 将根节点入队
tTreeNode=None # 指向每个被操作的节点的指针
# 将在这个循环完成层次遍历,条件就是队列不为空,为空的话说明遍历完了
while tSequenceQueue.IsEmptyQueue()==False:
tTreeNode=tSequenceQueue.DeQueue() # 节点出队
self.VisitBinaryTreeNode(tTreeNode) # 打印出队节点信息
# 两个判断语句分被将出队节点的左右孩子节点按从左到右的顺序放入栈中
if tTreeNode.LeftChild is not None:
tSequenceQueue.EnQueue(tTreeNode.LeftChild)
if tTreeNode.RightChild is not None:
tSequenceQueue.EnQueue(tTreeNode.RightChild)
def VisitBinaryTreeNode(self,BinaryTreeNode):
"""访问节点信息"""
if BinaryTreeNode.data is not '#':
print (BinaryTreeNode.data)5. 二叉树的构建
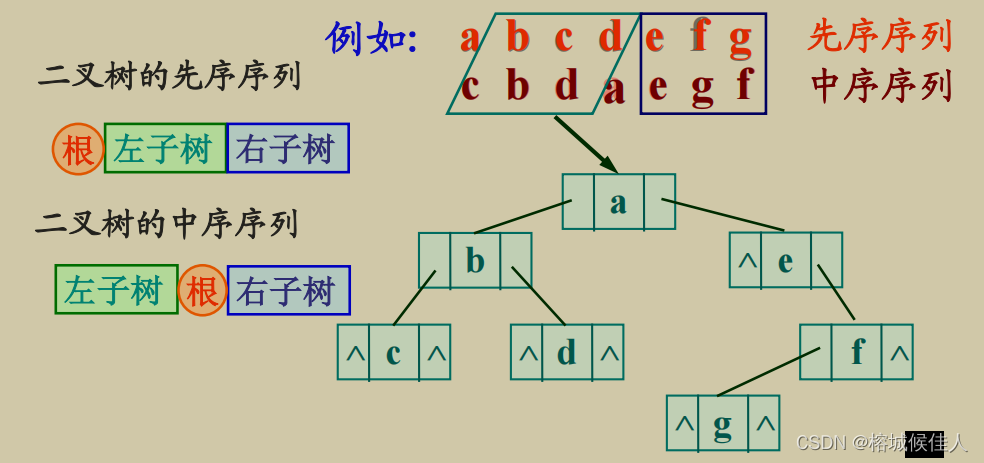
构建二叉树的四种方式:注意先根+后根遍历是无法确定唯一的二叉树的,因为两个方法都只能确定根节点,无法区分左右子树。

6. 二叉树的应用:
6.1 表达式树:
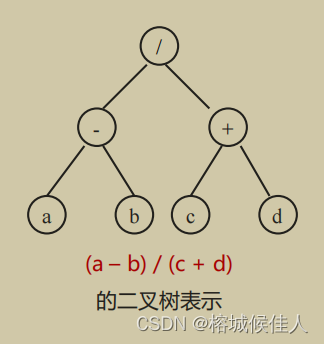
6.2 前缀、中缀、后缀表达式:

先序遍历二叉树可以获得前缀表达式,后序遍历二叉树可以获得后缀表达式。
表达式树法:
中缀转换成前后缀:表达式树的树叶是操作数,而其他的节点为操作符,根节点为优先级最低且靠右的操作符。举个栗子(中缀转成前缀):
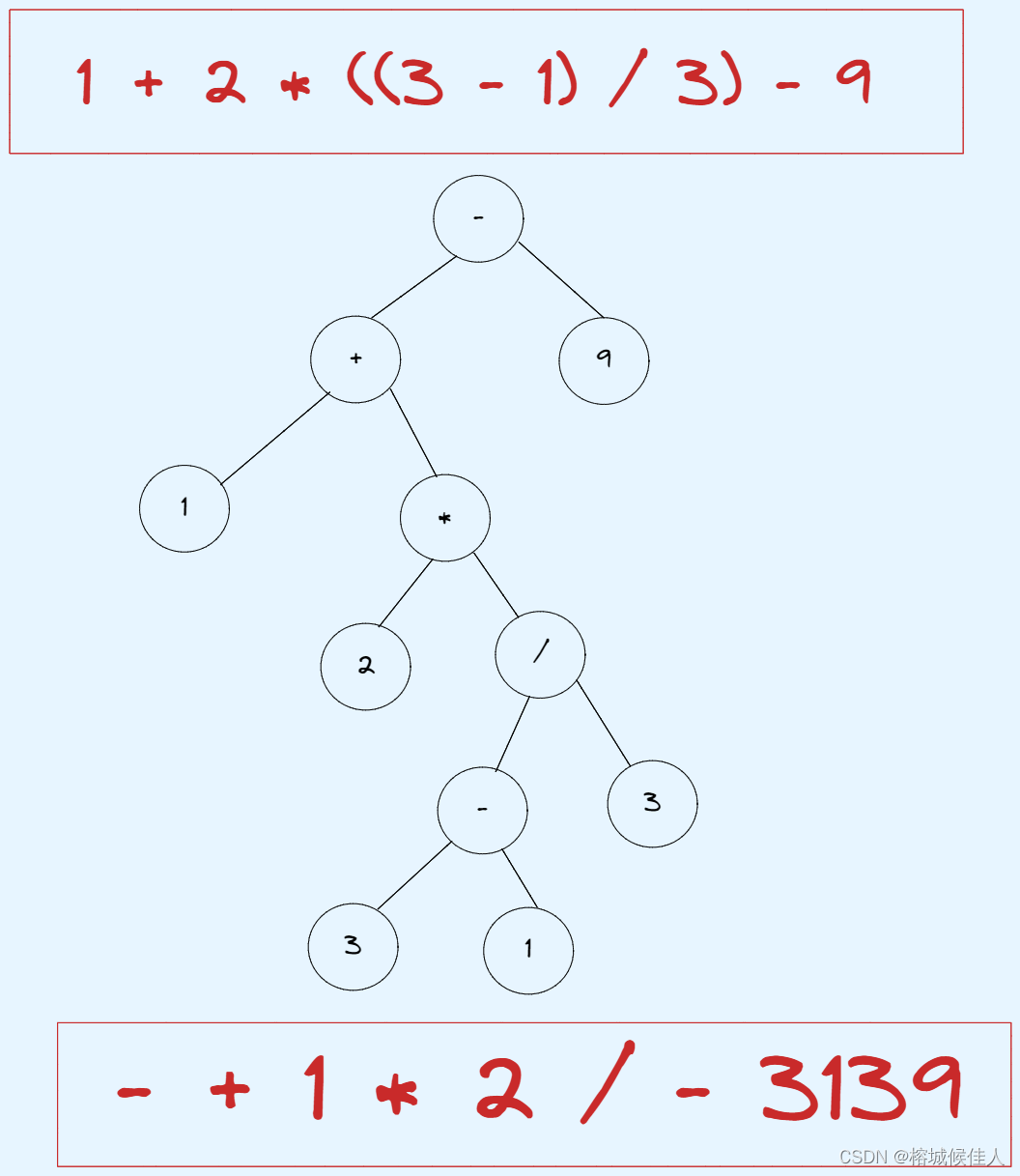
OK,树与二叉树暂时就复习到这里啦~下一篇将推出哈夫曼树的相关复习资料
如果你对这类复习文章感兴趣的话,可以免费订阅我的“信息管理与信息系统专业课期末复习”专栏,里面后续会推出信管专业其他专业课的期末复习资料。


GitCode 天启AI是一款由 GitCode 团队打造的智能助手,基于先进的LLM(大语言模型)与多智能体 Agent 技术构建,致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话,还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力,真正做到“一句话,让 Al帮你完成复杂任务”。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容









所有评论(0)