Coursera self-driving car Part1 Final Project——自动驾驶轨迹跟踪之Pure Pursuit纯跟踪算法推导及Python实现

1.Pure Pursuit原理

参考https://blog.csdn.net/weixin_39549161/article/details/88712443?spm=1001.2014.3001.5506

将小车简化为两轮自行车模型

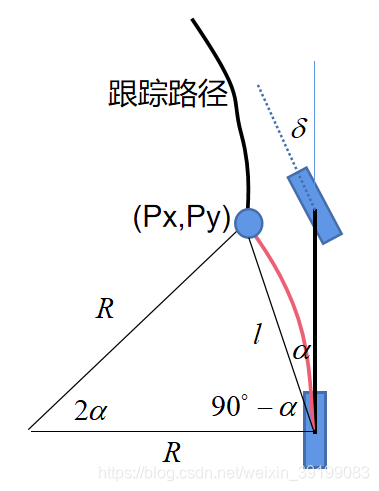
个人理解纯跟踪算法就是让无人驾驶车后轴中心，绕着转弯中心，按转弯半径的圆弧走到待跟踪路径的预瞄点上，预瞄距离l越小，越快收敛到参考轨迹，车辆就越激进。

根据正弦定理

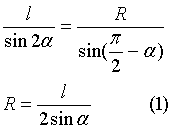
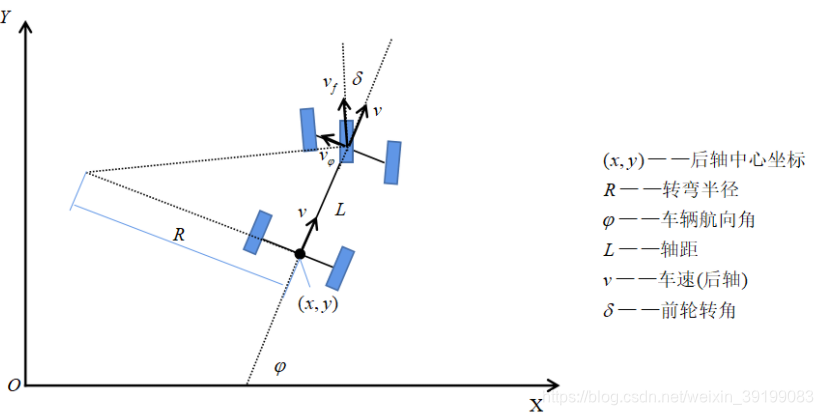
根据上图的几何关系，

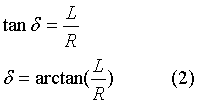
联立式(1),(2)

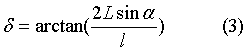
预瞄距离，如果为常数，在低速时效果可能很好，但在高速时太小的预瞄距离导致车辆过于激进出现振荡，所以通常让预瞄距离正比于车速v.       防止车速很小时,l过小加上一个常数偏置。参数k，l0由自己设置，k越小越激进。

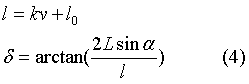
则(4)为最终的pure pursuit控制公式

2.python实现

算法原理非常简单，由式4可以看出，关键只要计算出预瞄距离，以及α即可求解当前时刻所需的转向角。

2.1预瞄距离的计算

KLf= 0.1         #look forward gain
Lf0 = 3.0       #look-ahead distance，偏置
#calculate Lf
Lf=KLf*v+Lf0

2.2 α的计算

由下图可以看出，

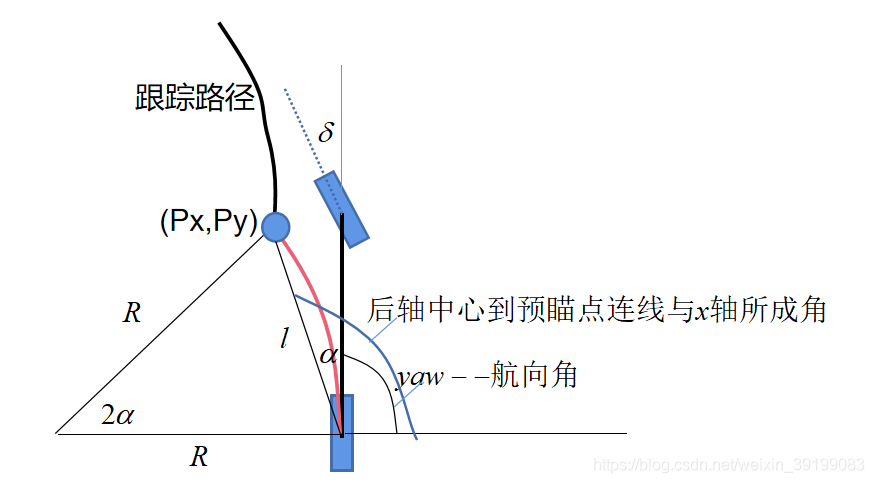
找到预瞄点后，直接用预瞄点和当前后轮中心计算连线与x轴所成角α_hat，然后α_hat减去航向角yaw即为α，代码如下

#计算alpha
            alpha_hat = math.atan2(target_y - y,target_x - x)
            alpha = alpha_hat - yaw

2.3 预瞄点的确定

预瞄点要为我们设定计算公式计算出的预瞄距离，刚好相等可能比较困难，预瞄点有可能落在最近时刻的一小段参考轨迹waypoints里的两个参考点之间，遍历最近时刻的参考点，直到第i个参考点与小车后轴中心的距离刚大于预瞄距离时，则取第i个点为近似预瞄点,代码如下：

#找Target
            for i in range(len(waypoints)):
                dx=self._current_x-waypoints[i][0]
                dy=self._current_y-waypoints[i][1]
                d = abs(math.sqrt(dx ** 2 + dy ** 2))
                if d>Lf:
                    target_x=waypoints[i][0]
                    target_y=waypoints[i][1]
                    break

3. Coursera Final Project说明

参见我另一篇博客

https://blog.csdn.net/weixin_39199083/article/details/116723353?spm=1001.2014.3001.5502   2.1小节 

4. 运行结果

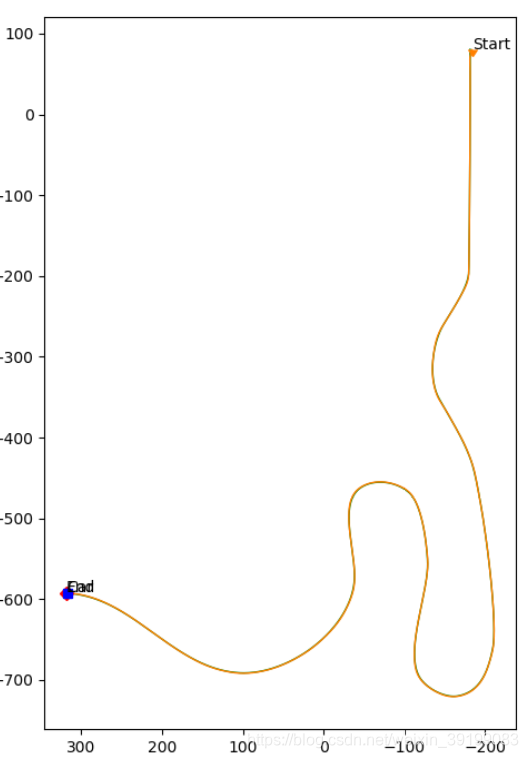
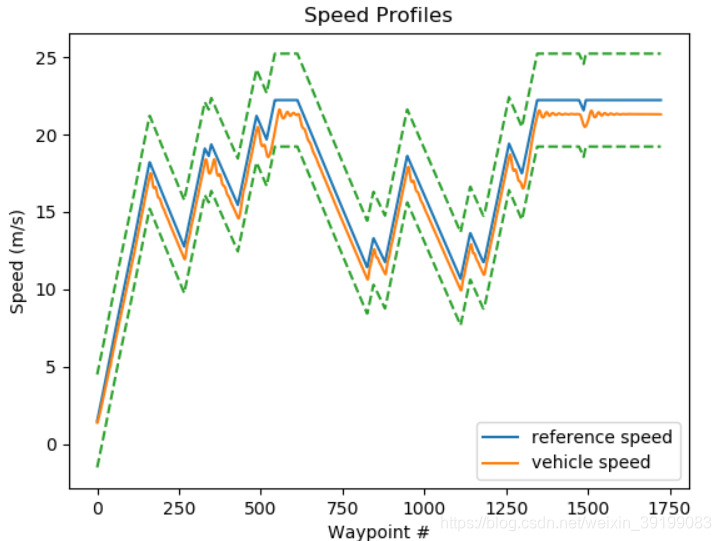
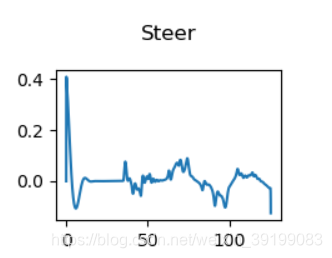
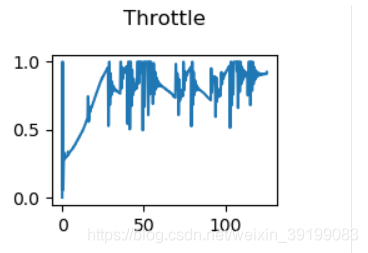
运行视频： https://www.bilibili.com/video/BV18y4y1g7aA

完整代码：https://download.csdn.net/download/weixin_39199083/18817439