系列文章目录

时空图神经网络1——GNN和GCN
时空图神经网络2——RNN和GRU
时序图神经网络3——T-GCN
时序图神经网络4——GAT

---

前言

本来我想学习STGCN，但是看到有博主提到由于当初时序卷积算法 WaveNet和 TCN 还未发表，空间依赖学习这条线上在当时确实也就切比雪夫GCN 和 GCN 比较能打，而随着 GAT、扩散图卷积、动态图卷积和GraphTransformer等技术的不断出现，空间依赖挖掘这上面的选择也越来越多，效果在当时还算不错，现在很多时空预测的论文都把该篇论文作为baseline（从【论文精读】STGCN-一种用于交通预测的时空图卷积网络这篇看到的）。
既然经常作为baseline，也是有学习的必要的，大家可以看这篇blog，我可能不再详细展开写。
也是这篇blog提醒我，我应该学习一下更先进的时序预测内容TCN和WaveNet。另外，之前有人给我推荐过 tsai 不知道用起来怎么样，GitHub 上有 5.6k Starred。

---

一、时域卷积网络 TCN

时域卷积网络（TCN，Temporal Convolutional Network）是基于 CNN 发展来的进行序列建模和预测的有价值的工具。CNN 通常与图像分类的任务相关，但是根据我个人对其原理的理解，我发现在处理序列数据的时候，一维卷积实际上完全能够提取到过去的信息。
关于 CNN 的原理，网上的讲解很多，我就不细讲了，讲清楚并写明白是一件很耗费时间的事情，我直接从 TCN 开始。

原文链接：An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling

1. TCN 简介

在 TCN 出现之前，深度学习背景下的序列建模主题主要与递归神经网络架构有关，如RNN、LSTM、GRU。在很多任务中发现，卷积网络可以取得比 RNNs 更好的性能，同时避免了递归模型的常见缺陷，如梯度爆炸/消失问题或缺乏内存保留。此外，卷积神经网络允许并行计算输出，这使得 TCN 在大规模数据上的训练和推理方面具有优势，能够更好地利用现代硬件的并行计算能力。TCN 可以通过堆叠多个卷积层来提取不同尺度的特征，这种多尺度信息提取能力使得 TCN 对序列数据中的局部依赖关系更加敏感。TCN 原文中提到，TCN 比 WaveNet 简单得多，没有跨层的跳跃连接、条件设定、上下文堆叠或门控激活。
TCN 的缺点是有限的建模能力：传统的卷积操作在局部感受野内工作，因此对于较长的序列建模和处理长期依赖关系，可能不如 RNN 表现好。但可以通过使用深层 TCN 和膨胀卷积等技术来扩大感受野。

2. TCN 原理

TCN 基于两个原则：一是网络产生与输入长度相同的输出；二是信息不能从未来泄漏到过去。

2.1 一维全卷积网络

为实现第一点，TCN 使用一维全卷积网络（FCN，fully-convolutional network ）架构，其中每个隐藏层的长度都与输入层相同，并且添加长度为 kernel_size - 1 的零填充，以确保后续层的长度与前一层相同。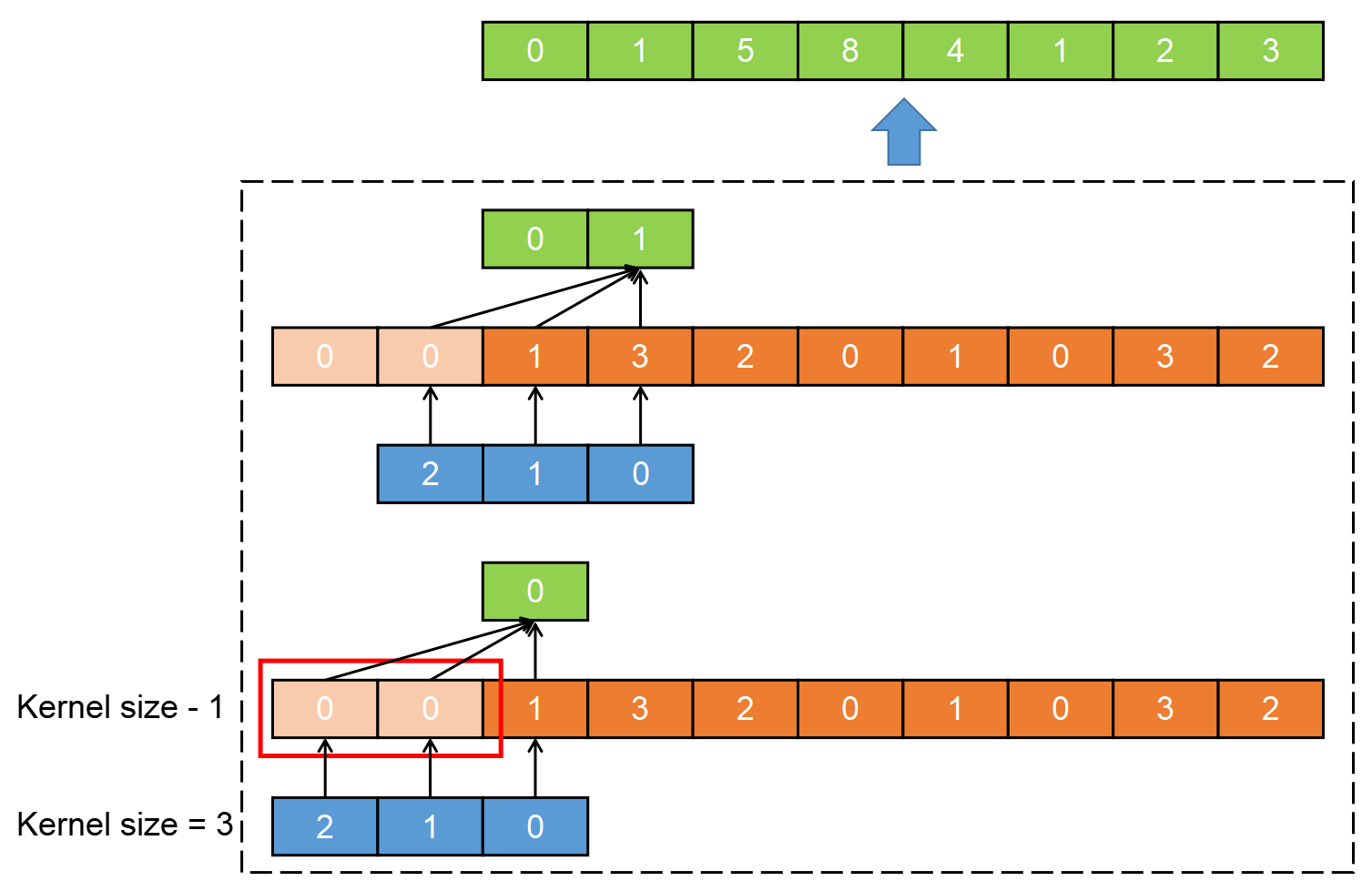

TCN 输入的尺寸是[batch_size, input_channels, seq_length]（在卷积中，num_channels 可以理解为 num_features），输出的尺寸是[batch_size, output_channels, seq_length]，与 torch.nn.conv1d 是一样的。上图是 num_channels=1 的情况。

2.2 因果卷积

为实现第二点，TCN 使用因果卷积（Causal Convolution），即某一时刻 t 的输出仅与前一层中时刻 t 及更早时刻的元素进行卷积，不允许未来时间的信息泄露。这其实很好理解也很好实现。上面的图中已经可以反映出因果卷积的特征。图中我已经将时间序列对其，可以清晰地看出，绿色的输出是通过卷积核与该位置以及之前的两个输入计算得到的。
而实现因果卷积跟只在左边填充 0 有关。一般情况下卷积是两头填充的，这样就会用到未来信息。下图的情况就是普通卷积，在这里是不行的。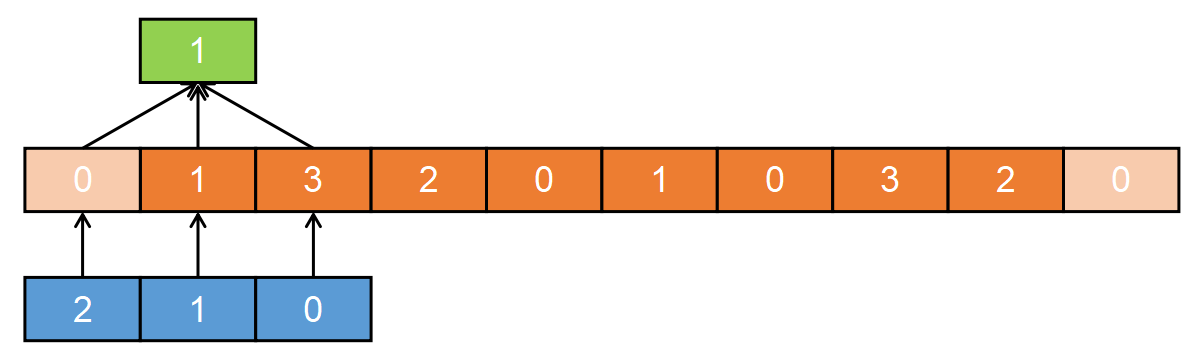

简而言之：TCN = 1D FCN + Causal CNN。
这种基本设计的一个主要缺点是，为了获得较长的有效历史长度，需要一个极深的网络或非常大的滤波器。因此，需要实现既具有深度又能拥有较长有效历史长度的网络。

2.3 膨胀卷积

采用膨胀卷积来解决这一问题，它能实现指数级扩大的感受野。膨胀因子由 dilations 参数给出。这有常见动图，膨胀因子为 [1, 2, 4, 8]，但是我不知道出自哪里，如果有人知道可以告诉我。

CNN 通过增加池化 pooling 层来获得更大的感受野，而经过 pooling 层后肯定存在信息损失的问题。膨胀卷积是在标准的卷积里注入空洞，以此来增加感受野。dilations 指的是 kernel 的间隔数量（标准的 CNN 中 dilatations 等于 1）。空洞的好处是不做 pooling 损失信息的情况下，增加了感受野，让每个卷积输出都包含较大范围的信息。
我们再看一维全卷积网络中的图（舍去了中间过程）：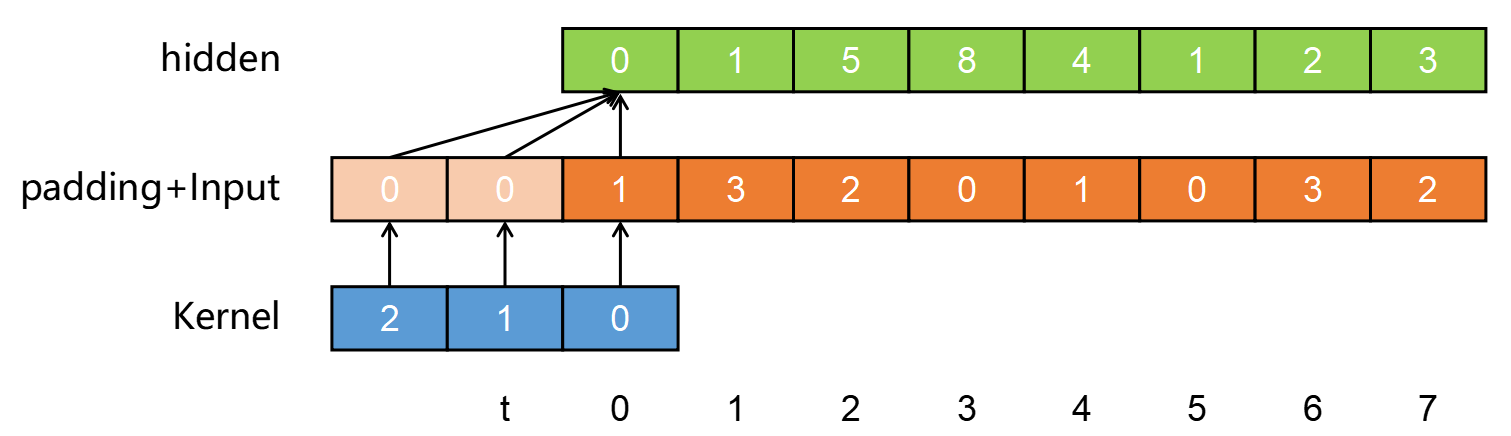

我们对橙色的输入进行一次一维卷积操作，此时 dilatations=1 ，我们得到绿色的隐藏层。我们可以看出 t=2 时刻的隐藏层数据是考虑到了[0, 3] 的输入数据，也就是[0, kernel_size]。那么，在 t=5 时刻的隐藏层数据，同样也是考虑到了[3, 6]的输入数据，这样看，我只需要知道隐藏层 t=2 和 t=5 时刻的数据，就相当于知道了输入层[0, 6]的信息了，此时 dilatations=3 。这样再看刚才的动图应该就更清晰了。

2.4 残差连接

整个模型深度仍然很深，为减少过深网络带来的梯度消失等问题，TCN 引入了和 ResNet 网络类似的残差块设计，将层与层之间的连接变成了残差结构。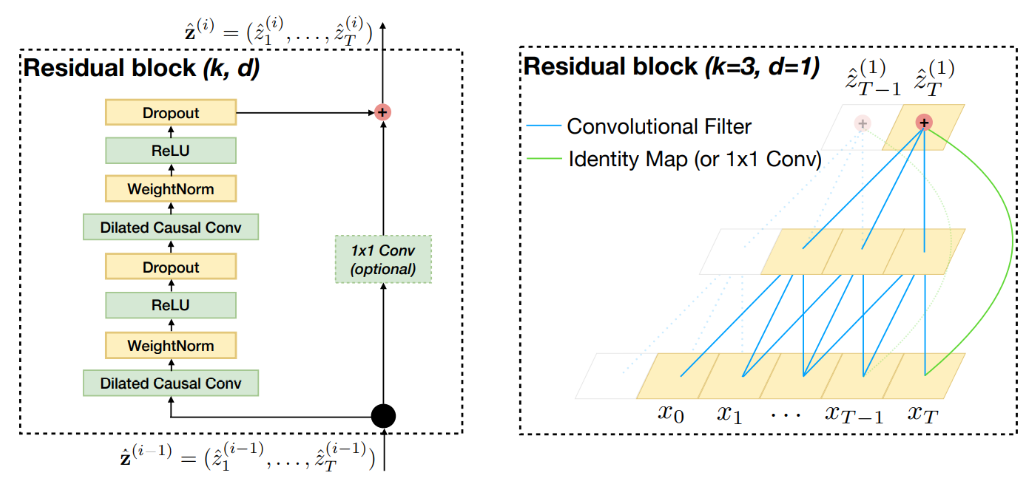

残差连接 skip connection 被证明是训练深层网络的有效方法，它使得网络可以以跨层的方式传递信息。本文构建了一个残差块来代替一层的卷积。如上图所示，一个残差块包含两层的卷积和非线性映射，在每层中还加入了 WeightNorm （规范化隐含层的输入，抵消梯度爆发的问题）和 Dropout （防止过拟合）来正则化网络。考虑到输入输出通道数可能不同，所以引入了一个 1×1 的卷积再做相加。
具体来说，在 TCN 的代码中，当输入通道数 n_inputs 与输出通道数 n_outputs 不匹配时，需要使用 1×1 卷积调整维度，使残差连接能够正确执行加法操作。

self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None

• 输入：形状为 [batch_size, n_inputs, sequence_length] 的特征图。
• 1×1 卷积：使用 n_outputs 个大小为 1 的卷积核，对每个时间步的特征进行线性组合。
• 输出：形状为 [batch_size, n_outputs, sequence_length] 的特征图，与主路径的输出维度一致，可直接相加。

2.5 参数选择

为了能更考虑到 sequence 中的所有信息，我们应该如何选择参数？
对于普通的一维卷积来说，如果 kernel_size=k，那经过 n 层以后的感受野是：$$l=1+n(k-1)$$反过来说，如果我的 seq_length=100，k=3，那么层数为：$$n=(100-1)/(3-1)=49.5$$向上取整得到 50。我们可以看到这样的层数确实很多。但是我们采用了膨胀卷积的方法。我们之前给出的例子中，膨胀因子是[1, 2, 4, 8]。一般情况下膨胀因子是指数增长的，在这里膨胀基准dilation_base=2，膨胀因子表示为：$d=b^i$，其中 b 是膨胀基准，d 是膨胀因子，i 是层数。感受野的大小为：$$l=1+\sum _{i=0}^{n-1}(k-1)\cdot b^i=1+(k-1)\cdot \frac{b^n-1}{b-1}$$我们令 k=3（跟之前一样），b=2。当 n=6 时：$$l=1+(3-1)\cdot \frac{2^6-1}{2-1}=126$$可以看出仅仅需要 6 层就远大于普通卷积 50 层的效果。根据上式求解 n，我们可以算出来需要的最小层数。此外，需要补充的 0 的个数 $p=b^i\cdot (k-1)$。
但是且慢！！！
我们这里的 n 指是层数但是跟本文不完全一样，本文中的层数指的是残差块的层数，看上面的图可以知道，每个残差块有两个卷积层，所以最后的视野实际上会是两倍：$$l=1+\sum _{i=0}^{n-1}(k-1)\cdot b^i=1+2\cdot (k-1)\cdot \frac{b^n-1}{b-1}$$

二、TCN 代码

TCN 分为两部分，TemporalBlock 和 TemporalConvNet ，前者是残差块，后者是 TCN 网络。代码中没有注释各个参数分别是什么让我这种初学者非常恼火，看起来很不方便。

1. TemporalConvNet

class TemporalConvNet(nn.Module):
    def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):
        super(TemporalConvNet, self).__init__()
        layers = []
        num_levels = len(num_channels)
        for i in range(num_levels):
            dilation_size = 2 ** i
            in_channels = num_inputs if i == 0 else num_channels[i-1]
            out_channels = num_channels[i]
            layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
                                     padding=(kernel_size-1) * dilation_size, dropout=dropout)]

        self.network = nn.Sequential(*layers)

    def forward(self, x):
        return self.network(x)

其中num_inputs 是 int，输入通道数（特征数）；num_channels 是 list ，每个 TemporalBlock 中隐藏层的 channels，就是每个残差连接之间两个卷积层的 channels，同时也是每个 block 输出的 channels；kernel_size 是 int，卷积核尺寸；dropout 是 float，代表随机失活率，防止过拟合。
代码很简洁，先对 num_channels 的个数进行循环（因为指定了每个 block 的 channel，所以个数就是 block 的个数），然后计算该 block 的 dilation，我们看到这里的 b=2。接下来是对输入每个 block 的通道数进行定义，当 i=0 也就是在第一个 block 的时候，设定为 in_channels，此时相应的 out_channels 是第 i 个 num_channels，刚才已经提到过了；当 i!=0 时，输入的通道数都是上一个输出层的通道数，也就是 num_channels[i-1]。通过这些参数搭建 TemporalBlock，再把每一层拼接起来，再通过 nn.sequential 就得到了完整的网络。

2. TemporalBlock

我们还是先看上面的代码，在构建网络的时候看入参我觉得更方便。
in_channel，out_channel，kernel_size 和 dilation 我们刚说完，stride 是 CNN 中的一个重要参数，代表卷积核在输入序列上滑动的步长，简单说，如果 kernel_size=3，我们第一次对输入序列进行运算的索引是[0, 1, 2]，第二次是[1, 2, 3]，但是如果 stride=2，第二次的就会变成 [2, 3, 4]，也就是说是跳过了一个位置。这样可以减少运算量，但是会使卷积后的尺寸变短，在 TCN 中要求尺寸保持一致，所以固定 stride=1。padding 是在序列最前面补充的 0 的个数，我们之前说过$p=b^i\cdot (k-1)$，这里也是一样的，作者已经写好了，不用我们自己计算。
参数讲完了我们再看代码：

class TemporalBlock(nn.Module):
    def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
        super(TemporalBlock, self).__init__()
        self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp1 = Chomp1d(padding)
        self.relu1 = nn.ReLU()
        self.dropout1 = nn.Dropout(dropout)

        self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp2 = Chomp1d(padding)
        self.relu2 = nn.ReLU()
        self.dropout2 = nn.Dropout(dropout)

        self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
                                 self.conv2, self.chomp2, self.relu2, self.dropout2)
        self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
        self.relu = nn.ReLU()
        self.init_weights()

    def init_weights(self):
        self.conv1.weight.data.normal_(0, 0.01)
        self.conv2.weight.data.normal_(0, 0.01)
        if self.downsample is not None:
            self.downsample.weight.data.normal_(0, 0.01)

    def forward(self, x):
        out = self.net(x)
        res = x if self.downsample is None else self.downsample(x)
        return self.relu(out + res)

好吧，没什么好看的，卷积 - 激活 - dropout重复了两次而已，再进行一次残差连接，跟前面图中所示完全一样。其中的 chomp 作用很简单，因为在 padding 的时候左右都会填充，在这里去掉右边的，代码如下：

class Chomp1d(nn.Module):
    def __init__(self, chomp_size):
        super(Chomp1d, self).__init__()
        self.chomp_size = chomp_size

    def forward(self, x):
        return x[:, :, :-self.chomp_size].contiguous()

总结

本文介绍了非 RNNs 的一种时序预测架构 TCN 的原理和代码，也许可以跟图神经网络结合，组成一个时序图神经网络。