图形学中的曲线通常与计算机图形、动画、几何建模等相关，用于表示物体的形状、路径或运动轨迹。与数学函数曲线相比，图形学中的曲线往往更侧重于实际应用，能够在数字模型中精确地描绘复杂的曲线和表面。

以下是图形学中常见的几种曲线类型及其总结：

1. 贝塞尔曲线（Bezier Curve）

• 形式: 由一组控制点定义，最常见的形式是二次和三次贝塞尔曲线。
  • 二次贝塞尔曲线：通过三个控制点定义。
  • 三次贝塞尔曲线：通过四个控制点定义。
• 特点: 用控制点来控制曲线的形状，广泛应用于矢量图形、字体设计、动画路径等。
• 图形: 曲线从一个点到另一个点，形状受控制点影响，常用于平滑的路径或曲面过渡。
• 公式（三次贝塞尔）: 

  

2. B样条曲线（B-Spline Curve）

• 形式: 由多个控制点和基函数定义的曲线，具有局部控制特性。
• 特点: 通过基函数加权控制点，常用于精确的多段曲线拟合，适用于复杂曲线的构建。相比贝塞尔曲线，B样条曲线有更好的控制能力，特别是在控制点的影响范围上。
• 图形: 平滑的曲线，通常用于多段拼接的曲线，广泛应用于3D建模中。
• 公式: 

3. NURBS曲线（Non-Uniform Rational B-Splines）

• 形式: NURBS是B样条曲线的扩展，允许控制点和基函数有不同的权重。
• 特点: 具有非常强的表达能力，可以表示常见的几何体（如圆、直线、自由曲面等）。NURBS可以处理更加复杂的形状，是工业设计、汽车、航空航天等领域的标准。
• 图形: 平滑的曲线，控制点与权重决定形状。
• 公式: 

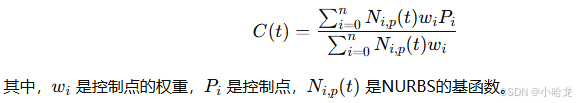
4. 样条曲线（Spline Curve）

• 形式: 样条曲线是一类通过一组控制点构建的平滑曲线，最常见的样条曲线是立方样条（Cubic Spline）。
• 特点: 样条曲线具有高平滑性，常用于插值与曲线拟合，广泛应用于数据可视化、动画和路径生成等。
• 图形: 曲线通过各控制点，具有平滑的连续性，且可以在多段区间内进行拟合。
• 公式: 常见的是立方样条，其每一段可以表示为一个三次多项式：

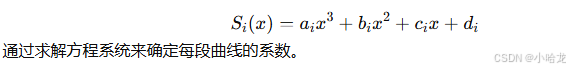
5. 圆弧（Arc）

• 形式: 圆弧是圆的一部分，通常由圆心、半径和起止角度来定义。
• 特点: 圆弧是非常基础的曲线，在计算机图形学中用于绘制圆形、弧形路径等。
• 图形: 圆弧段是圆的一部分，常用于绘制图标、界面元素等。
• 公式: 

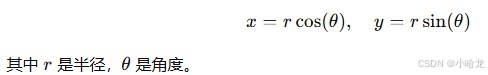
6. 赫尔姆霍兹曲线（Helmholtz Curve）

• 形式: 一种螺旋曲线，通常用于模拟绳索、弹簧等形状。
• 特点: 用于描述物体的螺旋路径，具有在三维空间中的复杂度。
• 图形: 螺旋形的曲线，通常应用于3D建模中。
• 公式: 

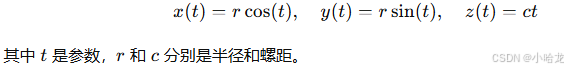
7. 圆锥曲线

• 形式: 包括圆、椭圆、双曲线、抛物线等。
• 特点: 这些曲线来源于圆锥面与平面交线的几何形状，常见于物理模拟、路径规划等。
• 图形:
  • 圆：所有点到圆心的距离相等。
  • 椭圆：点到两个焦点的距离和为常数。
  • 抛物线：焦点到任意点的距离等于点到导线的距离。
  • 双曲线：两条分支，焦点间距为常数。

8. Catmull-Rom曲线

• 形式: 一种插值曲线，通过一系列控制点生成平滑路径。
• 特点: 特别适用于动画路径生成和路径插值，具有局部控制特性。
• 图形: 平滑曲线通过控制点，常用于角色动画、物体移动路径等。
• 公式

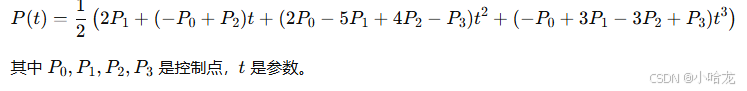
这些曲线是图形学中非常重要的工具，每种曲线都有其独特的用途，帮助我们在计算机图形、动画、建模等方面表现复杂的形状、路径和运动轨迹。