销售预测的方法与模型（六）-时间序列模型-ARIMA

可以看出效果还是非常显著的，ARIMA 模型是时间序列分析中最经典和广泛使用的模型之一，特别适用于那些没有明显季节性，但具有趋势和随机波动的时间序列。移动平均我们如何确定n，就是平均几个前面的值如何确定，我们也可以通过假设n值，再观察图形选取最合适的值。因为自变量并没有考虑其他维度数据，只考虑时间维度，我们可以使用前1季度（x1）和前2季度（x2）作为计算回归的因变量，计算预测值（y）。通过观察我

???? ??001

1090人浏览 · 2025-06-24 13:46:05

???? ??001 · 2025-06-24 13:46:05 发布

本篇将继续介绍基于时间序列分析的ARIMA模型，在这里温馨提示一下ARIMA本身包含回归预测的内容，如果对回归有疑问请查看前一篇关于回归的文章。

一、ARIMA介绍

ARIMA（AutoRegressive Integrated Moving Average，自回归积分滑动平均模型）是一种非常常用的时间序列分析模型，用来预测数据的未来趋势。它适用于平稳的、无季节性的时间序列。

1.1 ARIMA 模型的组成

ARIMA 模型的全称揭示了它的三个核心组成部分：

（1）AR (Auto-Regressive，自回归部分)：表示当前值与之前一段时间的值之间存在线性关系。通过使用过去的观测值预测当前值。

参数：p，自回归项的阶数。表示使用多少个前期的值来进行预测。

（2）I (Integrated，差分部分)：表示通过计算数据的差分，使非平稳时间序列变得平稳。即通过减去前一个时刻的值消除趋势。

参数：d，差分的次数。差分的目的是为了去除趋势成分，使数据平稳化。

（3）MA (Moving Average，移动平均部分)：表示当前值与过去的预测误差的线性组合。即将过去的预测误差纳入当前预测。

参数：q，移动平均项的阶数。表示使用多少个过去的预测误差来预测当前值。

因此，ARIMA 模型用符号 ARIMA(p,d,q)表示，分别代表自回归项（p）、差分次数（d）和移动平均项（q）的阶数。

1.2 ARIMA 模型的使用步骤

（1）时间序列平稳性检验：在应用 ARIMA 模型之前，必须确保数据是平稳的。如果数据有显著的趋势或波动，需要通过差分（I 部分）来平稳化。

（2）选择模型参数：通过分析自相关函数 (ACF) 和偏自相关函数 (PACF) 图，或者通过自动化工具（如 auto_arima），确定模型参数 p、d、q。

（3）模型拟合：使用历史数据来拟合 ARIMA 模型，估计模型中的参数。

（4）预测未来值：利用拟合好的模型进行未来的预测。

二、ARIMA例子

我们将通过一个例子来阐述这个模型的使用，并没有融入过多复杂的数学公式，如果大家对原理感兴趣，请自行翻阅其他资料。为了方便理解，我们直接使用excel手工计算，如果数据量较大的情况下，建议使用专业软件工具处理。

假设某一家企业6年每个季度的销售数据如下：

季度	销量
2018年1季度	4452
2018年2季度	4507
2018年3季度	5537
2018年4季度	8157
2019年1季度	6481
2019年2季度	6420
2019年3季度	7208
2019年4季度	9509
2020年1季度	6755
2020年2季度	6483
2020年3季度	7129
2020年4季度	9072
2021年1季度	7339
2021年2季度	7104
2021年3季度	7639
2021年4季度	9661
2022年1季度	7528
2022年2季度	7207
2022年3季度	7538
2022年4季度	9573
2023年1季度	7522
2023年2季度	7211
2023年3季度	7729
2023年4季度	9542

通过excel做图，我们可以观察到确实呈现出线性趋势，那么我们就可以利用回归进行数据分析预测：

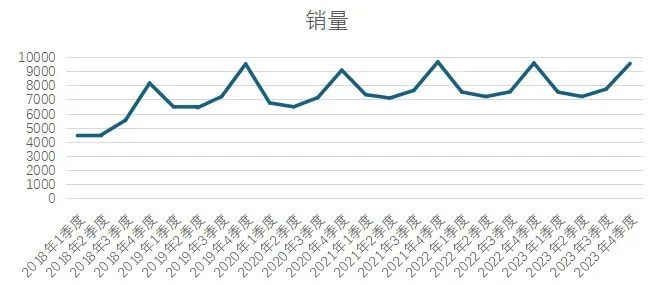
2.1 回归预测

因为自变量并没有考虑其他维度数据，只考虑时间维度，我们可以使用前1季度（x1）和前2季度（x2）作为计算回归的因变量，计算预测值（y）。

季度	销量	销量（前1季度）	销量（前2季度）
2018年1季度	4452
2018年2季度	4507
2018年3季度	5537	4507	4452
2018年4季度	8157	5537	4507
2019年1季度	6481	8157	5537
2019年2季度	6420	6481	8157
2019年3季度	7208	6420	6481
2019年4季度	9509	7208	6420
2020年1季度	6755	9509	7208
2020年2季度	6483	6755	9509
2020年3季度	7129	6483	6755
2020年4季度	9072	7129	6483
2021年1季度	7339	9072	7129
2021年2季度	7104	7339	9072
2021年3季度	7639	7104	7339
2021年4季度	9661	7639	7104
2022年1季度	7528	9661	7639
2022年2季度	7207	7528	9661
2022年3季度	7538	7207	7528
2022年4季度	9573	7538	7207
2023年1季度	7522	9573	7538
2023年2季度	7211	7522	9573
2023年3季度	7729	7211	7522
2023年4季度	9542	7729	7211

因为采用前1季度和前2季度，前面会有一些空白项。

公式：y = w * x1 + w * x2 + b。利用excel回归分析可以直接求解。

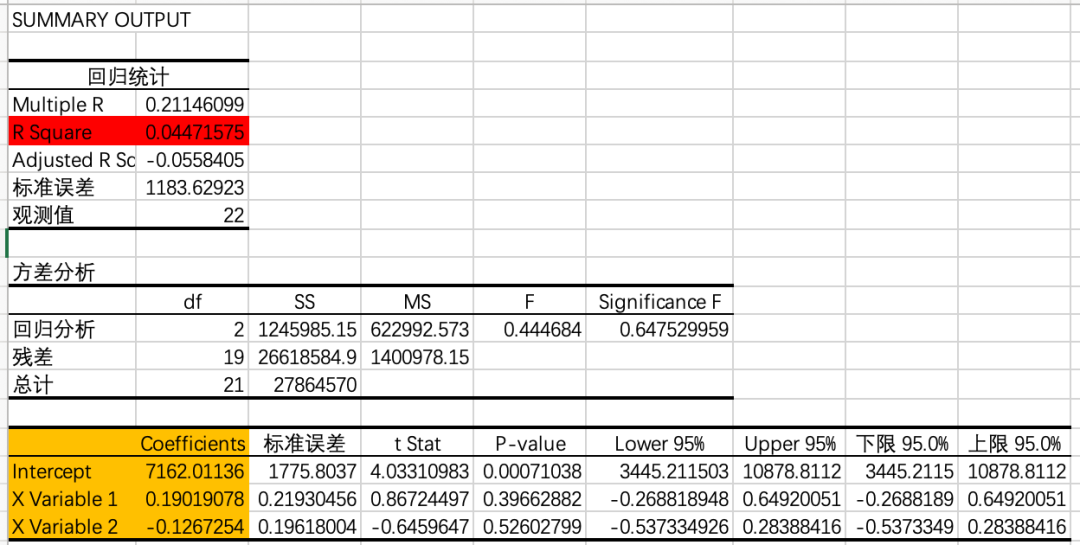
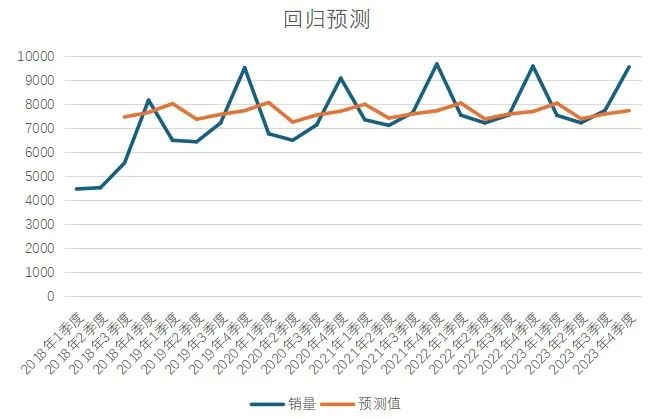
直接将截距和x1、x2带入公式，求得预测值，通过观察折线图和数据表可以发现预测值与实际值差距较大，效果并不理想，另外观察R²也可以看出效果确实差强人意，只有0.04（上面红色部分）。

季度	销量	销量（前1季度）	销量（前2季度）	预测值
2018年1季度	4452
2018年2季度	4507
2018年3季度	5537	4507	4452	7455.01981
2018年4季度	8157	5537	4507	7643.94642
2019年1季度	6481	8157	5537	8011.71913
2019年2季度	6420	6481	8157	7360.93888
2019年3季度	7208	6420	6481	7561.72898
2019年4季度	9509	7208	6420	7719.32956
2020年1季度	6755	9509	7208	8057.09895
2020年2季度	6483	6755	9509	7241.71844
2020年3季度	7129	6483	6755	7538.98824
2020年4季度	9072	7129	6483	7696.32079
2021年1季度	7339	9072	7129	7983.99688
2021年2季度	7104	7339	9072	7408.16884
2021年3季度	7639	7104	7339	7583.0891
2021年4季度	9661	7639	7104	7714.62163
2022年1季度	7528	9661	7639	8031.38931
2022年2季度	7207	7528	9661	7369.47365
2022年3季度	7538	7207	7528	7578.72765
2022年4季度	9573	7538	7207	7682.35965
2023年1季度	7522	9573	7538	8027.45178
2023年2季度	7211	7522	9573	7379.48434
2023年3季度	7729	7211	7522	7580.24877
2023年4季度	9542	7729	7211	7718.17918

2.2 差分处理

差分是时间序列分析中的一个重要概念，主要用于将非平稳序列转换为平稳序列，便于分析和建模。差分的基本思想是通过对时间序列数据做“减法”来消除趋势或季节性影响，从而使序列平稳化。

差分的主要目的是：

1. 消除趋势：在时间序列中，数据常常会随着时间的推移呈现出上升或下降的趋势。通过差分操作可以去除这一趋势，使数据更为平稳，便于建模。

2. 消除季节性波动：一些时间序列中存在周期性的波动，如按月、季度或年度重复出现的波动。差分能够消除这种季节性影响。

3. 让数据满足平稳性要求：很多时间序列模型（如ARIMA）假设输入数据是平稳的，而差分可以将不平稳数据转化为平稳数据。

4. 减少自相关性：差分也可以减少自相关性，特别是在ARIMA等模型中，自相关性过强会影响模型效果。

举例来说，比如一阶差分，就是用当前值减去上一个值。假设有一组数据1、2、3、4、5，可以看出他们是呈现出趋势性的，如果用一阶差分，就是2-1、3-2……依次类推，结果是每一个数之间都相差1，这样就可以消除趋势性。2阶只是对一阶差分后的序列再进行一次差分，消除曲线趋势或加速序列的平稳化。

上面的例子我们之间使用1阶差分做计算：

季度	销量	一阶差分
2018年1季度	4452
2018年2季度	4507	55
2018年3季度	5537	1030
2018年4季度	8157	2620
2019年1季度	6481	-1676
2019年2季度	6420	-61
2019年3季度	7208	788
2019年4季度	9509	2301
2020年1季度	6755	-2754
2020年2季度	6483	-272
2020年3季度	7129	646
2020年4季度	9072	1943
2021年1季度	7339	-1733
2021年2季度	7104	-235
2021年3季度	7639	535
2021年4季度	9661	2022
2022年1季度	7528	-2133
2022年2季度	7207	-321
2022年3季度	7538	331
2022年4季度	9573	2035
2023年1季度	7522	-2051
2023年2季度	7211	-311
2023年3季度	7729	518
2023年4季度	9542	1813

一阶差分之后，发现数据还是有季节性，那么我们给数据做移动平均消除季节性。移动平均我们如何确定n，就是平均几个前面的值如何确定，我们也可以通过假设n值，再观察图形选取最合适的值。

比如我们分别对n选取3、4、5，分别代表取3个季度平均、4个季度平均、5个季度平均，做表得到：

季度	销量	一阶差分	3个季度的移动平均	4个季度的移动平均	5个季度的移动平均
2018年1季度	4452
2018年2季度	4507	55
2018年3季度	5537	1030
2018年4季度	8157	2620	1235
2019年1季度	6481	-1676	658	507.25
2019年2季度	6420	-61	294.333333	478.25	393.6
2019年3季度	7208	788	-316.33333	417.75	540.2
2019年4季度	9509	2301	1009.33333	338	794.4
2020年1季度	6755	-2754	111.666667	68.5	-280.4
2020年2季度	6483	-272	-241.66667	15.75	0.4
2020年3季度	7129	646	-793.33333	-19.75	141.8
2020年4季度	9072	1943	772.333333	-109.25	372.8
2021年1季度	7339	-1733	285.333333	146	-434
2021年2季度	7104	-235	-8.3333333	155.25	69.8
2021年3季度	7639	535	-477.66667	127.5	231.2
2021年4季度	9661	2022	774	147.25	506.4
2022年1季度	7528	-2133	141.333333	47.25	-308.8
2022年2季度	7207	-321	-144	25.75	-26.4
2022年3季度	7538	331	-707.66667	-25.25	86.8
2022年4季度	9573	2035	681.666667	-22	386.8
2023年1季度	7522	-2051	105	-1.5	-427.8
2023年2季度	7211	-311	-109	1	-63.4
2023年3季度	7729	518	-614.66667	47.75	104.4
2023年4季度	9542	1813	673.333333	-7.75	400.8

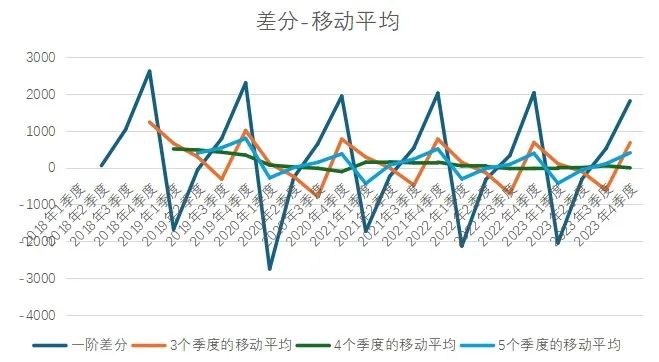
通过观察我们发现n=4，取4个季度的移动平均是最平稳的，那么我们就可以选择4个季度的移动平均参与后面的计算。

2.3 移动平均预测

我们继续使用回归计算移动平均后的预测值，此时x1=4个季度的移动平均（前1季），x2=4个季度的移动平均（前2季）：

季度	4个季度的移动平均	4个季度的移动平均（前1季）	4个季度的移动平均（前2季）	移动平均预测值
2018年1季度
2018年2季度
2018年3季度
2018年4季度
2019年1季度	507.25
2019年2季度	478.25
2019年3季度	417.75	478.25	507.25	317.08369
2019年4季度	338	417.75	478.25	275.204501
2020年1季度	68.5	338	417.75	222.056545
2020年2季度	15.75	68.5	338	30.9397831
2020年3季度	-19.75	15.75	68.5	16.9735078
2020年4季度	-109.25	-19.75	15.75	-4.3009794
2021年1季度	146	-109.25	-19.75	-66.937804
2021年2季度	155.25	146	-109.25	129.310946
2021年3季度	127.5	155.25	146	112.55625
2021年4季度	147.25	127.5	155.25	91.265019
2022年1季度	47.25	147.25	127.5	108.372544
2022年2季度	25.75	47.25	147.25	32.9015291
2022年3季度	-25.25	25.75	47.25	26.3002593
2022年4季度	-22	-25.25	25.75	-9.2748869
2023年1季度	-1.5	-22	-25.25	-2.1725411
2023年2季度	1	-1.5	-22	12.6251274
2023年3季度	47.75	1	-1.5	12.5735615
2023年4季度	-7.75	47.75	1	46.772948

可以观察到R²已经从简单回归预测的不到0.1上升到0.6了（上面红色部分），效果非常显著。

2.4 ARIMA预测

首先，我们把实际数据、一阶差分、移动平均的预测值整理为一张数据表：

季度	销量	一阶差分	移动平均预测值
2018年1季度	4452
2018年2季度	4507	55
2018年3季度	5537	1030
2018年4季度	8157	2620
2019年1季度	6481	-1676
2019年2季度	6420	-61
2019年3季度	7208	788	317.08369
2019年4季度	9509	2301	275.204501
2020年1季度	6755	-2754	222.056545
2020年2季度	6483	-272	30.9397831
2020年3季度	7129	646	16.9735078
2020年4季度	9072	1943	-4.3009794
2021年1季度	7339	-1733	-66.937804
2021年2季度	7104	-235	129.310946
2021年3季度	7639	535	112.55625
2021年4季度	9661	2022	91.265019
2022年1季度	7528	-2133	108.372544
2022年2季度	7207	-321	32.9015291
2022年3季度	7538	331	26.3002593
2022年4季度	9573	2035	-9.2748869
2023年1季度	7522	-2051	-2.1725411
2023年2季度	7211	-311	12.6251274
2023年3季度	7729	518	12.5735615
2023年4季度	9542	1813	46.772948

其次，计算基于一阶差分的预测值和销量预测值。那么

·一阶差分的预测值=移动平均预测值*n（n=4季度）-前3季度差分预测值的和

·销售预测值=一阶差分的预测值+前一季度的销售预测值

计算结果如下表：

季度	销量	一阶差分	移动平均预测值	一阶差分预测值	销量预测值（ARIMA）
2018年1季度	4452				4452
2018年2季度	4507	55		55	4507
2018年3季度	5537	1030		1030	5537
2018年4季度	8157	2620		2620	8157
2019年1季度	6481	-1676		-1676	6481
2019年2季度	6420	-61		-61	6420
2019年3季度	7208	788	317.08369	385.33476	6805.33476
2019年4季度	9509	2301	275.204501	2452.48325	9257.81801
2020年1季度	6755	-2754	222.056545	-1888.5918	7369.22618
2020年2季度	6483	-272	30.9397831	-825.46705	6543.75913
2020年3季度	7129	646	16.9735078	329.469659	6873.22879
2020年4季度	9072	1943	-4.3009794	2367.3853	9240.61409
2021年1季度	7339	-1733	-66.937804	-2139.1391	7101.47496
2021年2季度	7104	-235	129.310946	-40.472046	7061.00292
2021年3季度	7639	535	112.55625	262.450874	7323.45379
2021年4季度	9661	2022	91.265019	2282.22037	9605.67416
2022年1季度	7528	-2133	108.372544	-2070.709	7534.96514
2022年2季度	7207	-321	32.9015291	-342.35611	7192.60903
2022年3季度	7538	331	26.3002593	236.045794	7428.65483
2022年4季度	9573	2035	-9.2748869	2139.91979	9568.57462
2023年1季度	7522	-2051	-2.1725411	-2042.2996	7526.27497
2023年2季度	7211	-311	12.6251274	-283.16543	7243.10954
2023年3季度	7729	518	12.5735615	235.839531	7478.94907
2023年4季度	9542	1813	46.772948	2276.71733	9755.66641

最后，我们对比一下普通回归预测和用ARIMA预测的差距。

季度	销量	销量预测值（ARIMA）	预测值（回归）
2018年1季度	4452	4452
2018年2季度	4507	4507
2018年3季度	5537	5537	7455.01981
2018年4季度	8157	8157	7643.94642
2019年1季度	6481	6481	8011.71913
2019年2季度	6420	6420	7360.93888
2019年3季度	7208	6805.33476	7561.72898
2019年4季度	9509	9257.81801	7719.32956
2020年1季度	6755	7369.22618	8057.09895
2020年2季度	6483	6543.75913	7241.71844
2020年3季度	7129	6873.22879	7538.98824
2020年4季度	9072	9240.61409	7696.32079
2021年1季度	7339	7101.47496	7983.99688
2021年2季度	7104	7061.00292	7408.16884
2021年3季度	7639	7323.45379	7583.0891
2021年4季度	9661	9605.67416	7714.62163
2022年1季度	7528	7534.96514	8031.38931
2022年2季度	7207	7192.60903	7369.47365
2022年3季度	7538	7428.65483	7578.72765
2022年4季度	9573	9568.57462	7682.35965
2023年1季度	7522	7526.27497	8027.45178
2023年2季度	7211	7243.10954	7379.48434
2023年3季度	7729	7478.94907	7580.24877
2023年4季度	9542	9755.66641	7718.17918

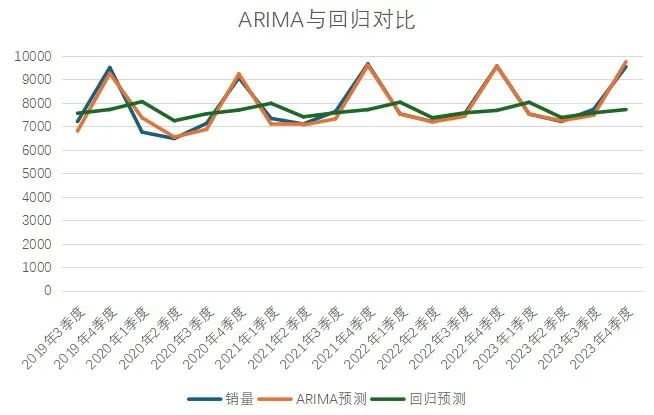
可以看出效果还是非常显著的，ARIMA 模型是时间序列分析中最经典和广泛使用的模型之一，特别适用于那些没有明显季节性，但具有趋势和随机波动的时间序列。它通过自回归、差分和平滑误差来建模时间序列的变化，从而为未来的值提供准确的预测。其他的基于ARIMA的模型请大家自行研究或者和我们联系沟通，基本思路还是通过加入季节性等其他维度进行数据处理，比如SARIMA等。

小结：ARIMA适用场景

· 产品销量预测（如零售商品、线上订单）

· 财务指标预测（如销售额、利润）

· 需求和供应链管理中的预测

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐