原文地址

Highlights

本文引入“容量密度”的概念来评价大型语言模型（LLM）的训练质量，并描述了兼顾有效性和效率的LLM的发展趋势。

（相对）容量密度。对于给定的LLMM，其容量密度定义为有效参数大小与实际参数大小之比，其中有效参数大小是参考模型达到M性能所需的最小参数数。

我们揭示了自2023年以来发布的开源基础LLM容量密度的经验规律。

Densing Law。LLM的最大容量密度随时间呈指数增长趋势。
$ln(p_{max})=At+B$
这里，$p_{max}$是在时间t处的LLM的最大容量密度。

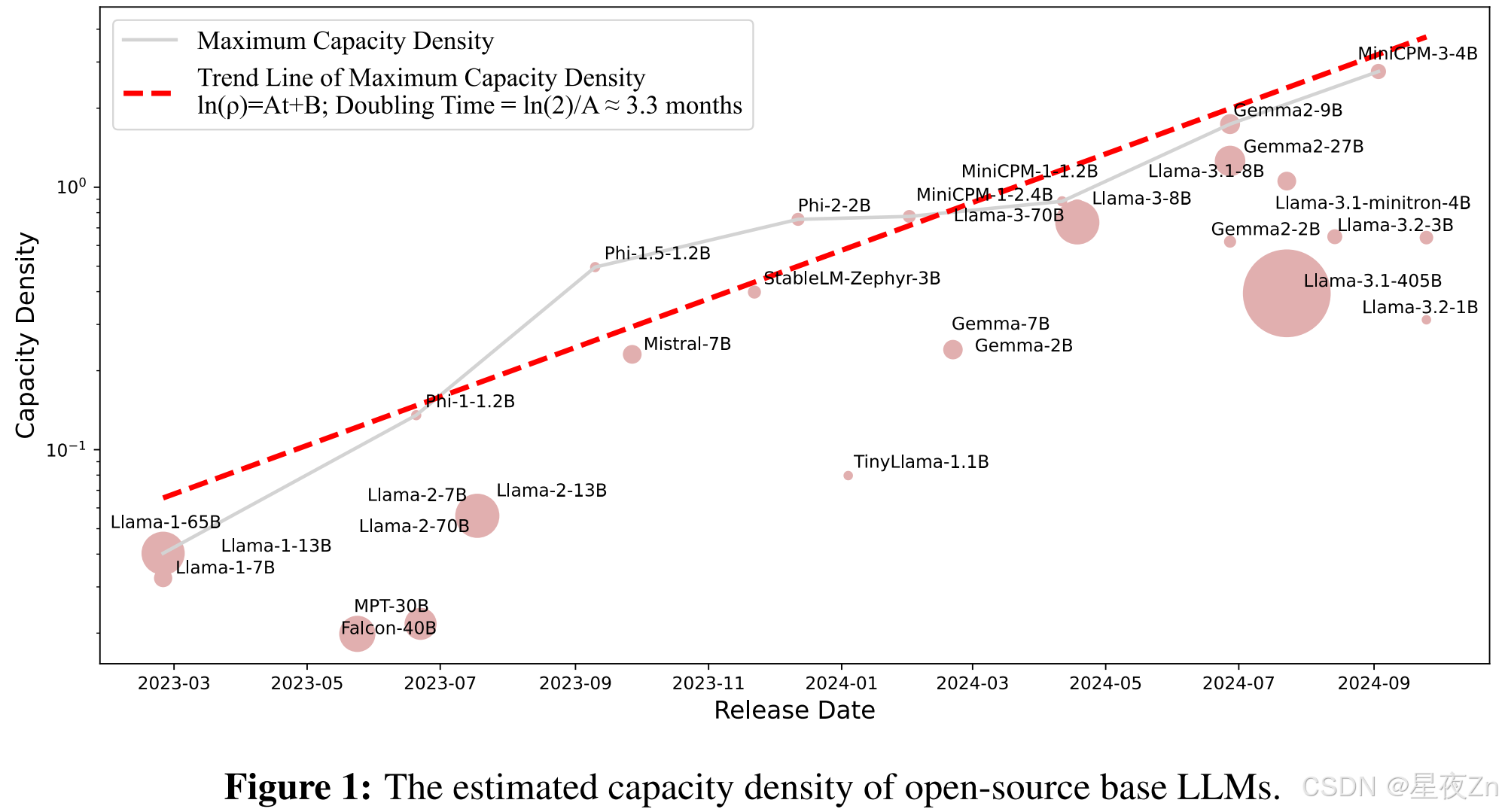
图1显示了流行LLM的容量密度，通过其在5个广泛使用的基准测试中的性能来衡量。最大容量密度与发布日期之间拟合出趋势，显示A ≈ 0.007，$R^2$ ≈ 0.93。这表明LLM的最大容量密度大约每3.3个月增加一倍。容量密度增长率受特定评估基准和参考模型的影响。换句话说，大约三个月，使用参数大小为一半的模型，可以实现与当前最先进的LLM相当的性能。

Abstract

大型语言模型（LLM）已经成为人工智能领域的一个里程碑，其性能可以随着模型大小的增加而提高。然而，这种扩展给训练和推理效率带来了巨大的挑战，特别是对于在资源受限的环境中部署LLM，并且扩展趋势变得越来越不可持续。本文介绍了“容量密度”的概念，作为一个新的度量标准，以评估质量的LLM在不同的规模和描述的趋势LLM的有效性和效率。为了计算给定目标LLM的容量密度，我们首先引入一组参考模型，并根据这些参考模型的参数大小开发一个标度律来预测这些参考模型的下游性能。然后，我们将目标LLM的有效参数大小定义为参考模型实现等效性能所需的参数大小，并将容量密度形式化为目标LLM的有效参数大小与实际参数大小的比率。容量密度为评估模型有效性和效率提供了一个统一的框架。我们对最近的开源基础LLM的进一步分析揭示了一个经验定律（密度定律），即LLM的容量密度随时间呈指数级增长。更具体地说，使用一些广泛使用的基准进行评估，LLM的容量密度大约每三个月就会翻一番。该法律提供了新的视角来指导未来的LLM发展，强调了提高容量密度的重要性，以最小的计算开销实现最佳结果。

1 Introduction

近年来，大型语言模型（LLM）在人工智能领域中引起了极大的关注，在各种任务中表现出了显著的改进（Bommasani等人，2021年; Qiu等人，2020年; Han等人，2021年; Touvron等人，2023年a;开放人工智能，2023年）。LLM的标度律进一步揭示了模型性能随着模型参数和训练数据的增加而持续改善（Kaplan等人，2020年; Henighan等人，2020年; Hoffmann等人，2022年）的报告。这一发现导致了具有数千亿个参数的LLM的发展，例如GPT-3 175 B（Brown等人，2020）、PaLM 540 B（乔杜里等人，2023），和美洲驼-3.1-405B（Dubey等人，2024年），在更广泛的应用中表现出卓越的能力。

此外，随着LLM的发展，提高推理效率变得越来越迫切：1）随着LLM部署在不断扩大的场景阵列中，推理成本已经超过了训练成本，成为实际应用中的主要瓶颈（Sardana等人，2024年; Yun等人，2024年;开放人工智能，2024 a）。2)越来越需要在资源受限的终端设备（如智能手机）上部署LLM，用作个人助理，这要求模型更加高效和紧凑（Gunter等人，2024; Xue等人，2024年; Hu等人，2024年）的报告。3)推理缩放定律表明允许LLM在推理阶段生成更多的用于“思考”的标记对于提高复杂推理任务中的性能是至关重要的（Brown等人，2024年;开放人工智能，2024 b;斯内尔等人，2024），进一步增加了对高效推理的需求。为了应对这些挑战，许多努力致力于开发仅具有数十亿个参数的高效LLM，以减少推理开销，例如OpenAI的GPT-4 o-mini（OpenAI，2024 a）和Apple的Apple Intelligence（Gunter等人，2024年）的报告。

考虑到这两条看似矛盾的路径–提高LLM的有效性与降低LLM的效率–自然会产生这样的问题：我们能否定量评估不同尺度的LLM的质量？是否有一个反映LLM效率趋势的定律，就像标度定律对参数和数据标度所做的那样？

为此，我们引入了容量密度的概念，它可以作为评估和比较各种规模的LLM训练质量的指标。准确衡量LLM的能力，或其智能水平的各个方面，是相当具有挑战性的。在本文中，我们设计了一种方法来评估相对容量密度2。具体来说，我们使用一个参考模型，然后估计其下游任务的性能和参数大小之间的缩放函数。基于尺度函数，对于任何给定的模型，我们计算其有效参数大小-参考模型实现等效性能所需的参数数量。LLM相对于参考模型的密度被定义为其有效参数大小与其实际参数大小的比率。通过引入模型密度的概念，我们的目标是更准确地衡量模型质量，并实现不同尺度模型之间的比较。这种评估方法有可能为LLM发展的未来方向提供新的见解，帮助研究人员找到有效性和效率之间的最佳平衡。

1.1 Key Findings

在定义了LLM密度之后，我们分析了近年来广泛使用的29个开源预训练基础模型。我们对模型密度的主要发现是：

Densing Law。LLM的最大容量密度随时间呈指数增长趋势。
$$ln(p_{max})=At+B$$
这里，$p_{max}$是在时间t处的LLM的最大容量密度。

基于我们对5个广泛使用的基准测试的评估，MMLU（Hendrycks等人，2020）、BBH（Suzgun等人，2023）、MATH（Hendrycks等人，2021）、人类评价（Chen等人，2021）和MBPP（Austin等人，2021年），A = 0.007，这意味着LLM的最大密度大约每三个月翻一番。例如，2024年2月1日发布的MiniCPM-1- 2.4 B可以实现与2023年9月27日发布的Mistral-7 B相当甚至上级的性能。我们可以使用只有35%参数的LLM在4个月后获得大致相同的性能。值得注意的是，使用不同的评估基准可能会导致模型密度的估计和增长率略有变化。我们鼓励社会各界制定更全面的评估基准，以确保更准确地测量密度。

基于大语言模型（LLMs）密度呈现出持续以指数趋势增长的结论，我们可以进一步推导出以下含义：

推论1.推理成本呈指数级下降：对于具有同等下游性能的LLM，推理成本呈指数级下降。

密度定律表明有效参数大小与真实的参数大小的比率大约每三个月翻一番。直观地说，在三个月内，我们可以使用只有一半参数的模型实现与当前最先进模型相当的性能。因此，对于等效的下游性能，推理成本呈指数下降。我们发现，从2023年1月至今，GPT-3.5级别模型的推理成本下降了266.7倍。

推论2.稠密定律×摩尔定律：在相同面积的芯片上运行的线性激光器的有效参数大小呈指数增长。

摩尔定律（摩尔，1965）指出，集成在相同面积的芯片上的电路数量呈指数级增加。这意味着计算能力的指数级增长。密度定律表明，LLM的密度每3.3个月翻一番。结合这两个因素，我们可以得出结论，可以在相同价格的芯片上运行的LLM的有效参数大小的增加速度快于LLM的密度和芯片的计算能力。

推论3.ChatGPT释放后密度增长加速：随着ChatGPT的释放，LLM密度的增长速度增加了50%。

我们比较了ChatGPT发布前后LLM密度的增长趋势。结果表明，发布ChatGPT模型后，最大密度的增长速度明显加快。具体而言，ChatGPT发布后，LLM密度增长率提升了50%。

推论4. 高效压缩 $!=$ 密度提高：现有的剪枝和蒸馏方法通常不能产生具有更高密度的高效LLM。

为了提高模型推理的效率，许多研究者致力于一系列的模型压缩算法，例如剪枝和蒸馏（Ma等人，2023年; Sun等人，2024年; Yang等人，2024年; Xu等人，2024年）的报告。这些算法通常被认为改善了所得到的压缩模型的性能。然而，通过比较一些模型与它们的压缩对应物，我们可以观察到广泛使用的剪枝和蒸馏方法通常导致比原始模型更小的模型和更低的密度。我们鼓励社区进一步探索更有效的模型压缩算法，重点关注提高更小模型的密度。

推论5. Towards Density-Optimal Training - Green Scaling Law：学习型学习者的发展应该从以成绩为中心转向以密度为中心。

密度是反映有效性和效率之间的权衡的度量。因此，盲目地增加模型参数来追求性能的提高会导致模型密度降低，从而造成不必要的能量消耗。例如，虽然美洲驼-3.1-405 B（Dubey等人，2024）在开源模型中实现了最先进的性能，它需要的计算资源是其他模型的数百倍。因此，模型开发人员需要将重点从仅仅优化性能转移到优化密度上。这种方法旨在以最小的计算成本获得最佳结果，从而实现更可持续和环境友好的标度律。

在这项工作中，我们提出了一个新的评价指标，密度，LLM，它可以提供一个新的，统一的角度对当前的两个趋势-提高有效性和提高效率。基于我们提出的度量标准，我们评估了29个开源模型，并发现了一个经验法则，命名为Densing法则：LLM的密度呈指数增长趋势。基于这种经验关系，我们讨论了几个推论并提供了观察证据。通过这一新颖的评价视角，我们希望为LLM的未来发展提供有价值的见解和指导。

2 Density for Large Language Models

在本节中，我们正式定义了LLM的密度，其计算为有效参数大小与实际参数大小的比值。在接下来的章节中，我们将首先描述LLM密度的总体框架和正式定义。然后介绍了如何利用标度律估计有效参数的大小。

2.1 Overall Framework and Definition

该分数可以通过各种指标计算，具体取决于下游任务，例如准确率、F1分数等。为了计算有效参数规模，我们训练一系列具有不同参数规模和训练数据的参考模型。基于这些模型，我们拟合参数规模与性能之间的函数：$S=f(N)$，其中$S$表示下游性能，$N$表示参考模型的参数规模。然后我们可以计算有效参数规模为$\hat{N}(S)=f^{-1}(S)$，并且$\mathcal{M}$的密度定义为：

$$\rho (\mathcal{M})=\frac{\hat{N}(S_{\mathcal{M}})}{N_{\mathcal{M}}}=\frac{f^{-1}(S_{\mathcal{M}})}{N_{\mathcal{M}}}$$

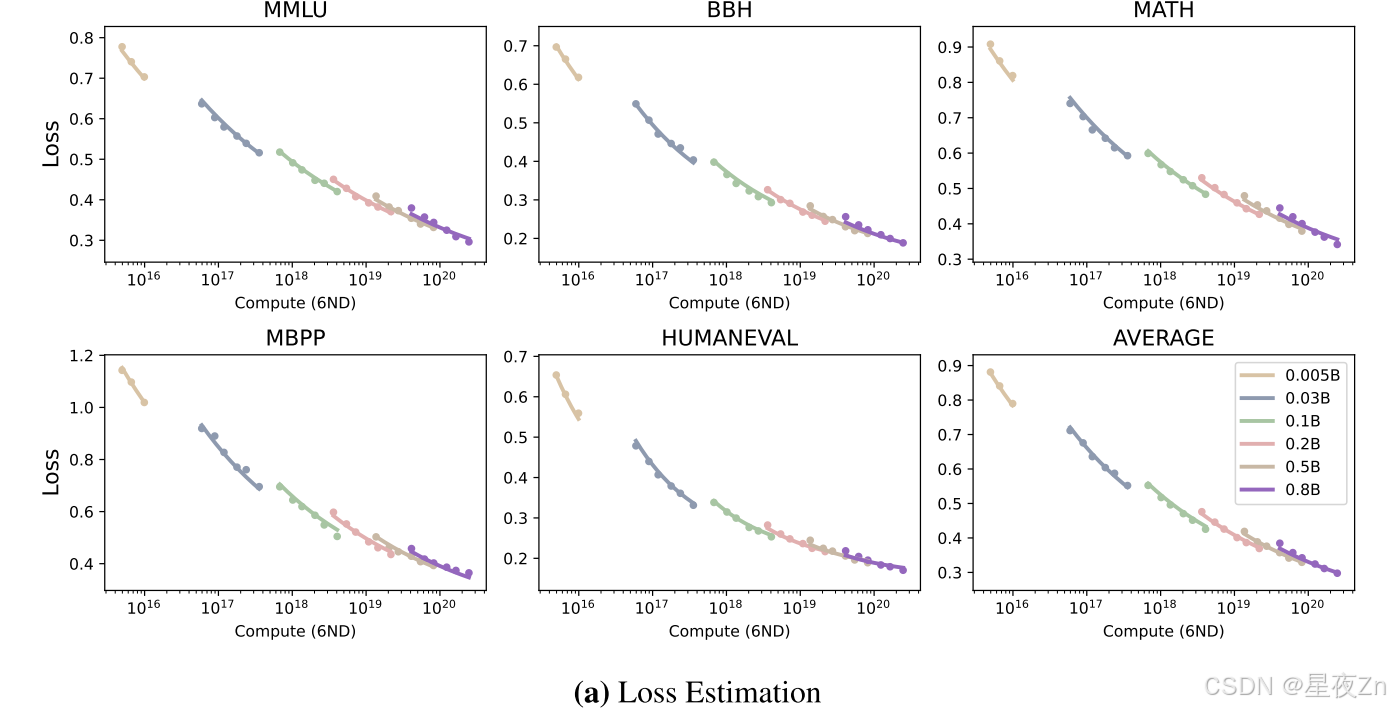
需要注意的是，缩放定律通常用于拟合语言建模损失与参数规模之间的关系（Kaplan et al., 2020），直接预测下游任务性能并非易事。受Llama-3（Dubey et al., 2024）的启发，我们采用两步估计方法：（1）损失估计：在第一步中，我们使用一系列参考模型来拟合测试集上参数规模与语言建模损失之间的关系，表示为 $\mathcal{L}=f_1(N)$。（2）性能估计：由于存在新兴能力（Wei et al., 2022a），使用训练计算有限的参考模型准确估计参数规模与性能之间的关系具有挑战性。因此，我们采用开源模型来计算它们在测试集上的损失和性能，并拟合关系 $s=f_2(\mathcal{L})$。这种两步估计过程使我们能够推导出 $s=f_2(f_1(N))$。在接下来的部分中，我们将详细描述 $f_1(\cdot )$ 和 $f_2(\cdot )$ 的拟合过程。

2.2 Loss Estimation

为了预测下游任务的性能，第一步是使用广泛用于LLM预训练的缩放定律来拟合参数规模与语言模型损失之间的函数。之前的缩放定律主要关注整个序列的语言模型损失，这反映了模型估计给定语料库概率的能力。然而，下游任务中的实例通常包括输入指令和输出答案，我们主要关注输出答案的概率。因此，在本工作中，我们专注于拟合条件损失 $\mathcal{L}=-\log (P(\text{answer}\mid \text{instruction}))$。具体而言，我们估计条件损失 $\mathcal{L}$、参数规模 $N$ 以及训练令牌数量 $D$ 之间的幂律函数：

$$\mathcal{L}=a{N}^{-\alpha }+b{D}^{-\beta },$$

其中 $a$、$\alpha$、$b$ 和 $\beta$ 是需要拟合的参数。

在先前关于标度定律的研究中（Kaplan等人，2020），通常需要在验证语料库上指定损失，并且在该语料库中的所有令牌上计算平均损失。在这项工作中，我们的目标是使模型的性能适合下游任务，这需要模型根据输入指令输出答案。因此，我们直接计算下游任务的条件损失，这意味着模型在给定任务输入的情况下生成答案时所产生的损失。(1)对于多项选择题，仅根据正确选项的内容计算损失可能会导致不准确的估计，因为它忽略了不正确选项的内容。此外，如果我们只计算最终选项标签上的损失，单个令牌的损失也不稳定。因此，我们将问题及其多个选项连接起来作为输入，输出是对输入问题的分析以及最终答案标签。(2)对于大多数复杂的问题，例如数学问题，我们通常需要模型在提供最终答案之前生成一系列推理步骤。对于这些任务，在计算损失时，我们将推理步骤和正确答案作为输出来计算模型的损失。值得注意的是，大多数数据集并不为每个实例提供推理步骤。对于这两种类型的任务，我们使用GPT-4 o（OpenAI，2023）为所有测试实例生成推理步骤。这些方法使我们能够通过考虑不同任务的特定要求和格式来更好地估计模型的性能。

2.3 Performance Estimation

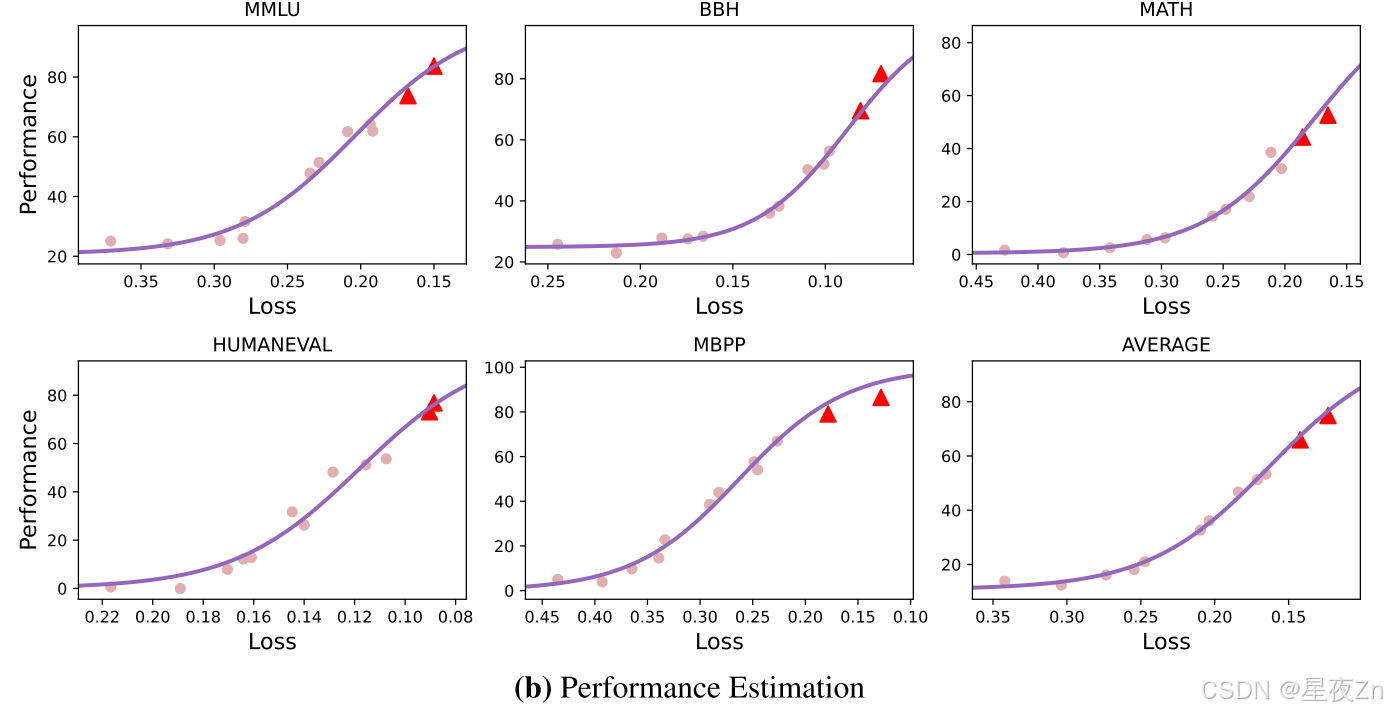
在第二步中，我们需要根据测试集上的损失来预测下游任务的性能。在损失估计步骤中，使用有限训练计算训练的标度律模型通常无法在下游任务上获得有意义的分数，大多数标度律模型仅在随机猜测的水平上执行。因此，仅用这些模型是不可能预测下游性能的。为了解决这个问题，我们将经过良好训练的开源模型用于函数拟合，并计算它们在测试集上的损失和性能。考虑到大多数下游任务的性能是有界的，我们使用sigmoid函数进行拟合。sigmoid函数自然地将所有输入值映射到0到1的范围。此外，当损失特别大时，模型的性能应该接近随机猜测，当损失特别小时，模型的性能应该接近上界。这个特性与sigmoid函数的特性一致，sigmoid函数在曲线的两端都非常平坦。具体而言，我们使用以下函数估计下游性能：

$$S=\frac{c}{1+e^{-\gamma (\mathcal{L}-l)}}+d,$$

其中$c$、$\gamma$、$l$和$d$是需要估计的参数。

2.4 Density

在拟合公式2和公式3后，给定模型$\mathcal{M}$的性能$S_{\mathcal{M}}$，我们可以通过利用这些公式的逆函数来推断有效参数规模。需要注意的是，在公式2中，损失$\mathcal{L}$是参数数量$\hat{N}$和训练数据规模$D$的双变量函数。因此，在计算有效参数规模时，需要指定特定的训练数据规模$D$。这里，为了计算有效参数规模，我们默认使用$D=D_0=1T$令牌。然后，有效参数规模可以解释为参考模型在使用$D_0$令牌训练时需要的参数规模，以达到等效性能。具体而言，我们可以计算有效参数规模如下：

$$\hat{\mathcal{L}}(S_{\mathcal{M}})=l-\frac{1}{\gamma }\ln \left(\frac{c}{S_{\mathcal{M}}-d}-1\right);\hat{N}(S_{\mathcal{M}})={\left(\frac{\hat{\mathcal{L}}(S_{\mathcal{M}})-b{D}_0^{-\beta }}{a}\right)}^{-\frac{1}{\alpha }}.$$

现在，我们已经建立了下游性能与有效参数规模之间的关系。给定模型$\mathcal{M}$的密度为$\rho (\mathcal{M})=\frac{\hat{N}(S_{\mathcal{M}})}{N_{\mathcal{M}}}$。直观上，如果一个模型能够在相同参数规模下实现更好的性能，则该模型的密度更高。因此，在未来，考虑到部署设备的有限计算资源，我们应该致力于提高模型的密度，而不仅仅是增加模型参数规模以获得更好的性能。

3 Density Evolution

3.1 Evaluation Settings

Dataset
在这项工作中，我们采用了以下广泛使用的数据集进行评估：MMLU（Hendrycks等人，2020），BBH（Suzgun等人，2023）用于挑战性的逻辑推理任务，MATH（Hendrycks等人，2021）和HumanEval（Chen等人，2021）、MBPP（奥斯汀等人，2021）进行编码任务。我们应用开源工具（OpenCompass，2023; Liu等人，2024年）进行评价。在此，我们以少次上下文学习的方式对所有模型进行评估，这些模型需要基于给定的测试实例的演示和输入来生成最终的答案标签。根据广泛使用的设置，分别在5次激发、3次激发、4次激发、0次激发和3次激发设置下评价MMLU、BBH、MATH、HumanEval和MBPP。此外，对于BBH、MATH和MBPP，我们采用了思维链提示技术（Wei et al.，第2022条b款）。

Loss Estimation Models
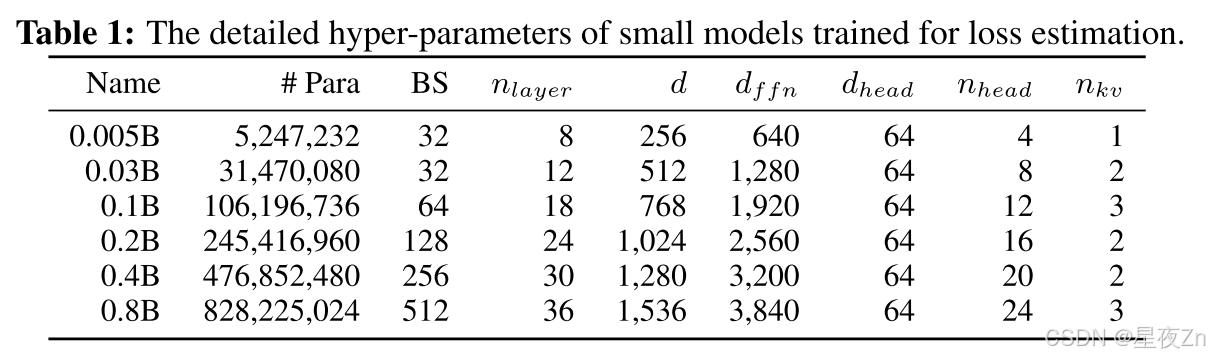
在损失估计步骤中，我们需要使用不同尺度的参数和训练数据运行一系列模型。这些模型将被用作进一步密度计算的参考模型。在这项工作中，我们采用MiniCPM-3- 4 B的训练语料库（Hu et al.，2024），一个广泛使用的边缘大小的模型，以训练小模型。至于模型架构，我们使用分组查询注意力（Ainslie等人，2023），具有SiLU作为激活函数的门控前馈层。我们使用Warmup-Stable-Decay学习率调度器来训练模型。为了估计缩放曲线，我们使用{10，15，20，30，40，60} ×N个令牌来训练模型，其中N指的是参数大小。我们在表1中列出了小尺度模型的超参数。

Performance Estimation Models
在性能估计步骤中，我们引入了额外的经过良好训练的模型来拟合损失-性能曲线。具体来说，我们使用一系列经过良好训练的MiniCPM-3模型及其中间训练检查点。它们的参数规模从5亿到数百亿不等。这些模型使用与我们的缩放模型相同的词汇表，具有不同的参数大小和训练数据集。

Evaluated Models
此外，为了说明密度随时间的变化，我们选择了自Llama-1发布以来广泛使用的LLM进行评价（Touvron等人，2023 a），因为在美洲驼-1之前发布的大多数开源模型在我们选定的数据集上无法实现有意义的性能。具体地，我们评价了以下模型的密度：Llama系列模型（Touvron等人，2023 a，B; Dubey等人，2024）、猎鹰（Almazrouei等人，2023）、MPT（Team，2023）、Phi系列模型（Gunasekar等人，2023年; Li等人，2023年; Abdin等人，2024），西北风（Jiang等人，2023），稳定LM（Bellagente等人，2024），TinyLlama（张等人，2024）和MiniCPM系列模型（Hu等人，2024年）的报告。我们优先使用每个模型的技术报告中报告的结果进行密度计算。此外，我们只评估未经指令调整的基础预训练模型的密度，因为指令调整数据集可能包含类似于我们选择的测试数据的人工注释数据，导致不准确的密度估计。值得注意的是，许多预训练模型还在预训练阶段引入了监督微调数据集，导致测试集污染问题（Wei等人，2023年;多明戈兹-奥尔梅多等人，2024年）的报告。因此，不准确的密度估计仍有待解决，这是我们留给未来的工作。

值得注意的是，我们只评估预训练基础模型的密度，而不进行进一步的监督微调和偏好学习，原因如下：（1）预训练基础模型是模型性能的基础。考虑到进一步比对的影响，例如人类注释的质量和比对算法的选择，引入了与基础模型本身的能力无关的过多混杂因素。(2)LLM与对齐性能的标度律仍然是一个悬而未决的问题，需要进一步探索。如今，有许多方法来提高推理时间期间的性能，例如检索增强生成（刘易斯等人，2020），以及更多地考虑推理缩放定律（OpenAI，2024b）。在这里，我们只考虑基本LLM评估的基本提示技术，因为这种技术不能始终如一地提高该基本模型的性能。对于不同的推理FLOP，我们将密度计算留给未来的工作，这可能会导致推理Densing定律。

3.2 Loss and Performance Estimation Results

我们在图2中给出了两步过程的估计结果。从结果中，我们可以观察到两步估计过程可以有效地拟合不同大小的模型在三个下游任务上的性能。随着测试实例上的损失的减少，性能显著提高，呈S形曲线，并且损失与参数和训练令牌的数量呈幂律关系。

为了评估我们的估计方法的有效性，我们使用参数小于40亿的模型来拟合损失-性能曲线，并保留较大的模型进行预测。图2（B）中的三角形是两个具有数百亿参数的模型。从结果中，我们可以观察到，我们有效地预测下游性能的损失值的基础上。

图2：损失估计和性能估计的结果。这里，线是拟合曲线。（a）中的X轴是指预训练计算，其近似为计算= 6ND。（B）中的三角形是用于预测的较大模型。

3.3 Densing Law

在拟合了损耗比例曲线和性能比例曲线之后，我们进一步测量了自Llama-1发布以来广泛使用的开源模型的密度（Touvron等人，第2023条a款）。我们在图1中展示了每个模型的密度沿着它们的发布日期。从图中我们可以观察到：（1）LLM的密度随时间迅速增加。值得注意的是，2023年2月发布的美洲驼-1的密度低于0.1，而最近发布的Gemma-2- 9 B和MiniCPM-3- 4 B等机型的密度则达到了3.这种密度的增加主要是由于训练前数据规模的增加和数据质量的提高。例如，在1.4万亿个令牌上对Llama-1进行预训练，而Llama-3利用15万亿个令牌并进行仔细的数据清理。(2)更好的性能并不总是导致更好的密度。Llama-3.1- 405 B是目前最先进的开源模型之一，因为它的参数规模很大。然而，它并不是密度最高的型号。这是因为受计算资源和预训练数据规模的限制，我们通常无法完全优化超大型模型的训练设置，从而使它们在成本效益方面不是最优的。

为了进一步说明LLM密度的增长趋势，我们对图1中的包络线进行了线性拟合。具体地说，我们假设最大密度的对数值随时间线性增加。形式上，我们拟合以下线性函数：

$$ln(p_{max})=A\ast t+B$$

式中t为Llama-1发布后的时间间隔（单位：天），ρ为t时刻的最大密度值，A、B为待拟合参数。通过拟合过程，我们得到了A ≈ 0.0073，这意味着大模型的密度大约每ln(2)/A ≈ 95天翻一番。这里，线性回归函数的$R^2$为0.912。

模型密度的增长趋势揭示了当前LLMs发展中的一个重要模式。虽然比例定律表明模型性能随着参数大小的增加而提高，但参数规模的增长受到部署场景中可用的有限计算资源和快速响应需求的限制。因此，大型模型并不只是朝着更大的参数尺寸发展。相反，LLM的开发人员正在努力追求更高的成本效益，旨在以最小的推理成本实现最佳性能。这一发现与摩尔定律在集成电路芯片开发中发现的原理（Moore，1965）一致，摩尔定律强调在有限的芯片面积上增加晶体管密度。因此，我们将我们发现的模型密度的增长趋势命名为稠密定律。

3.4 Corollaries of Densing Law

基于密集定律和我们的评估结果，在这一部分中，我们讨论了几个推论，希望我们的发现能促进LLM的发展。

推理成本呈指数级下降
LLMs的密度呈指数增长趋势，大约每三个月翻一番。这里，密度被定义为有效参数大小与实际参数大小的比率。这意味着，在三个月内，我们可以使用实际参数大小的一半实现与当前模型相当的性能。因此，在达到相同性能的条件下，LLM的实际参数大小也将呈指数下降。实际参数计数的这种减少转化为推断期间的计算成本的降低。因此，LLM密度的指数级增加将直接导致实现相同性能水平的模型的推理成本呈指数级下降。

为了更好地说明LLM推理成本的下降趋势，我们在图3中展示了自GPT-3.5发布以来已实现比GPT-3.5更上级性能的LLM的API定价。从图中可以看出，LLMs的价格呈指数下降。具体来说，在2022年12月，GPT-3.5的价格为100万个代币的20美元，而到2024年8月，Gemini-1.5-Flash的价格仅为0.075美元，减少了266.7倍。粗略地说，LLM的推理成本大约每2.6个月减半。LLM API价格呈指数级下降趋势也见于Schizeller（2024）。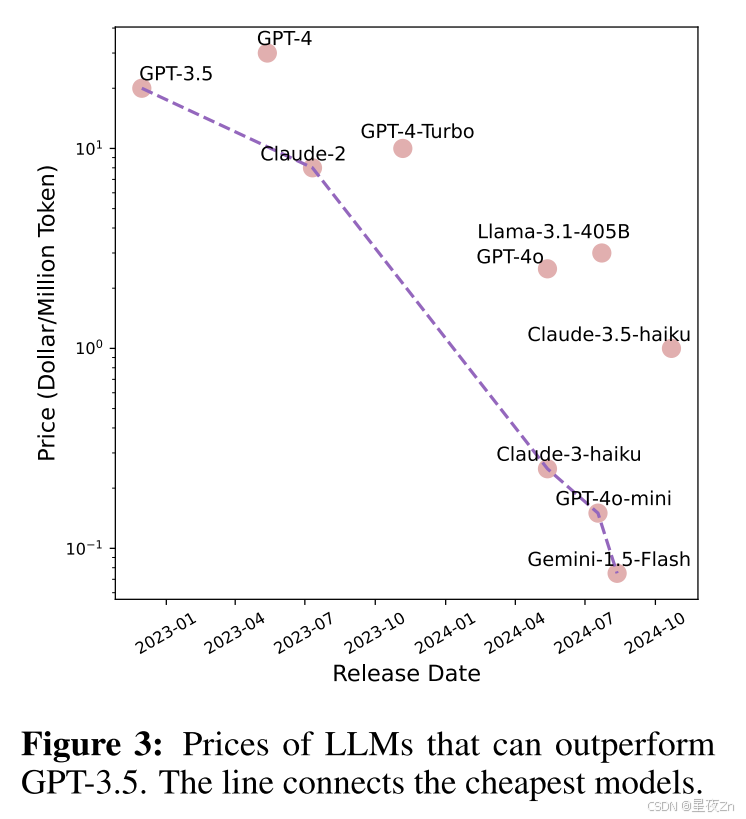

此外，我们还可以观察到，推理成本的下降速度快于LLMs密度的增长速度。这是因为推理成本不仅取决于实际的参数大小，而且在很大程度上取决于推理基础结构。近年来，用于LLM的推理系统已经获得了研究人员的极大关注，包括自注意层的存储器访问速度的优化（Kwon等人，2023年; Dao等人，2022; Dao，2023）和用于前馈网络的稀疏计算优化（Song等人，2023; Liu等人，2023年）的报告。这些进步极大地降低了LLM的推理成本。

密度定律符合摩尔定律
Densing Law描述了模型密度随时间增加的指数趋势，重点是LLM算法级别的改进。另一方面，摩尔定律指出，计算能力呈指数级增长，突出了硬件技术的进步（摩尔，1965年）。这两个原则的结合表明了一个快速接近的未来，高质量的LLM可以在消费级设备（如智能手机和PC）上高效运行，功耗低。算法效率和硬件能力的融合为在日常设备中更容易获得和广泛使用先进的人工智能技术铺平了道路。

具体而言，最近的观察（Hobbhahn等人，2023）发现，相同价格的芯片的计算能力大约每2.1年翻一番。密度定律表明有效参数大小与实际参数大小之间的比率每三个月翻一番。因此，给定固定的芯片价格，可以在其上运行的最大LLM的有效参数大小呈指数增长。这个增长率是模型密度增长率和芯片上晶体管密度增长率的乘积。根据目前的估计，这意味着最大有效参数大小大约每88天翻一番。这种快速增长凸显了算法效率和硬件技术进步的综合影响，表明未来越来越强大的模型可以比以前预期的更快地部署在现有硬件上。

ChatGPT发布后密度增长加速
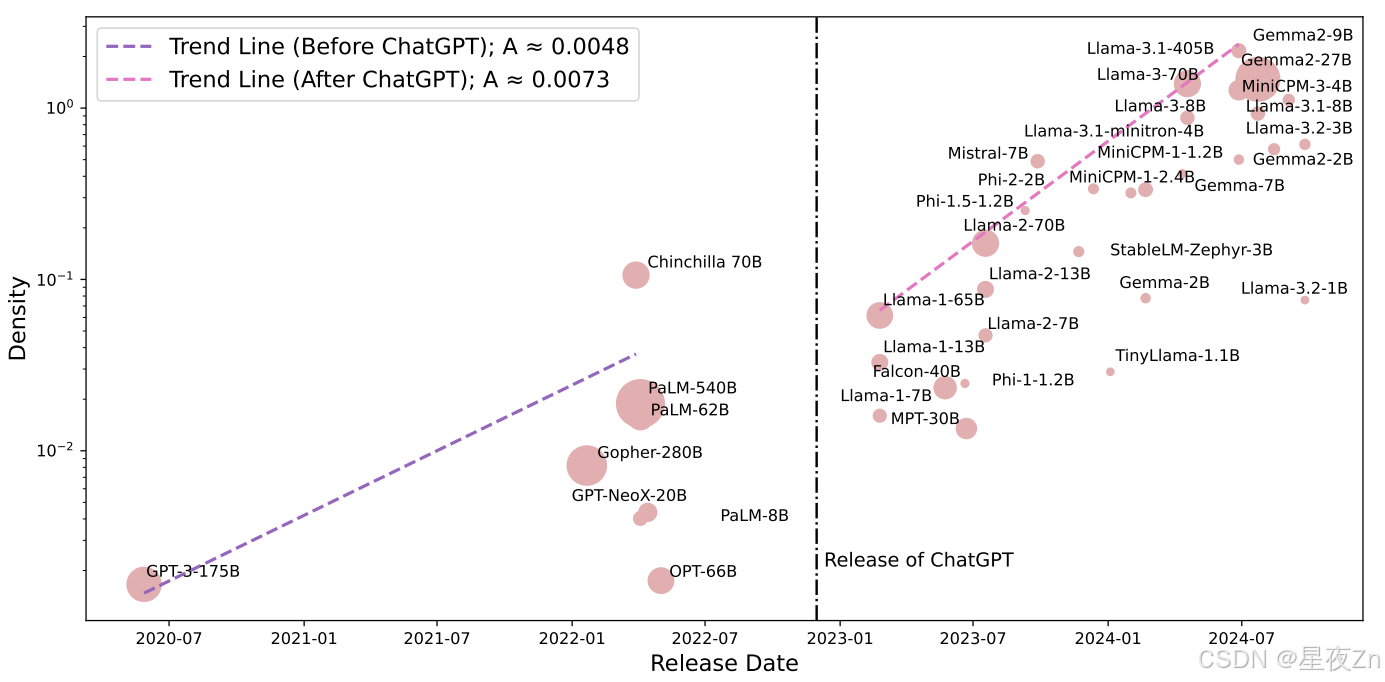
2022年，ChatGPT在各种任务中实现了巨大的性能提升，其零触发泛化能力激发了工业界和学术界为推动LLM的发展做出了重大努力。为了说明ChatGPT发布前后模型密度增长趋势的变化，我们评估了自GPT-3发布以来典型LLM的密度。我们使用MMLU基准来捕获密度的变化。结果如图4所示。

图4：使用MMLU评估的密度。两条趋势线代表ChatGPT发布前后LLM密度的增长。

从图中可以看出，ChatGPT发布后，模型密度的增加速度明显加快。在ChatGPT发布之前，趋势线的斜率约为A ≈ 0.0048，而在发布之后，它增加到A ≈ 0.0073，表明模型密度的增长速度快了50%。几个因素有助于这种加速增长：（1）增加投资：ChatGPT的成功突出了LLM的潜力，导致针对LLM发展的投资显着增加。(2)更多高质量的开源模型：高质量开源模型的兴起降低了LLM的研发门槛。ChatGPT发布后，只有数十亿参数的高质量小型LLM显着增加，其可访问性允许许多研究人员使用相对较小的GPU集群进行LLM研究。因此，我们鼓励社区开源他们的尖端算法和模型，这可以显著提高密度。

Efficient Compression ̸= Density Improvement
LLM通常受到高推理成本的限制，这使得在消费类设备上运行它们具有挑战性。为了解决这个问题，许多开发人员采用修剪和蒸馏技术来压缩LLM。在图5中，我们还展示了几个压缩模型的密度。例如，Llama-3.2-3B/1B和Llama-3.1-minitron 4 B（Muralidharan等人，2024）得自修剪和蒸馏美洲驼-3.1-8B（Dubey等人，2024），而Gemma-2- 9 B/2B是从Gemma-2- 27 B中蒸馏得到的（Team等人，2024年）的报告。结果表明，只有Gemma-2- 9 B模型的密度高于原始模型，而其他压缩模型的密度均低于原始模型。直觉上，剪枝涉及从LLM中移除不重要的神经元，这表明这些神经元可能比其他神经元存储更少的知识。这意味着压缩模型应该直观地实现更高的密度。然而，结果却完全相反。这种差异可能是由于在压缩过程中对较小模型的训练不足，从而使它们无法达到最佳密度。因此，我们鼓励机构群体通过确保在未来的工作中对压缩模型进行充分的培训来应对这一挑战。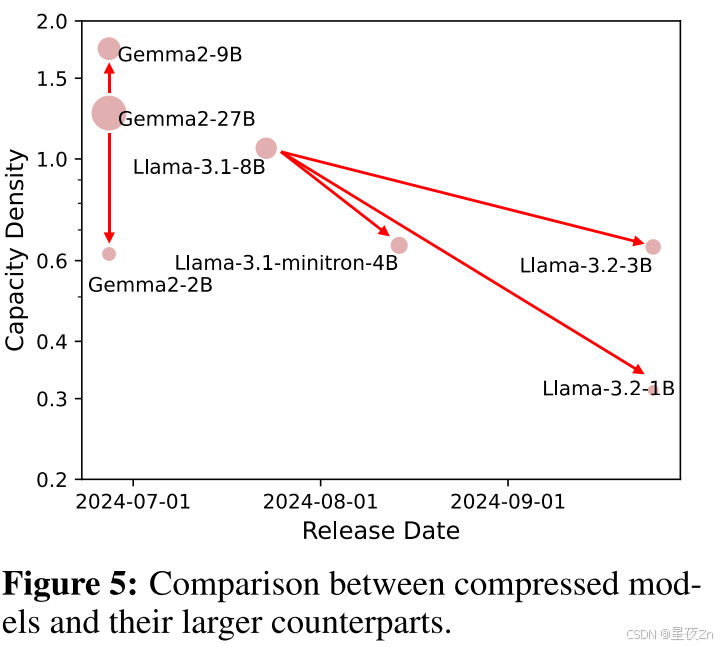

Towards Density-Optimal Training - Green Scaling Law
自从GPT-3的释放（Brown等，2020）和比例律的引入（Kaplan等人，2020），许多研究者专注于训练具有极大参数大小的语言模型，以不断增强模型性能。在这种趋势的指导下，PaLM-540 B（Chowdhery等人，2023）和Gopher 280 B（Rae等人，2021）在各种自然语言处理任务上实现了很大的改进。给定预训练计算资源的约束，最大化预训练群集的使用以开发训练计算最优LLM已成为关键焦点（Hoffmann等人，2022年）的报告。此外，作为主要关注点，推理计算成本已经超过了训练计算成本，导致向使用日益大规模的训练数据来预训练较小模型的转变（Hu等人，2024年; Gunter等人，2024年）的报告。

鉴于密度定律的发现，我们现在鼓励转向密度最佳的LLM预训练。随着全球LLM开发的不断努力，模型密度正在迅速增加，导致每个模型的生命周期缩短。简单地增加LLM的预培训语料库的规模可能会导致更长的开发周期和更高的培训成本。然而，在一个模型发布后不久，预计三个月后将推出一个具有可比性能和更低推理成本的新模型。在这种背景下，LLM开发人员必须考虑模型密度的增长趋势，并采用更有效和更通用的训练技术来提高模型密度。这种方法有助于避免过度的成本投资和与短期利润回收周期相关的损失。

4 Discussion

准确的容量测量
能力密度反映了LLM每单位参数的能力。然而，以目前的技术，我们无法准确评估LLM的绝对能力水平，这意味着量化智能仍然是一个巨大的挑战。因此，在这项工作中，我们设计了一种方法来测量LLM的相对密度值。此外，我们使用广泛使用的基准来评估LLM的性能。然而，基准数量有限和潜在的数据污染问题给业绩评价带来了偏差。因此，在未来推进对LLM能力或智能水平的准确测量将能够更好地计算其密度。

密度律与标度律的联系
LLM的标度律揭示了LLM的性能与其参数和数据大小之间的关系，反映了由大量神经元组成的复杂系统的内在特征。Densing法则进一步凸显了LLM随着时间的推移效率和有效性的发展趋势，标志着人类追求高水平AI模型的技术进步趋势。形式上，在足够的训练数据条件下，标度律将模型损失与参数大小之间的关系解释为：$L=A{N}_{-\alpha }$，这适用于所有基于Transformer的模型的训练。此外，Densing定律表明LLM的开发人员可以通过不断改进数据，算法和架构来增加α，从而减少给定参数大小的模型损失。

Period of Validity of Densing Law
稠密定律揭示了LLM算法的快速发展。在本段中，我们将讨论这样一个问题：模型密度的指数增长将持续多久？我们认为，模型密度的快速增长是由在人员和资源方面的大量投资所推动的。LLMs通用智能能力的提高可以为各个行业带来实质性的好处，进一步鼓励对模型研发的投资。鉴于有限责任公司的巨大潜力，我们相信，《稠密法》将在相当长的一段时间内保持有效。但是，必须不断更新用于评估模型密度的评估数据集，因为LLM很快就会在现有数据集上实现令人满意的性能。在实现人工一般智能的情况下，LLM本身可能能够自主进行科学研究，探索进一步提高密度的新途径。在这一点上，增长的LLM密度可以加快甚至更多，由模型的创新和优化自己的开发过程的能力驱动。

5 Limitations and Future Directions

在本节中，我们讨论了我们提出的方法来评估LLM的容量密度的局限性和未来的发展方向。

公正和全面的评价
LLM的容量密度测量依赖于现有基准来评估模型性能。因此，基准质量对密度测量结果有很大影响。在这项工作中，我们使用那些被研究人员广泛采用的基准来评估各种LLMs。然而，仍然存在以下几个挑战：（1）综合评估：随着LLMs的发展，LLMs的能力显著扩展，例如处理复杂推理任务的能力（OpenAI，2024b）。因此，容量密度测量需要通过纳入反映不断发展的能力的更全面的评估数据集来不断更新。(2)公正评价：随着预训练数据规模的不断扩大和合成数据的构建，一些LLM朝着基准过度优化，导致分数膨胀。为了解决这一问题，我们计划使用新构建的数据集来评估模型性能，从而降低过拟合风险并确保准确的密度估计。

多模态密度
在这项工作中，我们专注于测量语言模型的容量密度。然而，随着多模态应用的增加，测量大型多模态模型的密度和趋势也至关重要。今后，设计合理的多模态模型密度评价方法将是一个重要的研究方向。

Inference Densing Law
最近的研究强调，更多的推理计算成本使LLM能够进行更深入的推理，有效地提高了他们在复杂任务上的性能（OpenAI，2024b）。在这项工作中，我们使用参数大小作为评估模型容量密度的基础。然而，随着思想链推理的重要性不断增长，密度评估应该转向基于推理FLOP。具体地，容量密度可以被形式化为有效推理FLOP与实际推理FLOP的比率。通过这种方式，我们希望LLM以最少的推理步骤获得最佳结果。

6 Conclusion

为了说明最近的趋势，以有效的LLM和定量测量的LLM的训练质量，本文介绍了一种方法来评估LLM的容量密度。通过测量2023年以来发布的开源基础LLM的容量密度，我们展示了一个经验规律：LLM的容量密度随时间呈指数级增长。对一些广泛使用的LLM基准测试的评估结果表明，LLM的密度每三个月翻一番。这意味着，在三个月内，只有一半参数的模型可以实现与当前最先进模型相当的性能。这一发现突出了LLM的快速发展和效率提高。我们讨论了基于该定律的几个推论，并希望该定律及其推论将鼓励LLM社区继续提高模型容量密度，并以最小的计算成本实现最佳性能。

以上内容全部使用机器翻译，如果存在错误，请在评论区留言。欢迎一起学习交流！

如有侵权，请联系我删除。xingyezn@163.com