记录下FATE实现纵向联邦的原理，以逻辑回归为例，重点关注同态加密的使用。

一、背景

在《FATE横向联邦解析：以基于同态加密的逻辑回归为例》中简单记录了横向LR，本文记录下纵向LR的实现。

二、两方（1 Guest + 1 Host）

纵向联邦时，Guest是拥有label的一方，Host是不含lable的建模方，Guest希望通过联合，扩展数据的特征维度。

设想的模型训练流程示意图如下，其中：
（1）Guest有特征X1、X2以及标签Y，有样本U1、U2、U4；
（2）Host有特征X3、X4、X5、X6，有样本U1、U2、U3；
（3）U1和U2是Guest与Host都有的；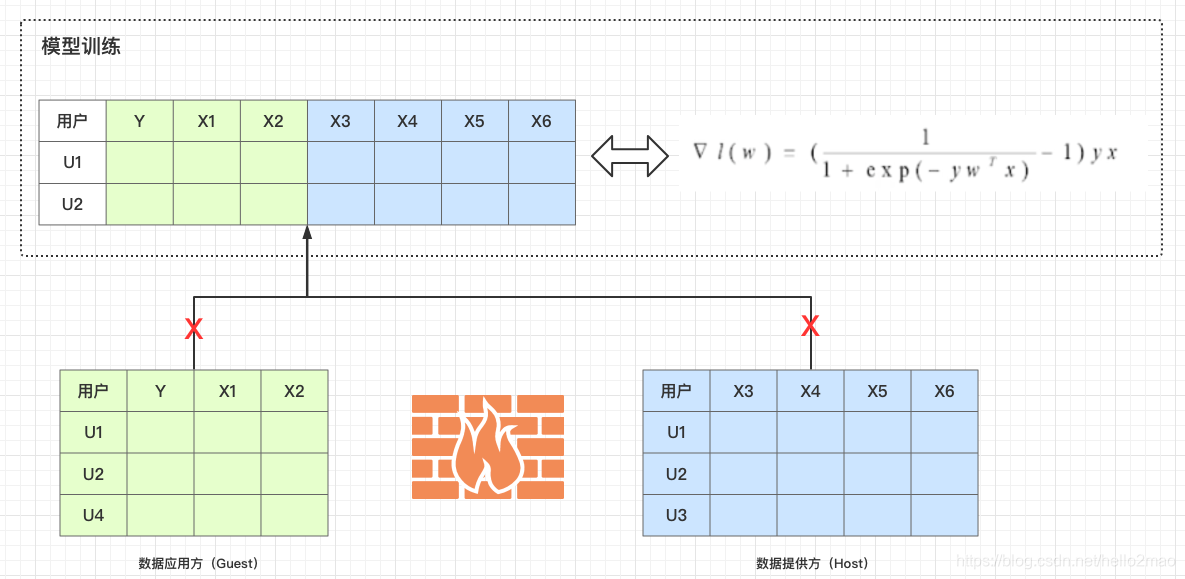

存在的问题：

• 对于纵向联邦，在梯度求解中，x分别在两方，且经过求交，数目是一致的；
• 对于纵向联邦，在梯度求解中，y在Guest方；
• 对于纵向联邦，在梯度求解中，w分别在两方；

所以，下面的流程，就是在不合并两方数据（数据不出域）的前提下，安全、隐私的求出梯度。

与横向一致，对损失函数和梯度做泰勒展开，进行多项式近似，从而支持同态加密（只有数乘和加减法）：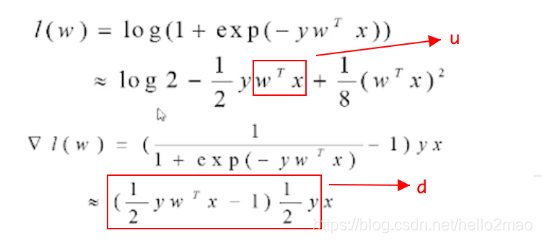

其中：

• u = wx；u称之为forward，分为guest_forward 和 host_forward；
• d = (1/2*ywx-1)*1/2y = 0.25 * wx - 0.5 * y，其中y=1或者-1；d称之为fore_gradient;

实际安全联邦的整体流程如下图所示：（C为Arbiter，UA蓝为Host，UB橙为Guest）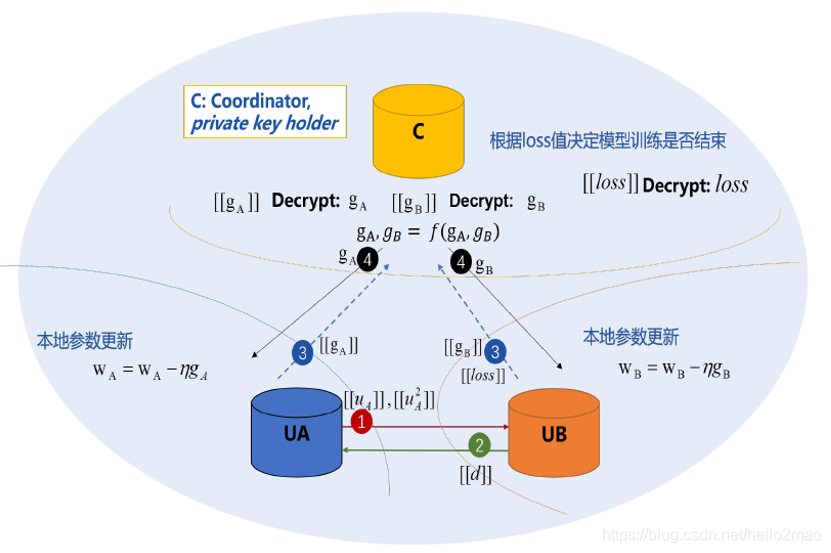

（1）Host（UA）算出它所拥有数据的单边w1 * x，记为ua；并把ua进行同态加密然后发给Guest（UB）；

（2）Guest（UB）根据自己的数据计算单边w2 * x，记为ub；则两方数据总wx=ua+ub；把总wx代入(0.25 * wx - 0.5 * y)即可求得总d；Guest（UB）把d同态机密后返回给Host（UA）；

===>> 至此，Host和Guest都拥有了：求解梯度公式中的d，且d是同态加密的；

（3）Host和Guest分别求出各自的单边梯度∑d*x，即ga和gb，并发给Arbiter；注：ga和gb也是同态加密的；

（4）Arbiter根据获得的ga和gb，使用加密私钥解密后，就可以求得真正的梯度g；然后切分后把相应的部分明文返回给guest和host；guest和host就可以拿着获得的梯度更新本地模型了；

小结：梯度的计算需要数据提供方Host共享同态加密的单边wx给到数据应用方Guest，配合数据应用方Guest的y算出单边梯度，由Arbiter进行聚合才能完成；

三、多方（1 Guest + n*Host, n > 1）

流程类似两方：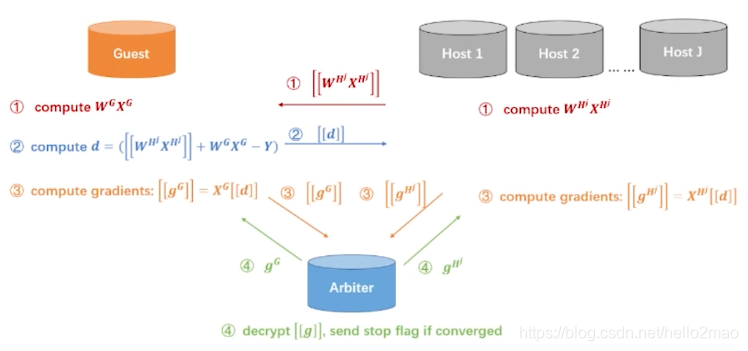

区别：
在两方时，是根据loss值来决定模型训练是否结束的。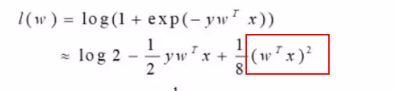

而loss值计算中，wx的平方的值在多方的情况下，会增加计算量以及参与方之间的通行量的增加；

所以，多host的情况下，是根据两轮迭代之间参数的差小于某个值来决定模型训练是否结束的；

附一张更加细节的流程图，省略了fate的一些优化：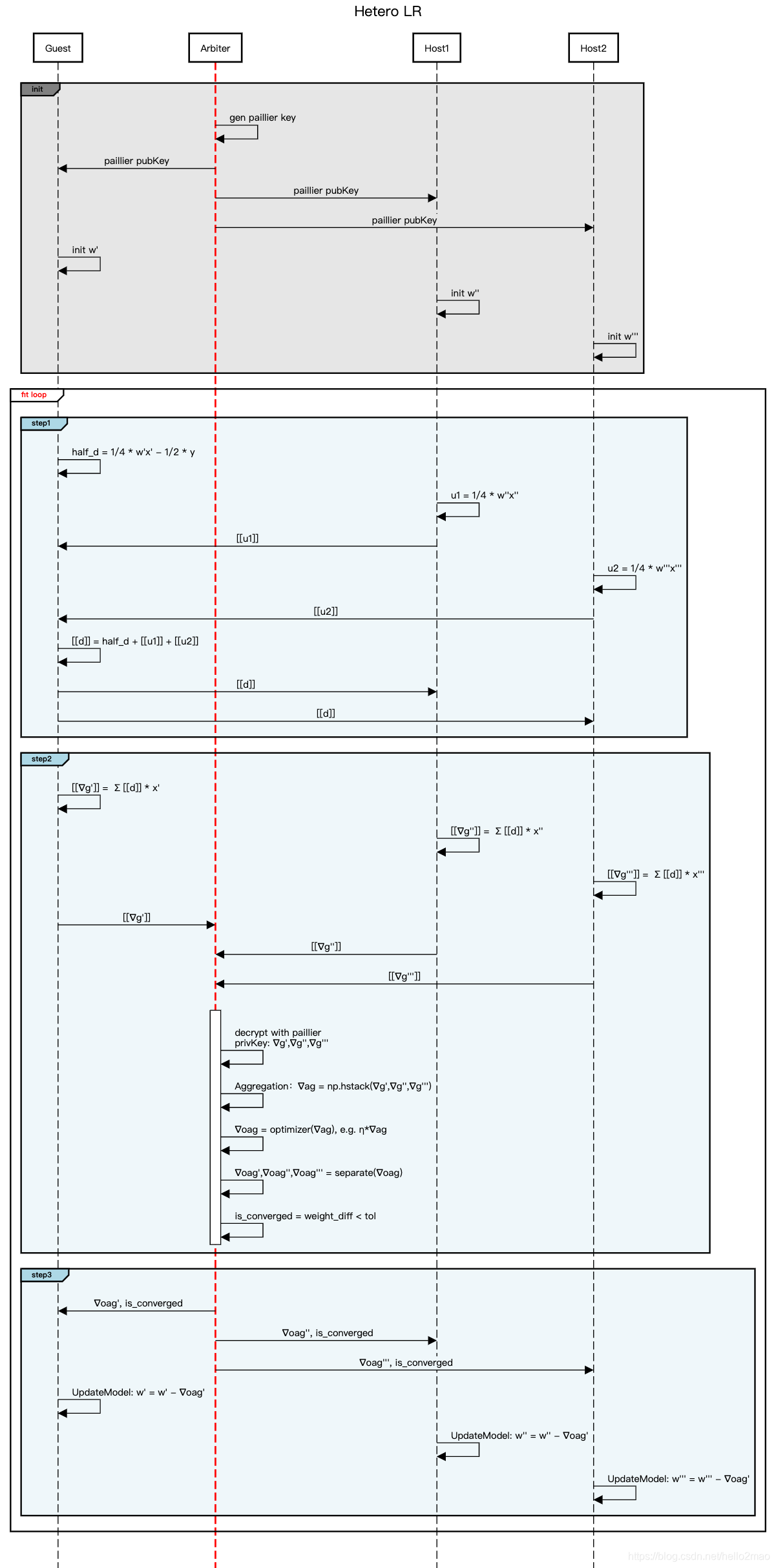

四、同态加密部分

与横向的优化逻辑是一致，
（1）梯度的计算需要多方共享单边wx，配合Guest的y，由Arbiter进行聚合才能完成；
（2）损失loss的计算也是转化为加法同态后，由多方共享的单边wx进行计算获得：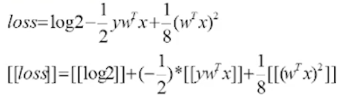

五、总结

【性能折中】同态加密可以协助联邦学习达到数据不出域而实现联合训练的目的，但计算和通讯成本大大增加；
【算法优化】不同的机器学习算法、不同的联邦学习模式（横向、纵向），使用同态的方式会有所差别，且算法需要做定制化优化；
【联合预测】每个参与方只会拥有与自己特征相关的模型参数*；对于横向联邦，数据应用方（Guest）能拿到完整模型，所以可以单独完成预测；但对于纵向联邦，数据应用方（Guest）只能拿到部分模型，所以需要与数据提供方（Host）一起联合预测；