1. PCA作用及原理

主成分分析法主要解决的是将数据降维，并去除数据集的噪音对模型准确性的影响，并同时保持数据集中的对方差贡献最大的特征。比如一个数据集X如下所示，具有m行个样本，每个样本有n个维度的特征。如果维度太多会影响模型运行效率并含有较多噪声影响模型训练精度，我们就可以使用PCA主成分分析法对数据集进行降维。

PCA主成分分析法本质是从一个坐标系转换为另一个正交坐标系，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

新的线性不相关的变量对方差的贡献度不同，通过筛选topn贡献值的特征值从而实现数据的降维。值得注意的是，要对数据进行降维，不得不舍去数据的一些特征信息，通过主从分析的作用就是在保证舍去数据集的特征信息最小的情况下，最大限度的减少数据集的特征维度。如果减少的特征信息中包含了噪音，那么反而会因见少数据维度而提高了精度。

2. python代码实现

本文以sklearn.datasets库中的人脸识别数据为例，进行PCA处理，值得注意的是，笔者在文中代码使用了scikit-learn的版本为1.1.0，此人脸识别数据集mnist共计70000个样本数据，每条样本数据有 784个维度特征。

2.1获取数据集

# -*- coding: UTF-8 -*-
import time
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
# 1. 获取数据集
mnist = fetch_openml('mnist_784')
data = mnist.data
target = mnist.target
print(mnist.data.shape)

2.2 对数据进行PCA运算

# 2.对数据集进行主成分分析运算
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=666)
pca = PCA()  # 通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量
pca.fit(X_train)
variance_contribution_rate = pca.explained_variance_ratio_
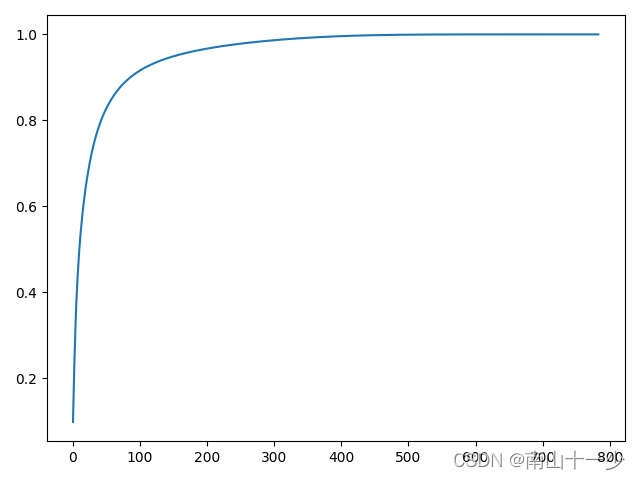
plt.plot([i for i in range(X_train.shape[1])],
         [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()

这里通过正交变换将一组可能存在相关性的原始数据集转换为一组线性不相关的正交数据集，通过曲线图不难看出，其正交数据集对方差的贡献度集中在前100个数据维度中，那么我们就可以通过舍去对方差贡献度较小的特征向量，从而实现降维的目的。往往这些对方差贡献度较少的特征向量中包含了较多的噪声。

2.3 对数据集进行PCA降维后进行KNN算法

# 3. 对数据集进行PCA降维后进行KNN算法
pca = PCA(0.90)  # 保留原数据90%的方差信息，PCA自动计算需要降维到多少维度
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
knn_clf = KNeighborsClassifier()
start02 = time.time()
knn_clf.fit(X_train_reduction, y_train)
score02 = knn_clf.score(X_test_reduction, y_test)
end02 = time.time()
print("PCA数据集的维度为{}".format(X_train_reduction.shape))  # PCA数据集的维度为(56000, 87)
print("PCA数据集测试得分{}".format(score02))  # PCA数据集测试得分0.9747857142857143
print("PCA数据集训练并测试总耗时{}ms".format(int(end02 - start02)))  # PCA数据集训练并测试总耗时6ms

通过以上算法得出结果：

PCA数据集的维度为(56000, 87)
PCA数据集测试得分0.9747857142857143
PCA数据集训练并测试总耗时1ms

笔者在算法中设置保留原始数据90%的方差贡献，PCA提供的方法自动计算出top前87个特征向量，相比之前原始数据784个特征向量来说，计算量大幅降低，特此笔者对原始数据进行同样的算法进行对比，代码如下。

2.4 直接使用数据集进行KNN算法

# 4. 直接使用数据集进行KNN算法
start01 = time.time()
knn_clf.fit(X_train, y_train)
score01 = knn_clf.score(X_test, y_test)
end01 = time.time()
print("原始数据集的维度为{}".format(X_train.shape))
print("使用原始数据集测试得分{}".format(score01))
print("使用原始数据集训练并测试总耗时{}ms".format(int(end01 - start01)))

以上代码运行结果如下：

原始数据集的维度为(56000, 784)
使用原始数据集测试得分0.9716428571428571
使用原始数据集训练并测试总耗时6ms

3. 总结

通过PCA对数据进行预处理，不仅能有效见少数据集特征维度从而提高模型训练和运行效率，而且还能通过去除一部分噪声提高模型精度。