电信保温杯笔记——《统计学习方法（第二版）——李航》第11章条件随机场

电信保温杯笔记——《统计学习方法（第二版）——李航》第11章条件随机场论文介绍概率无向图模型图模型马尔科夫性成对马尔科夫性局部马尔科夫性全局马尔科夫性概率无向图的定义本章概要相关视频相关的笔记相关代码pytorchtensorflowkeraspytorch API:tensorflow API论文电信保温杯笔记——《统计学习方法（第二版）——李航》算法：介绍本文是对原书的精读，会有大量原书的截

电信保温杯

1582人浏览 · 2022-03-11 17:00:04

电信保温杯 · 2022-03-11 17:00:04 发布

电信保温杯笔记——《统计学习方法（第二版）——李航》第11章条件随机场

论文
介绍
概率无向图模型
条件随机场
条件随机场的概率计算
条件随机场的参数估计
本章概要
备注
相关视频
相关的笔记

论文

CRF算法：《Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data》

介绍

电信保温杯笔记——《统计学习方法（第二版）——李航》
本文是对原书的精读，会有大量原书的截图，同时对书上不详尽的地方进行细致解读与改写。

条件随机场（conditional random field）是给定一组输入随机变量 $X$ 条件下另一组输出随机变量 $Y$ 的条件概率分布模型 $P (Y ∣ X)$ ，其特点是假设输出随机变量 $Y$ 构成马尔可夫随机场。

在这里插入图片描述

马尔可夫随机场又称为概率无向图模型。故下面介绍概率无向图模型。

概率无向图模型

首先介绍图模型。

图模型

在这里插入图片描述

具有马尔科夫性的无向图，就是概率无向图，下面介绍马尔科夫性。

马尔科夫性

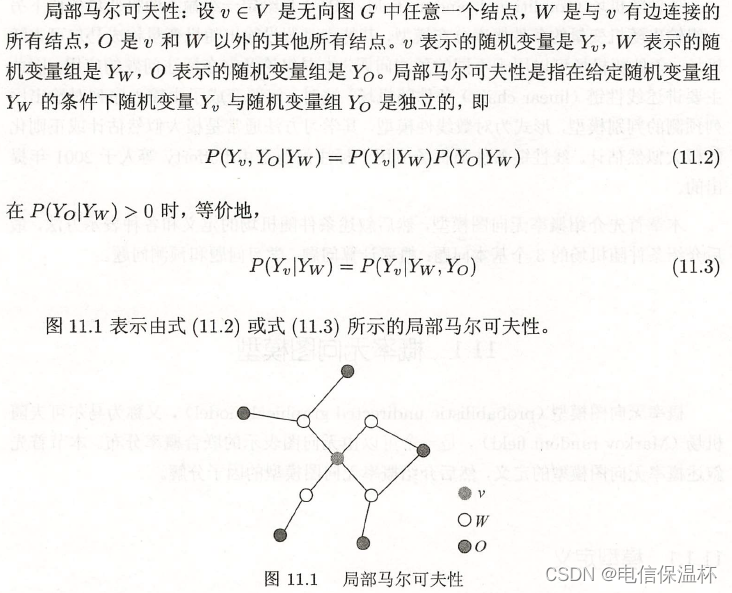
在这里插入图片描述

成对马尔科夫性

在这里插入图片描述

局部马尔科夫性

在这里插入图片描述

全局马尔科夫性

在这里插入图片描述

概率无向图的定义

在这里插入图片描述

概率无向图模型的因子分解

在这里插入图片描述

首先给出无向图中的团与最大团的定义。

团与最大团

定义

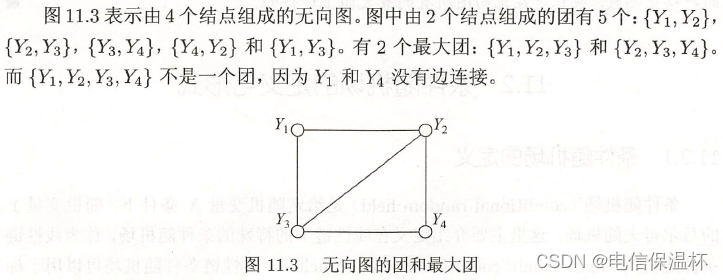
在这里插入图片描述

例子

在这里插入图片描述

因子分解

在这里插入图片描述

总结为如下定理
在这里插入图片描述

了解了马尔可夫随机场后，下面介绍条件随机场。条件随机场（conditional random field）是给定随机变量 $X$ 条件下，随机变量 $Y$ 的马尔可夫随机场。

条件随机场

在这里插入图片描述

条件随机场的定义

在这里插入图片描述

它想说的是， $v$ 点状态的预测，只与跟它连接的节点的状态有关，与跟它没有连接的节点的状态无关，而隐马尔可夫模型的假设 $v$ 点状态的预测只与它的前一个节点的状态有关，这是两者的不同之处。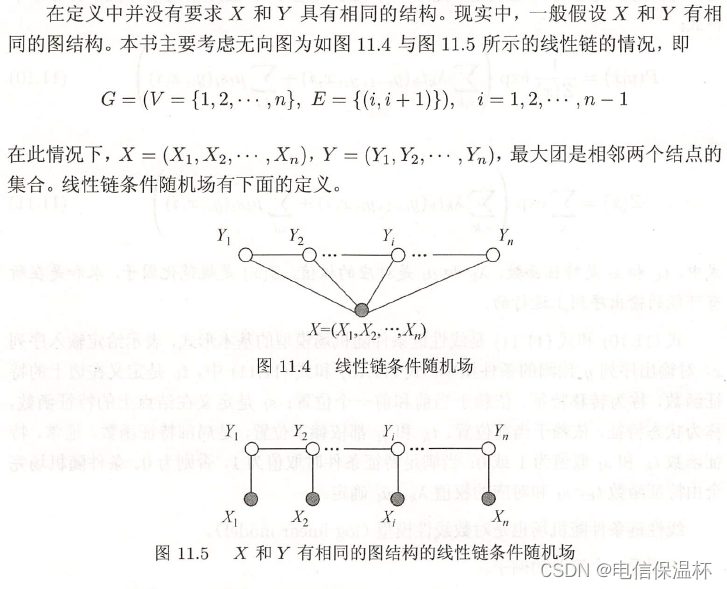
在这里插入图片描述

线性链条件随机场

在这里插入图片描述

它跟条件随机场的定义一致，只不过节点的结构变成了链表，故与条件随机场的定义中的节点 $v$ 相连的节点只有前后2个。

条件随机场的形式

下面是条件随机场 $P (Y ∣ X)$ 公式化的各种表达形式。

参数化形式

就是条件概率写成 $P (Y ∣ X)$ 具体公式。
在这里插入图片描述

其中 $(y_1, y_2, \cdots , y_n)$ 。
在这里插入图片描述

例子

在这里插入图片描述

例子中 $\exp \left[ \sum\limits_{i = 1}^{n+1} \left( \sum\limits_{k = 1}^{5} \lambda_k t_k(y_{i-1} , y_i , x , i ) + \sum\limits_{k = 1}^{4} \mu_k s_k(y_i , x , i ) \right) \right]$ 才与下文矩阵形式书写一致。

简化形式

下面就是把上面公式exp里面的内容进行合并简化。
在这里插入图片描述

矩阵形式

在这里插入图片描述

上式方括号是矩阵元素的表达式，即 $A = [a_{ij}]$ 。
$y_i$ 共有 $m$ 个状态取值， $1,\cdots , n$ ，所以矩阵是 $m$ 阶的。因为 $y_0$ 和 $y_{n+1}$ 只有一种取值，而矩阵 $M_1,M_{n+1}$ 又希望保持矩阵形式，故 $M_1$ 除第一行以外都是0， $M_{n+1}$ 除第一列以外都是0。
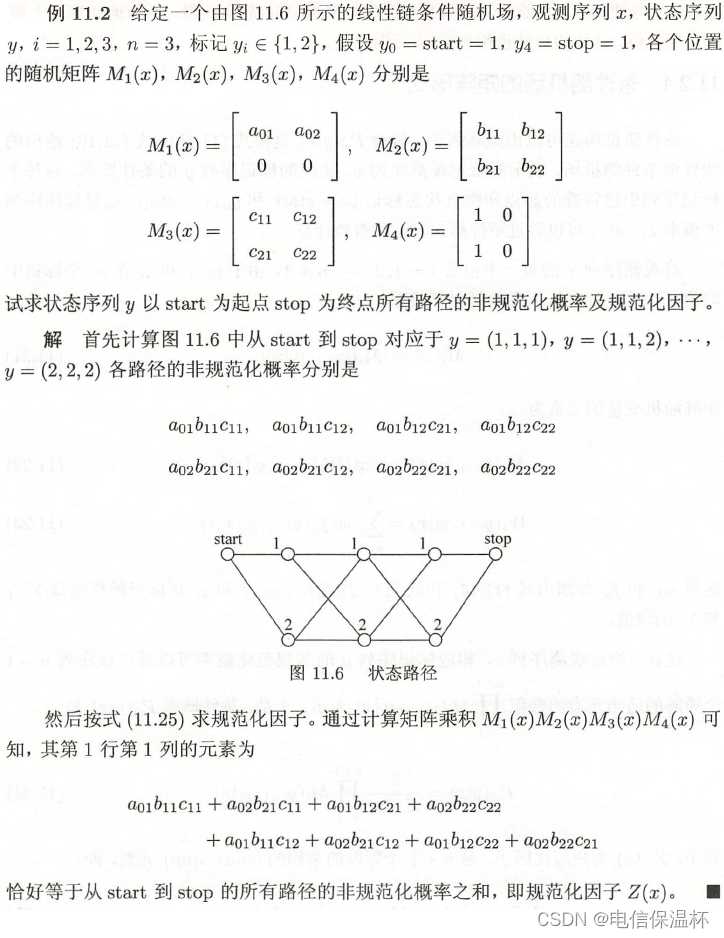
在这里插入图片描述