【推荐系统】基于模型的协同过滤算法

刘润森！

1632人浏览 · 2021-04-16 17:09:52

刘润森！ · 2021-04-16 17:09:52 发布

基于模型的协同过滤算法

本节介绍基于模型的协同过滤算法¹在Top-N推荐中的应用。

核心思想是 通过隐含特征（latent factor）联系用户兴趣和物品 。

思路：对于某个用户，首先得到其兴趣分类，然后从分类中挑选其可能喜欢的物品。

上述基于兴趣分类的方法需要解决3个问题：

如何给物品进行分类？
如何确定用户对哪些类的物品感兴趣，以及感兴趣的程度？
对于一个给定的类，选择哪些属于这个类的物品推荐给用户，以及如何确定这些物品在一个类中的权重？

基础算法

不同于通过编辑给物品进行分类，而是从数据出发， 自动地给物品进行分类， 然后进行个性化推荐。

隐含语义分析技术采取 基于用户行为统计的自动聚类 ，能较好地解决通过编辑进行分类的5种问题：

编辑的意见不能代表各种用户的意见（分类从物品内容出发还是从用户出发）

隐含语义分析技术的分类来自对用户行为的统计，代表了用户对物品分类的看法。隐含语义分析技术和ItemCF在物品分类方面的思想类似， 如果两个物品被很多用户同时喜欢，那么这两个物品就很有可能属于同一个类。
编辑很难控制分类的粒度

隐含语义分析技术允许指定最终有多少个分类，这个数字越大，分类的粒度就会越细，反之分类粒度就越粗。
编辑很难给一个物品多个分类

隐含语义分析技术会计算出物品属于每个类的权重，因此每个物品都不是硬性地被分到某一个类中。
编辑很难给出多维度的分类

隐含语义分析技术给出的每个分类都不是同一个维度的，它是基于用户的共同兴趣计算出来的，如果用户的共同兴趣是某一个维度，那么LFM给出的类也是相同的维度。
编辑很难决定一个物品在某一个分类中的权重

隐含语义分析技术可以通过统计用户行为决定物品在每个类中的权重，如果喜欢某个类的用户都会喜欢某个物品，那么这个物品在这个类中的权重就可能比较高。

隐含语义分析技术有很多著名的模型和方法，其中和该技术相关且耳熟能详的名词有LFM（latent factor model）、pLSA、LDA、隐含类别模型（latent class model）、隐含主题模型（latent topic model）、矩阵分解（matrix factorization）。这些技术和方法在本质上是相通的，其中很多方法都可以用于个性化推荐系统。

下面将以 矩阵分解 介绍隐含语义分析技术在推荐系统中的应用。

矩阵分解（Matrix Factorization, MF）

假设用户——物品数据如下表所示：

	D_1	D_2	D_3	D_4	D_5
U_1	4	3	-	5	-
U_2	5	-	4	4	-
U_3	4	-	5	-	3
U_4	2	3	-	1	-
U_5	-	4	2	-	5

将其转化为用户——物品矩阵 $R_{m \times n}$ ，则：

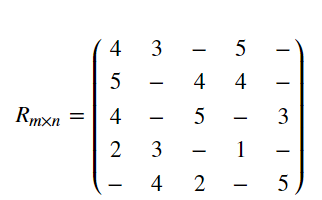
其中“-”表示未打分项。

矩阵分解是指将一个矩阵分解成两个或者多个矩阵的乘积。

对于上面的用户——物品矩阵 $R_{m \times n}$ ，假设将其分解成两个矩阵 $P_{m \times k}$ 和 $Q_{k \times n}$ ，要使得矩阵 $P_{m \times k}$ 和 $Q_{k \times n}$ 的乘积能够还原原始的矩阵 $R_{m \times n}$ ：

$R_{m \times n} \approx P_{m \times k} \times Q_{k \times n} = \hat{R}_{m \times n}$

其中，矩阵 $P_{m \times k}$ 表示的是 $\times k$ 的矩阵，而矩阵 $Q_{k \times n}$ 表示的是 $\times n$ 的矩阵， $k$ 是隐含的参数。

基于矩阵分解的推荐算法

矩阵分解算法属于基于模型的协同过滤算法，后者的步骤主要分为：

建立模型
利用训练好的模型进行推荐

在基于矩阵分解的推荐算法中，上述两个步骤分别为：

对用户物品矩阵进行分解
利用分解后的矩阵预测原始矩阵中的未打分项

通过如下公式计算用户 $i$ 对物品 $j$ 的兴趣：

$r_{ij} = p_{i}^{T}q_{j} = \underset{k=1}{\overset{K}{\sum}} p_{i,k}q_{k,j}$

$P_{i,k}$ 和 $q_{k,j}$ 是模型的参数， $p_{i,k}$ 度量用户 $i$ 的兴趣和第 $k$ 个隐类的关系， $q_{k,j}$ 度量了第 $k$ 个隐类和物品 $j$ 之间的关系。

如何计算这两个参数？

需要一个训练集，对于每个用户 $i$ ，训练集里包含了用户 $i$ 喜欢的物品和不感兴趣的物品，通过学习这个数据集，获得上面的模型参数。

损失函数

为了能够求解矩阵 $P_{m \times k}$ 和 $Q_{k \times n}$ 的每一个元素，可利用原始的评分矩阵 $R_{m \times n}$ 与重新构建的评分矩阵 $\hat{R}_{m \times n}$ 之间的误差的平方作为损失函数，即：

$e^{2}_{i,j} = (r_{i,j} - \hat{r}_{i,j})^{2} = (r_{i,j}-\overset{K}{\underset{k=1}{\sum}}p_{i,k} \cdot q_{k,j})^{2}$
最终，需要求解所有的非“-”项的损失之和的最小值：

$\min loss = \underset{r_{i,j} \neq -}{\sum}{e_{i,j}^{2}}$

损失函数的求解

对于上面平方损失函数的最小值，可以通过梯度下降法求解，梯度下降法核心步骤如下所示：

求解损失函数的 负梯度 ²：

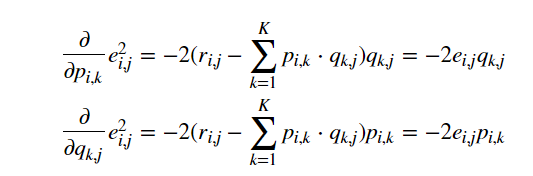
根据负梯度的方向更新变量：

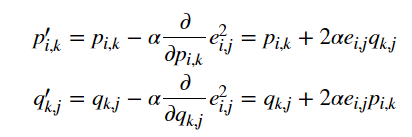
通过迭代，直到算法最终收敛。

加入正则项的损失函数及求解方法

通常在求解的过程中，为了能够有比较好的泛化能力，防止过拟合，会在损失函数中加入正则项，以对参数进行约束。下面是加入 $L_2$ 正则的损失函数：

$e_{i,j}^{2} = (r_{i,j} - \overset{K}{\underset{k=1}{\sum}}p_{i,k} \cdot q_{k,j})^{2} + \frac{\lambda}{2} \overset{K}{\underset{k=1}{\sum}}(p_{i,k}^{2} + q_{k,j}^{2})$

正则化项的 $\lambda$ 可通过实验获得。

利用梯度下降法的求解过程为：

求解损失函数的负梯度：

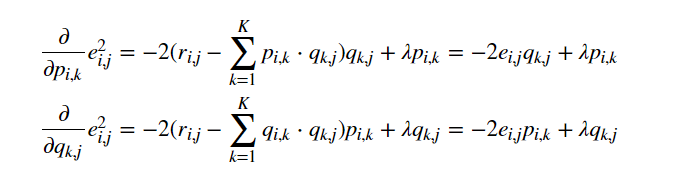
根据负梯度的方向更新变量：

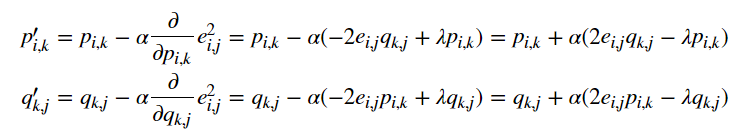
通过迭代，直到算法最终收敛。

其中 $\alpha$ 是学习速率（learning rate），它的选取需要通过反复实验获得。

import numpy as np


def sgd(data_matrix, k, alpha, lam, max_cycles):
    """使用梯度下降法进行矩阵分解。

    Args:
    - data_matrix: mat, 用户物品矩阵
    - k: int, 分解矩阵的参数
    - alpha: float, 学习率
    - lam: float, 正则化参数
    - max_cycles: int, 最大迭代次数

    Returns:
    p,q: mat, 分解后的矩阵
    """
    m, n = np.shape(data_matrix)
    # initiate p & q
    p = np.mat(np.random.random((m, k)))
    q = np.mat(np.random.random((k, n)))

    # start training
    for step in range(max_cycles):
        for i in range(m):
            for j in range(n):
                if data_matrix[i, j] > 0:
                    error = data_matrix[i, j]
                    for r in range(k):
                        error = error - p[i, r] * q[r, j]
                    for r in range(k):
                        p[i, r] = p[i, r] + alpha * (2 * error * q[r, j] - lam * p[i, r])
                        q[r, j] = q[r, j] + alpha * (2 * error * p[i, r] - lam * q[r, j])

        loss = 0.0
        for i in range(m):
            for j in range(n):
                if data_matrix[i, j] > 0:
                    error = 0.0
                    for r in range(k):
                        error = error + p[i, r] * q[r, j]
                    # calculate loss function
                    loss = (data_matrix[i, j] - error) * (data_matrix[i, j] - error)
                    for r in range(k):
                        loss = loss + lam * (p[i, r] * p[i, r] + q[r, j] * q[r, j]) / 2

        if loss < 0.001:
            break
        if step % 1000 == 0:
            print("\titer: %d, loss: %f" % (step, loss))
    return p, q

预测

利用上述过程，可得到矩阵 $P_{m \times k}$ 和 $Q_{k \times n}$ ，模型便建立好了。

在基于矩阵分解的推荐算法中需要为指定的用户进行推荐其未打分的项，若要计算用户 $i$ 对商品 $j$ 的打分，则计算方法为：

$\overset{K}{\underset{k=1}{\sum}}p_{i,k}q_{k,j}$
为用户预测的具体实现的程序如下所示：

def prediction(data_matrix, p, q, user):
    """为用户未互动的项打分

    Args:
    - data_matrix: mat, 原始用户物品矩阵
    - p: mat, 分解后的矩阵p
    - q: mat, 分解后的矩阵q
    - user: int, 用户的id

    Returns:
    - predict: list, 推荐列表
    """
    n = np.shape(data_matrix)[1]
    predict = {}
    for j in range(n):
        if data_matrix[user, j] == 0:
            predict[j] = (p[user,] * q[:, j])[0, 0]

    # 按照打分从大到小排序
    return sorted(predict.items(), key=lambda d: d[1], reverse=True)

隐语义模型和基于邻域的方法的比较

LFM是一种基于机器学习的方法，具有比较好的理论基础。这个方法和基于邻域的方法(比如UserCF、ItemCF)相比，各有优缺点。

理论基础

LFM具有比较好的理论基础，它是一种学习方法，通过优化一个设定的指标建立最优的模型。基于邻域的方法更多的是一种基于统计的方法，并没有学习过程。
离线计算的空间复杂度

基于邻域的方法需要维护一张离线的相关表。在离线计算相关表的过程中，如果用户/物品数很多，将会占据很大的内存。假设有 $M$ 个用户和 $N$ 个物品，在计算相关表的过程中，可能会获得一张比较稠密的临时相关表（尽管最终对每个物品只保留 $K$ 个最相关的物品，但在中间计算过程中稠密的相关表是不可避免的），那么假设是用户相关表，则需要 $\times M)$ 的空间，而对于物品相关表，则需要 $\times N)$ 的空间。而LFM在建模过程中，如果是 $F$ 个隐类，那么它需要的存储空间是 $\times (M+N))$ ，这在 $M$ 和 $N$ 很大时可以很好地节省离线计算的内存。
离线计算的时间复杂度

假设有 $M$ 个用户、 $N$ 个物品、 $K$ 条用户对物品的行为记录。那么，UserCF计算用户相关表的时间复杂度是 $\times (\frac{K}{N})^2)$ ，而ItemCF计算物品相关表的时间复杂度是 $\times (\frac{K}{M})^2)$ 。

而对于LFM，如果用 $F$ 个隐类，迭代 $S$ 次，那么它的计算复杂度是 $\times F \times S)$ 。

如果 $\frac{K}{N} > F \times S$ ，则代表UserCF的时间复杂度低于LFM，如果 $\frac{K}{M} > F \times S$ ，则说明ItemCF的时间复杂度低于LFM。在一般情况下，LFM的时间复杂度要稍微高于UserCF和ItemCF，这主要是因为该算法需要多次迭代。但总体上，这两种算法在时间复杂度上没有质的差别。
在线实时推荐

UserCF和ItemCF在线服务算法需要将相关表缓存在内存中，然后可以在线进行实时的预测。以ItemCF算法为例，一旦用户喜欢了新的物品，就可以通过查询内存中的相关表将和该物品相似的其他物品推荐给用户。因此，一旦用户有了新的行为，而且该行为被实时地记录到后台的数据库系统中，他的推荐列表就会发生变化。

而从LFM的预测公式可以看到，LFM在给用户生成推荐列表时，需要计算用户对所有物品的兴趣权重，然后排名，返回权重最大的 $N$ 个物品。那么，在物品数很多时，这一过程的时间复杂度非常高，可达 $\times N \times F)$ 。因此，LFM不太适合用于物品数非常庞大的系统，如果要用，我们也需要一个比较快的算法给用户先计算一个比较小的候选列表，然后再用LFM重新排名。

另一方面，LFM在生成一个用户推荐列表时速度太慢，因此不能在线实时计算，而需要离线将所有用户的推荐结果事先计算好存储在数据库中。因此，LFM不能进行在线实时推荐，也就是说，当用户有了新的行为后，他的推荐列表不会发生变化。
推荐解释

ItemCF算法支持很好的推荐解释，它可以利用用户的历史行为解释推荐结果。

但LFM无法提供这样的解释，它计算出的隐类虽然在语义上确实代表了一类兴趣和物品，却很难用自然语言描述并生成解释展现给用户。

天启AI社区

GitCode 天启AI是一款由 GitCode 团队打造的智能助手，基于先进的LLM（大语言模型）与多智能体 Agent 技术构建，致力于为用户提供高效、智能、多模态的创作与开发支持。它不仅支持自然语言对话，还具备处理文件、生成 PPT、撰写分析报告、开发 Web 应用等多项能力，真正做到“一句话，让 Al帮你完成复杂任务”。

更多推荐