01 评估指标的局限性

准确率（accuracy）：分类正确的样本占总样本的个数比例
精确率（precision）：分类正确的正样本占分类器判定为正样本的个数比例
召回率（recall）：分类正确的正样本占真正的正样本个数比例
F1 score：精确率和召回率的调和平均值

Q1. 准确率的局限性

当不同类别的样本比例非常不均衡时，占比大的类别往往成为影响准确率的最主要因素。如，当负样本占99%时，模型只需要将所有样本预测为负样本，则可以获得99%的准确率。
为了解决以上问题，可以使用平均准确率（每个类别下的样本准确率的算术平均）作为模型评估的指标。

问题：模型的分类准确率超过95%，但在实际应用中效果差，原因是？
回答：样本类别分布不平衡、评估指标的选择、模型过拟合欠拟合、测试集和训练集划分不合理、线下评估和线上测试的样本分布存在差异……

Q2. 精确率与召回率的权衡

• 搜索排序模型：在一次会话中，用户在交互界面输入需要查询的query，系统给返回其排好序的doc例表的过程。认为模型返回的topN的结果就是模型判定的正样例。
• P-R(Precision-Recall)曲线：横轴是召回率，纵轴是精确率。
  模型对样本进行分类时，都会有置信度，即表示该样本是正样本的概率（即模型通过softmax/sigmoid后得到的分类概率），通过选择合适的阈值，比如50%，对样本进行划分，置信度大于50%的认为是正例，小于50%的认为是负例。
  按照样本置信度从大到小对所有样本进行排序，再逐个样本的确定阈值（阈值=当前样本的置信度），在该样本之前的都属于正例，该样本之后的都属于负例。每一个样本作为划分阈值时，都可以计算当前划分结果的precision和recall，由此画出P-R曲线。P-R曲线深入理解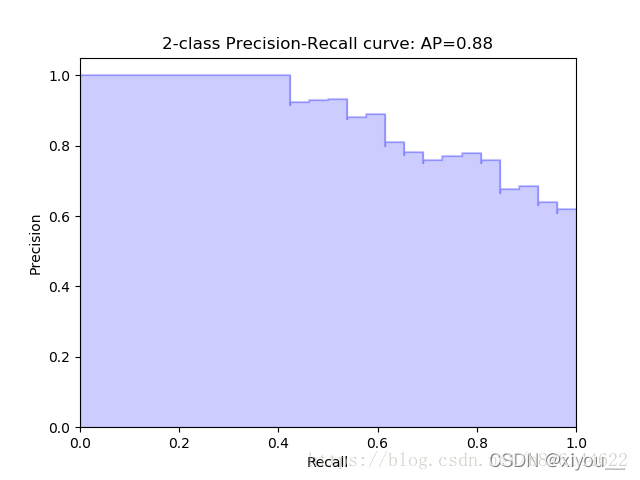
  
  整条P-R曲线是通过将阈值从高到低移动而生成的。原点附近代表当阈值最大时模型的精确率和召回率。
  只用某个点对应的精确率和召回率是不能全面地权衡模型的性能，只能通过P-R曲线的整体表现，才能够对模型进行更为全面的评估。

问题：搜索排序模型返回top5的精确率非常高，但实际使用时无法给用户想要的结果，原因是？
回答：模型的Precision@5（top5的精确率）高，表示模型的返回值的质量很高。模型为了追求高精确率，往往只有在“更有把握”的时候才会把样本判定为正。此时往往会因为过于保守而漏掉很多“没有把握”的正样例，导致召回率低。为了全面评估模型，可使用P-R曲线、F1 score、ROC曲线反应排序模型性能。

Q3. 平方根误差的“意外”

RMSE指标（Root Mean Squard Error，均方根误差）经常被用来衡量回归模型的好坏。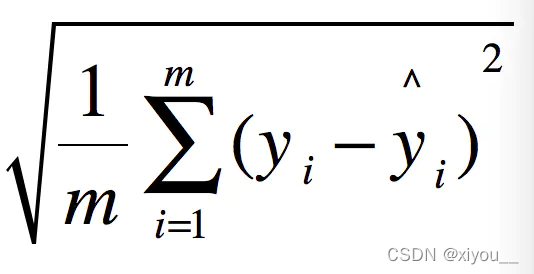

在实际问题中，如果存在个别偏离程度非常大的离群点时，即使离群点数量非常少，也会让RMSE指标变得很差。
针对以上问题，解决方案：

1. 认定离群点为噪声点时，数据预处理阶段过滤噪声点
2. 不认为离群点时噪声点的话，进一步提升模型的预测能力，将离群点产生的机制建模进去
3. 寻找更合适的指标评估模型，如，MAPE（Mean Absolute Percent Error，平均绝对百分比误差），对每一个点的误差进行了归一化，降低了个别离群点带来的绝对误差影响。

问题：回归模型在95%的时间区域内预测误差小于1%，取得了相当不错的预测结果，但是模型的RMSE居高不下，最可能的原因是？
回答：RMSE指标受离群点影响大，如果存在个别偏离程度非常大的离群点，即使离群点个数少，但是也会导致RMSE指标非常差。

05 模型评估的方法

Q1. 在模型评估过程中，有哪些主要的验证方法，他们的优缺点是什么？

• Holdout验证（留出法）
  最简单直接的验证方法：将原始样本集随机划分为训练集和验证集，eg，7：3划分。
  缺点：在验证集上计算出来的最后评估指标与原始分组有很大关系。
• 交叉验证
  k-fold交叉验证：首先将全部样本集划分为$k$个大小相等的样本子集；依次遍历这$k$个子集，每次把当前自己作为验证集，其他$k-1$个子集作为训练集，进行模型的训练和评估；最后将$k$次评估指标的平均值作为最终的评估指标。
  留一验证：每次留下1个样本作为验证集，其他所有样本作为训练集。假设样本总数为$n$，依次对$n$个样例进行遍历，进行$n$次验证，再将评估指标求平均值得到最终的评估指标。留一验证是留p验证的特例。
• 自助法 评估方法（交叉验证 自助法）
  基于自助采样法的检验方法。
  首先对样本综述为$n$的样本集进行$n$次有放回的随机采样，得到大小为$n$的样本集，作为训练集。
  $n$次采样中有的样本被重复抽取，也有的样本没有被抽取，将所有没被抽取的样本作为验证集，进行模型验证。
  目的：样本规模比较小，如何在维持训练集样本规模的前提下进行验证的方法。
  缺点：自助法改变了初始数据集的分布，会引入后计误差

问题：在模型评估过程中，有哪些主要的验证方法，他们的优缺点是什么？
回答：①留出法：直接将样本集按一定比例随机划分为训练集和验证集，缺点是评估结果和分组关系很大，存在随机性；②交叉验证：包含k折交叉验证和留一验证，前者是将样本集划分为k份，依次遍历每份样本，让该样本做验证集，其他所有样本做训练集，k轮后对评估结果取平均。后者是每次只留样本中的一个样例作为验证集，其他所有样例做训练集，该方法时间消耗大；③自助法，用在样本量很少的时候，改变了初始数据集分布，会引入误差。
(咱就是说，k折验证有缺点嘛？？我个人认为深度模型中耗时算一个吧？）

Q2. 在自助法的采样过程中，对n个样本进行n次自主抽取，当n趋于无穷大时，最终会有多少数据从未被选择？

n次采样均未抽中的概率为$(1-1/n{)}^n$
这里涉及极限知识，打字打不出来，当n趋于无限大时，概率约等于$1/e$，即36.8%

问题：在自助法的采样过程中，对n个样本进行n次自主抽取，当n趋于无穷大时，最终会有多少数据从未被选择？
回答：n次采样均未抽中的概率为$(1-1/n{)}^n$，根据极限定理，n趋于无穷大时，$(1-1/n{)}^n$约等于$1/e$，即36.8%。故最终有36.8%的数据从未被选择。

06 超参数调优

Q1. 超参数有哪些调优方法？

超参数搜索算法一般包含三个要素：

1. 目标函数，即算法需要最大化/最小化的目标
2. 搜索范围，一般通过上限和下限来确定
3. 算法的其他参数，例如搜索步长

• 网格搜索：最简单、应用最广泛。通过查找搜索范围内的所有的点确定最优值。然而，这种搜索方案十分耗费计算资源和时间。实际应用中，先使用较广的搜索范围和较大的步长，寻找全局最优质可能的位置；然后逐渐缩小搜索范围和步长，来寻找更精确的最优值。但由于目标函数一般是非凸的，所以很可能错过全局最优值。
• 随机搜索：和网格搜索相似，但是是在搜索范围中随机选取样本点。
• 贝叶斯优化算法：通过对目标函数形状进行学习，找到使目标函数向全局最优值提升的参数。不同于前面两种调优方法，它在尝试下一组超参数时会参考之前的评估结果。具体来说，学习目标函数的方法是，首先根据先验分布，假设一个搜索函数；然后，每次使用新的采样点来测试目标函数时，利用这个信息来更新目标函数的先验分布；最后，算法测试由后验分布给出的全局最佳可能出现的位置的点。需要注意的是，一旦找到一个局部最优点，他会在该区域不断采样，所以容易陷入局部最优值。为了弥补这一缺陷，贝叶斯算法会在探索和利用之间找到一个平衡点（探索：在未采样的区域获取采样点；利用：根据后验分布在最可能出现的全局最佳区域进行采样）
  自动机器学习超参数调整（贝叶斯优化）
  在pytorch上使用ax实现贝叶斯优化算法

问题：超参数有哪些调优方法？
回答：网格搜索、随机搜索、贝叶斯优化算法等。

07 过拟合与欠拟合

Q1. 在模型评估过程中，过拟合和欠拟合具体是指什么现象？

• 过拟合：模型对于训练数据拟合呈过当的情况，即，模型在训练集上的表现很好，但在测试集和新数据上得到表现较差。过拟合会导致模型的泛化能力降低。
• 欠拟合：模型在训练和与测试都表现不好的情况。

问题：在模型评估过程中，过拟合和欠拟合具体是指什么现象？
回答：过拟合是指模型对于训练数据拟合呈过当的情况；欠拟合是指模型在训练和与测试都表现不好的情况。

Q2. 能否说出几种降低过拟合和欠拟合风险的方法？

降低过拟合风险的方法

• 获得更多的数据：对图片平移、旋转、缩放；使用生成式对抗网络合成大量训练数据。
• 降低模型复杂度：神经网络中网络层数、神经元个数
• 正则化方法(正则化如何防止过拟合)：
  L2正则化（权重衰减），即在代价函数后面再加上一个正则化项，是所有参数的平方和
  L1正则化，是所有参数的绝对值和
  正则化通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。
• 集成学习方法：将多个模型集成到一起，降低单个模型的过拟合风险

降低欠拟合风险的方法

• 增加新特征：当特征不足或现有特征与样本标签的相关性不强时，模型容易出现欠拟合。
• 增加模型复杂度
• 减少正则化系数

问题：能否说出几种降低过拟合和欠拟合风险的方法？
回答：略。

待读

• 02 ROC曲线
• 03 余弦距离的应用
• 04 A/B测试的陷阱

补充

贝叶斯算法的基本原理

先验概率：根据以往经验和分析得到的概率，如全概率公式。往往作为"由因求果"问题中的**“因"出现的概率**
后验概率：指在得到"结果"的信息后重新修正的概率，如贝叶斯公式。是"执果寻因"问题中的"果”。
先验分布：是概率分布的一种。与“后验分布”相对。与试验结果无关，或与随机抽样无关，反映在进行统计试验之前根据其他有关参数θ的知识而得到的分布。
后验分布：可看成是在获得样本 x 后对参数先验知识的调整。