写在最前

本文为博主复习高级人工智能这门课程时，针对于归结原理完备性证明这一问题，所做的笔记。这是国科大本门课程的必考题，步骤较为详细，建议理解后记忆。

回顾：归结原理

在命题逻辑中的归结规则是一个单一的有效的推理规则，从两个子句生成它们所蕴含的一个新的子句。归结规则接受包含互补的文字的两个子句 - 子句是文字的析取式，并生成带有除了互补的文字的所有文字的一个新子句。形式上，这里的ai和bj是互补的文字：

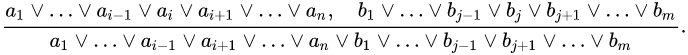
归结规则生成的子句叫做两个输入子句的归结（resolvent）。

当两个子句包含多于一对的互补文字的时候，归结规则可以（独立的）应用到每个这种文字对上。但是，只有要消去（resolve）的文字对可以去除：所有其他文字对仍保留在归结后的子句中。

完备性证明

若证明归结原理，即证明：若KB|=α，则 KB⊢ α，
即证明：若(KB ∧ !α)是不可满足的，则KB⊢ α。

令S={KB, !α}，RC(S)为S使用归结原理得到的所有子句的集合。

下面我们证明：若S不可满足，则RC(S)包含空子句。

即证明其逆否命题：若RC(S)不包含空子句，则S可满足。

我们构造如下指派m：若RC(S)包含一个子句，该子句包含!Ri，且该子句中的其他文字都已被指派为False，则将Ri指派为False，否则将Ri指派为True。

下面证明在m下RC(S)为真。

假设我们对Ri的指派导致RC(S)中首次出现为False的子句，则该子句必然为如下两种形式之一：

1. False ∨ False ∨ False … ∨ Ri
2. False ∨ False ∨ False … ∨ ! Ri

若RC(S)仅包含上面两种形式的其中一种，则我们指派Ri后，必然不会出现False的子句。因此，RC(S)同时包含上述两种形式。

由归结原理，它们归结的子句也应该在RC(S)中，则该子句已经为False，这与“对Ri的指派导致RC(S)中首次出现为False的子句”矛盾。

因此，逆否命题成立，即原命题成立，若S={KB, !α}不可满足，则RC(S)包含空子句。因此，归结原理的完备性得证。