前言

最近在做一个蓝牙定位的小项目，在采集ibeancon蓝牙基站RSSI信号强度数据时，噪声对精度的影响特别的严重，翻阅了些文献，里面提到一种卡尔曼滤波法，所以准备使用卡尔曼滤波法来处理我们收集来的一维rssi数据，这片文章，主要简单介绍了卡尔曼滤波法的原理，还有介绍一下如何用代码来实现卡尔曼滤波法。

一：卡尔曼滤波法原理简单理解

若直接看卡尔曼滤波法的经典五条方差，估计很多人都会懵逼，这都讲了啥，xx是个傻鸟。

这里简单介绍下：

1.卡尔曼滤波法是一种融合了当前的系统估计值（$X_t)$
当前测量值($Z_t$),还有系统估计误差(W_t),测量误差(V_t) ，来对当前进行预测估计的算法进行预测的一个算法。

2.以一个实际温度的例子，介绍下卡尔曼滤波法

（1）要估计k时刻的实际温度值

（2）k-1时刻测量的温度值为$T_{k-1}=23$

（3）假设$T_k=T_{k-1}=25$,$T_k$即为系统估计值

（4）从温度计测量，得到k时刻的测量值为$T_{kz}$

（5）预测的噪声$v(k)=4$，可以是实际环境的温度在一段时间内，温度数据波动的方差

（6）测量的噪声$w(k)=4$，可以是温度计测量的误差

（7）当前有两个$T_k=23$和$T_{kz}=25$,然后引入kalman gain(k_g),通过**预测的噪声$v(k)=4$ ,与测量的噪声$w(k)=4$**的

来融合两个$T_k=23$和$T_{kz}=25$。

${K_g}^2=w(x{)}^2/(w(k{)}^2+v(k{)}^2)$ = $5^2/(5^2+4^2)$

（8)最终计算得$k_g=0.78$，则我们估算出k时刻的实际温度为：

$T=T_k+K_g\ast (T_{kz}-T_k)$ = $23+0.78\ast (25-23)=24.56$

二：卡尔曼滤波法五条经典公式

三：卡尔曼滤波法实现

参考了卡尔曼滤波法C语言实现里边的实现，这里整理了C与python的一维实现。

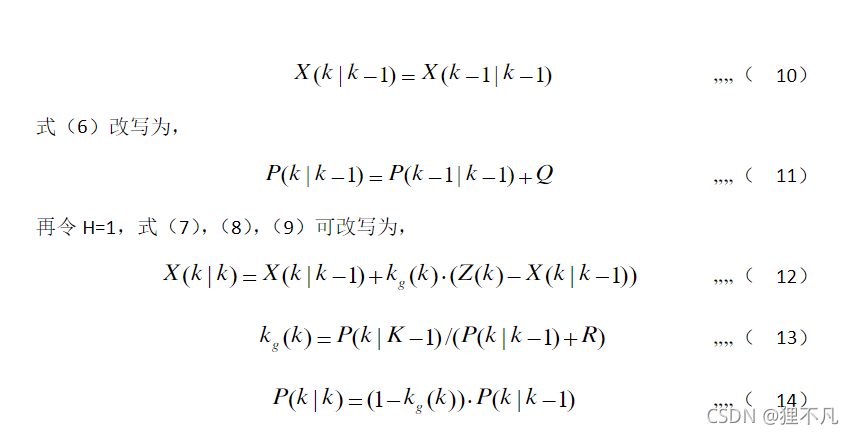
import numpy as np
import matplotlib.pyplot as plt

"""
Q 系统噪声
R 测量噪声
X(k|k-1)   上一次状态预测结果
X(k-1|k-1) 上一时刻的最优预测值
P(k|k-1)   X(k|k-1)对应的convariance协方差
P(k-1|k-1) X(k-1|k-1) 对应的convariance协方差
"""

x_last = 0
p_last = 0
Q = 0.1  #系统噪声
R = 0.5  #测量噪声

def kalman(z_measure,x_last=0,p_last=0,Q=0.018,R=0.0542):
    x_mid = x_last
    p_mid = p_last + Q
    kg = p_mid/(p_mid + R)
    x_now = x_mid + kg*(z_measure - x_mid)
    p_now = (1-kg)*p_mid
    p_last = p_now
    x_last = x_now
    return x_now,p_last,x_last
    
real = np.sin(np.linspace(0,10,100))
chao = np.random.rand(100)-0.5
x = real+chao
y = []
for i in range(len(x)):
    pred,p_last,x_last = kalman(x[i],x_last,p_last,Q,R)
    y.append(pred)
    
plt.plot(real,color="b")  #真实值
plt.plot(x,color="g")     #测量值
plt.plot(y,color="r")     #预测值
plt.show()

参考

【1】卡尔曼滤波法C语言实现
【2】从放弃到精通！卡尔曼滤波从理论到实践~(视频)