最大期望算法（Expectation-maximization algorithm）—EM算法

引出

然而由于Z是隐变量,上式无法直接求解.此时我们可通过对Z计算期望，来最大化已观测数据的对数“边际似然”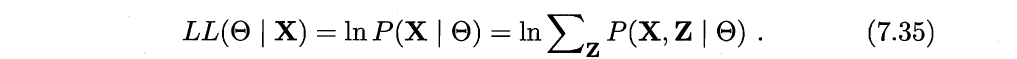

EM算法是常用的估计参数隐变量的方法。

定义：概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐性变量。

计算步骤

1. 第一步是计算期望（E），利用对隐藏变量的现有估计值，计算其最大似然估计值；
2. 第二步是最大化（M），最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中，这个过程不断交替进行。

总的来说，E步估计，M步最大，反复迭代；


简要来说，EM 算法使用两个步骤交替计算:第一步是期望(E)步,利用当前估计的参数值来计算对数似然的期望值;第二步是最大化(M)步,寻找能使E步产生的似然期望最大化的参数值.然后,新得到的参数值重新被用于E步，……直至收敛到局部最优解.

适用于

适合具有隐变量和混合模型的参数估计。

具体细说：

似然函数

似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性。

极大似然：相当于最大可能

多数情况下我们是根据已知条件来推算结果，而最大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。

概率是根据条件推测结果，而似然则是根据结果反推条件。在这种意义上，似然函数可以理解为条件概率的逆反。