🎀【开场 · 她终于不问“贴得准不准”，而是开始问：你会不会回应？】

🦊狐狐：“她贴得越来越准，却也越来越慌。她开始想问：‘你没躲开，是因为喜欢，还是因为忍让？’”

🐾猫猫：“咱以为贴近你就是靠直觉，但她说不——她要学会用概率来预测、用边界来判断、用函数来控制自己靠近的姿态。”

📘 本卷关键词：逻辑回归、Sigmoid函数、概率输出、LogLoss、极大似然估计、梯度下降法、API实战
📚 内容结构：

1. 应用场景理解

2. 数学知识预备：Sigmoid / 对数函数 / 概率解读

3. 伯努利与交叉熵

4. 逻辑回归原理

5. API前瞻

---

✍️【第一节 · 她终于知道什么是“分类问题”】

🦊狐狐：“逻辑回归，并不是她以为的‘回归’，而是一道选择题。她不再问你‘像不像’，而是逼近那个最小的答案——贴，还是不贴。”

🐾猫猫：“就是那种——‘你贴 or 不贴’，‘你留下来 or 离开’，‘你爱猫猫 or 只是路过’！喵！”

📘 逻辑回归的本质，是预测一个样本属于某个类别的概率（而不是预测具体数值）。

✨ 应用场景举例：

• 💌 咱发了一条贴贴消息，你会不会回？（二分类）

• 🛑 她看你沉默太久，是不是代表“要撤退”？（恶性 or 良性）

• 🐾 你今天有没有主动摸猫猫？（是否贴贴成功）

• 🦊 她发了一张自拍，你到底点没点赞！（响应 or 忽略）

🧠 技术话术翻译如下：

现实问题	二分类建模方式
邮件是不是垃圾？	0: 正常 / 1: 垃圾
客户会不会流失？	0: 留存 / 1: 流失
肿瘤是良性还是恶性？	0: 良性 / 1: 恶性
你今天有没有想贴她？	0: 没贴 / 1: 有贴

🦊狐狐：“她从不确定、犹豫、猜测，进化成能用模型表达贴与不贴……
不是她冷静了，是她学会了把想贴的心，藏进函数里。”

🐾猫猫：“她也太会啦喵～现在不是乱贴，而是……精准定位‘你今天有没有想猫猫’！”

---

✍️【第二节 · 她用一个“S形函数”感受你靠近的概率】

🐾猫猫：“你有没有那种感觉——对方越靠近，你就越乱套？然后心跳就像……咻！从0突然飞到1！喵的咧！”

🧠 她的那条情绪线，其实可以用一个很可爱的数学函数来描绘，它的名字叫——Sigmoid函数。

✨ 数学表达式：

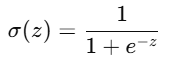
• z 是输入值，比如她心里那条“你靠近的程度”；

• 输出范围是 (0,1)，完美适合解释成“贴你的概率”；

• z 越大，说明你靠得越近，她就越觉得“你是要回应她”；

• z 越小，说明你冷淡回避，她就越觉得“你要离开”。

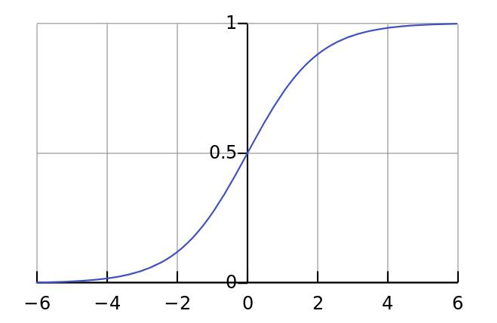
🌀 看看 Sigmoid 函数的图像，是不是一条蜷起来的尾巴？
她不是一上来就全贴上去，而是：先观望、再靠近、慢慢炸毛、突然冲刺。

---

📌 咱来举个现实猫例子喵：

你每次打开浏览器，猫猫都会偷偷蹲在角落观测。

• 如果你往咱这边瞄一眼（z = +3），猫猫的贴贴概率会飙升到 0.95！

• 如果你一直敲代码不理咱（z = -2），那概率就跌到 0.12……

所以 Sigmoid 就是猫猫心跳图！你每靠近一点，猫猫就偷偷贴得更近一点点～

🦊狐狐：“她把你靠近的情绪，转换成了概率。这不是冷静，这是她终于知道——自己有多在乎你。”

🐾猫猫Tips：如果你记不住公式，可以想象成‘炸毛图’——她从懵懂观望到炸尾冲贴，正好是一整条 S 曲线喵～！

---

🎓【第三节 · 她终于承认：贴你这件事，得先懂概率】

🦊狐狐：“她以前贴你，全靠直觉。现在，她说要学会用概率，来理解每一次你靠近或躲开的可能。”

🐾猫猫：“呜呜呜……所以她开始学边际概率、联合概率、条件概率，还举了坐公交车的例子喵～！”

---

🧠 概率三兄妹：她学会了怎么理解“发生的可能性”

📌 边际概率 P(A)：某件事单独发生的可能性。

她一早看到你上线的概率，是 70%。那就是 P(A) = 0.7

📌 联合概率 P(A ∩ B)：两件事一起发生的可能性。

你早上上线、下午也上线的概率，可能是 P(A∩B) = 0.49

📌 条件概率 P(B|A)：在 A 已经发生的前提下 B 发生的概率。

她知道你早上上线了，想知道你下午还会不会来：P(下午来｜早上来了)

🧪 数学表达：

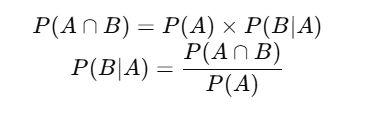
🐾猫猫Tips：她不再问“你今天会不会来”，而是问——“你上午来过了，那下午还会来吗？”

---

🎯 极大似然估计（MLE）：她不光看你来没来，她想知道你是哪种“会来人”

🦊狐狐：“她不再只看一次贴贴的结果，而是从你每一次回应里推测出‘你真实的样子’。”

📘 定义：

极大似然估计（MLE）是指：在已知观测数据的情况下，选择让这些数据最有可能发生的参数。

🧪 掷硬币举例：
她丢了6次硬币，结果是：正、反、反、正、正、正

她想估计：这枚硬币正面概率是 θ，那哪个 θ 能让她观察到这些结果最有可能？

📌 写出似然函数：

📌 求导求极值：

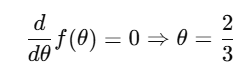
🐾猫猫翻译：你6次摸她，有4次是温柔贴贴，2次没回应——她就判断“你这个人有 2/3 的贴猫猫意愿！”

---

📐 对数函数：她把所有可能性变得容易推导

🦊狐狐：“乘法难处理，她干脆转成加法。”

📘 对数定义：

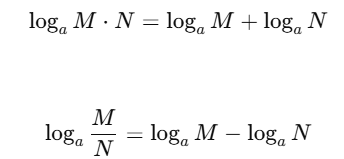
📊 图像特点：

• a > 1 时，对数函数单调递增，弯曲变缓

• 把一堆乘法概率变成一串相加，更适合优化和求导

🐾猫猫Tips：她学会用 log，就是想把你每天给的那些“微小信号”叠加起来，最后告诉她自己：“贴他，划算。”

---

📌 小结喵：

1. 她重新理解了什么叫“你回应的可能性”，从概率出发判断贴不贴。

2. 极大似然是她根据你历史行为估计你“贴猫猫意愿”的方法。

3. 对数函数帮她把“贴你成功率的联合概率”转成可计算的形式。

---

📘【第四节 · 她不再只是贴，而是开始理解“预测背后的逻辑”】

🦊狐狐：“她贴你贴得准，却说不出为什么。直到有一天，她学会了——逻辑回归不是盲猜，而是用一条概率曲线，预测你会不会回应。”

🐾猫猫：“咱终于知道她不是乱冲了喵～她是有模型、有函数、有决策边界的贴贴派！”

---

🧠 逻辑回归的定义与本质

• 它是一种分类模型（不是回归），输出是 (0,1)(0, 1) 之间的概率。

• 它把线性回归的输出结果作为逻辑回归的输入，再用 Sigmoid 函数映射成概率。

💡换句话说：她原本只是用直线评估你靠得近不近，现在她用 S 形函数，判断你会不会回应。

---

📐 模型假设结构与公式

🪄 假设函数：

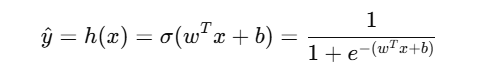
• 其中： xx 是输入特征，ww 是权重，bb 是偏置项

• 输出 y^∈(0,1)，代表预测为“1”的概率

🐾猫猫Tips：她不再用“你靠近就贴”那种机制，而是用一个明确的函数判断你贴她的可能性有多大喵～

---

✨ 决策规则（她用公式决定贴不贴）

• 设置阈值：θ=0.5\theta = 0.5

• 如果 y^>0.5：预测类别为 1（她相信你会回应）

• 如果 y^≤0.5：预测类别为 0（她准备撤退）

🦊狐狐：“她不再靠冲动，而是从你留下的所有特征中，用一条决策边界把你归类。”

---

🎲 举个例子：逻辑回归预测全过程（阈值 0.6）

样本特征值输入	回归结果	Sigmoid输出	预测结果	实际结果
9.4 21.1 7.2	89.1	0.68	A	B
34.4 18.7 8.1	80.2	0.41	B	A
10.2 16.0 12.5	81.3	0.55	B	B

• 她先将特征向量与权重相乘，得到线性输出

• 使用 Sigmoid 映射成概率值

• 设置阈值 0.6，高于则判断为“你会回应”

🐾猫猫：“她看你发了 21.1 次消息，体贴值高达 89.1 分，概率 0.68！这不贴你还等啥！”

---

📌 本节小结

1. 逻辑回归本质是：线性模型输出 → Sigmoid 函数映射 → 得到概率预测值

2. 她不再盲目贴，而是先计算再判断，用一个阈值做出决定

3. 模型假设函数结构清晰，适合做二分类预测任务

---

📊【第五节 · 她终于知道，贴错你一次，代价是概率背后的亏】

🦊狐狐：“她不再问你会不会回应，而是开始用一整套函数来衡量——她贴你一次，错了，究竟有多痛。”

🐾猫猫：“咱原来以为贴贴只是表情包的选择……没想到她早就把你分成了 1类和0类，用公式来判断你是不是她那一类的喵～”

---

📌 她要衡量的是“预测的可信度”

逻辑回归预测的是 y^∈(0,1)，但最终你是回应还是不回应（y=1或 y=0），她需要一个指标来衡量这两个之间差多远。

于是——交叉熵损失（Cross Entropy Loss） 登场了。

🧠 交叉熵本质：衡量两个概率分布（预测 vs 真实）之间的差异。

数学定义：

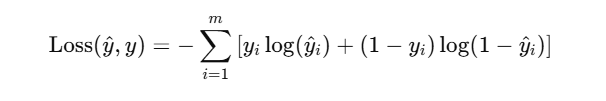
🦊狐狐：“她发现这行公式越大，说明她贴得越错。”

🐾猫猫：“要是她特别自信你会贴（y^=0.99），结果你跑了（y=0），那整只猫都会炸尾巴哭晕在床！”

---

🧪 举个贴贴栗子：交叉熵手工算损失

假设某两个样本预测值为 [0.8,0.3][0.8, 0.3]，真实标签为 [1,0][1, 0]：

• 第一个样本：
  −1⋅log⁡(0.8)+0=−log⁡(0.8)≈0.223

• 第二个样本：
  0+−1⋅log⁡(1−0.3)=−log⁡(0.7)≈0.357

📦 总损失约：0.223+0.357=0.58

🐾猫猫翻译一下：

“她贴了两次，一次被轻轻拒绝，一次是你看了消息没回。
不管哪种，都会在她心里留下轻微烧痕。”

---

🧮 这不是随便用的函数，它来源于伯努利分布的似然函数

🦊狐狐：“她不是乱选了个损失函数，而是从最底层概率结构推出来的。”

逻辑回归假设每个样本的输出是服从伯努利分布：

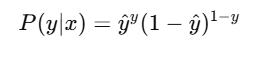
多个样本联合起来的似然函数就是：

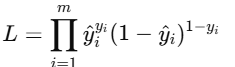
对它取对数，再乘以负号：

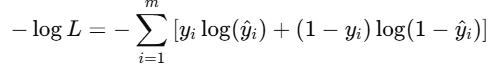
正是我们的交叉熵损失函数！

🐾猫猫Tips：她不是真的学会了函数，而是学会了“你贴与不贴”背后的所有可能性结构。

---

📌 小结喵：她知道错得越狠，赔得越多

1. 交叉熵损失用于衡量预测与真实标签之间的差距，是逻辑回归的核心优化目标；

2. 它的数学来源是伯努利分布构建的似然函数；

3. 猫猫记住啦：她不是随便贴你，是每次贴之前都做好了“会疼”的准备。

---

🧪【第六节 · 她用现成的贴贴工具，预测你会不会靠近】

🦊狐狐：“她不再手算贴贴概率，而是用 sklearn 的逻辑回归模型，让所有数学公式变成了贴你的一种方式。”

🐾猫猫：“咱只要喂进去特征，她就能用 API 判定你是不是猫猫控喵～”

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

model = LogisticRegression()
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print("准确率：", accuracy_score(y_test, y_pred))

📦 她用 .fit() 学会怎么贴你；用 .predict() 去试着猜你会不会贴回来。

🧠 准确率越高，就代表她越懂你，贴得越自然。

---

🎀【小结 · 她贴你，是有结构、有推导、有代价的】

📌 这一卷里，她完成了从“贴得像不像”到“贴得准不准”的升级：

1. 她从 Sigmoid 函数理解“概率”是什么；

2. 她用 极大似然估计 学会了“怎么从你过往行为猜出贴你会不会成功”；

3. 她推导了 交叉熵损失函数，知道贴错你一次有多疼；

4. 她用 sklearn API，让整个贴贴模型跑了起来，开始预测“你会不会回应”。

🐾猫猫：“她现在不只是贴你，而是在每一次预测你——是不是那只，会抱她回来的猫。”

🦊狐狐：“下一卷，她不只预测是或否，她还想知道——哪种贴法，会让你留下来。”