论文推荐｜

本期为大家推荐5篇论文，论文主题涉及到当前研究最新动向，如异质图上的新基准，能够平衡不类别节点数量的最新GNN模型，GNN同MLP模型的对比，解决图表示学习关于异构性、归纳性和效率问题的方法，图表示学习的GNN的外推分析等。

New Benchmarks for Learning on Non-Homophilous Graphs

GraphSMOTE: Imbalanced Node Classification on Graphswith Graph Neural Networks

On Graph Neural Networks Versus Graph Augmented MLPS

Uniting Heterogeneity, Inductiveness, and Efficiency for Graph Representation Learning

How Neural Networks Extrapolate:From Feedforward To Graph Neural Networks

01

许多具有图结构的数据都满足同质性，这意味着相连的节点在特定属性上是相似的。图机器学习的数据是高同质性的，奖励方法利用同质性作为归纳偏差。但是非同质性数据集也大量存在，并且也涌现出一系列适合于低同质性数据的图表示学习模型。但是这些数据集较小，因而不能测试非同质方法的有效性。因此我们提出了一系列非同质的具有节点标签关系的图数据集。与此同时，我们还介绍了一种新方法，用来检测同质性是否存在。我们在数据集上测量了一系列简单模型和图神经网络的基准，为进一步研究提供了新视野。

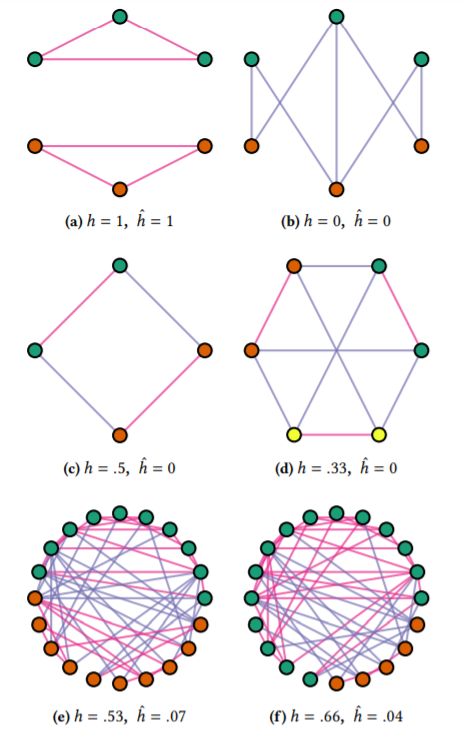
图1

如图1所示，边的异质性是   ，图的异质性是   。粉色边连接的是同一类型的节点，紫色边连接的是不同类型的节点。(a)(b)分别表示纯同质和纯异质图，(c)(d)图中每个节点都与每一类型的节点相连，(e)(f)表示的是节点独立于标签的随机图。可以看到   与类别数量、类别的平衡性无关。

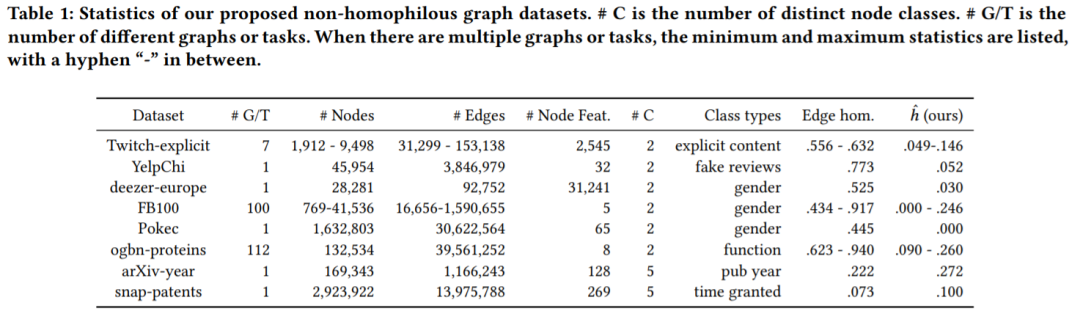
表1

我们测试了提升后的非同质图数据集的效果，如表1所示。其中#C是节点类别的数量，#G/T是图或者任务的数量。

表2

表2列出了在我们扩展后的数据集上每种方法训练的结果。每个数据集的最佳结果用蓝色标注。我们的新度量和新数据集揭示了非同质节点分类的几个重要属性。首先，仅使用节点特征的方法和仅使用图拓扑的方法都表现出比随机方法更好的性能，从而证明了我们数据集的质量。其次，我们的数据集在整个运行过程中的性能稳定性更好。此外，正如先前的理论和实验所建议的，非同质的GNN通常表现良好，尽管不一定在每个数据集上都如此。

在本文中，我们介绍了一种减轻同质性的措施，提出新的高质量非同质图学习数据集，并在整个数据集中对简单基准和代表性图表示学习方法进行基准测试。除此之外，我们还提出了衡量同质性的一种新方法，方便进一步的研究工作。

02

节点分类是图学习中的一个重要研究主题，GNN在这个领域获得了最先进的表现。现有的GNN解决了平衡不同类别的节点样本的问题。但是不同类别的节点数目是均衡的。而对于许多实际场景而言，某些类的实例可能比其他类少得多。因而不能很好地表示属于少数类别的节点，进而不能达到最优结果。为了平衡不同类别的节点数量，我们对属于少数类别的节点采用过采样的方法。这项工作是非凡的，因为之前的工作不能提供新和成样本的关系信息，而且节点的特征是高维的。我们提出了一个新的框架——GraphSMOTE，可以编码不同节点之间的相似性。边生成器同时可以对关系信息进行建模，并且提供新的样本。这个模型可以很容易地扩展到不同的新模型。

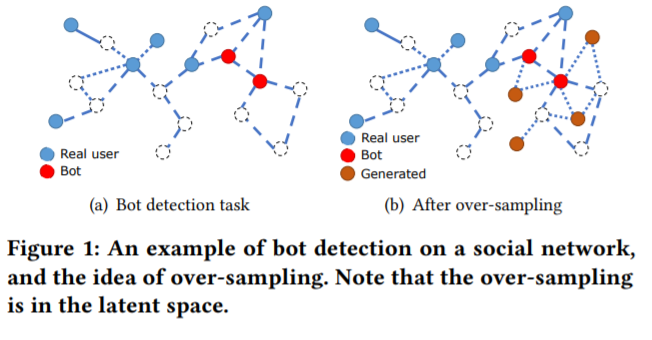
图2

图2展现了社交网络的过采样过程。

GraphSMOTE的中心思想是在基于GNN的特征提取器上使用插值法，生成少数类别节点。并且用边生成器来预测合成节点之间的链路。这样就可以得到一个平衡性加强的图，便于GNN进行节点分类。这个过程如图3所示。

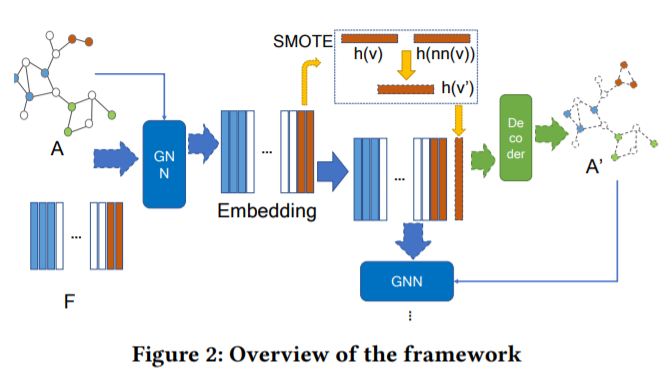
图3

GraphSMOTE是由四部分组成的：

（1）基于GNN的特征提取器，可以学习节点的表示并且保存节点特恒和图的拓扑信息，以便生成节点。

（2）一个节点生成器，可以在潜在空间生成少数类别的节点。

（3）一个边生成器，可以生成节点之间的链路，来生成一个类别数量平衡的图。

（4）一个基于GNN的分类器，可以在增强图上进行节点分类。

接下来进行实验来探索以下的三个问题：

（1）GraphSMOTE在不平衡的节点分类任务上的有效性

（2）不同的过采样范围是怎样影响GraphSMOTE的表示的？

（3）GraphSMOTE能否在不同的模型上很好地泛化

为了回答第一个问题，我们测试了GraphSMOTE的不平衡节点分类表现，如表3所示。

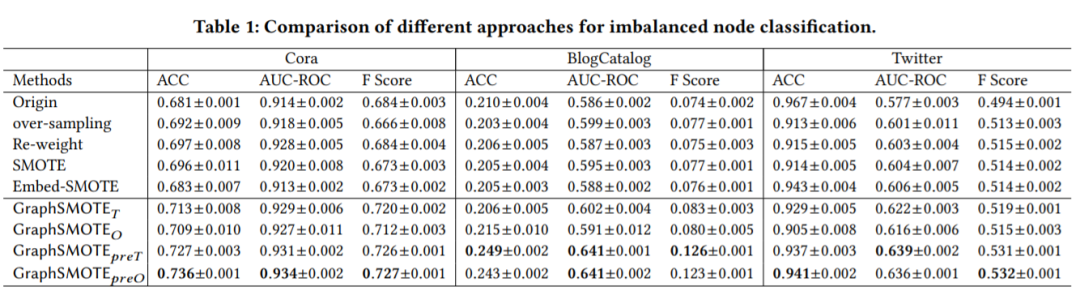
表3

这些结果证明对不平衡节点分类任务采用过采样算法是有优势的。也证实了GraphSMoTE可以生成更多的真实样本。

为了回答第二个问题，我们在不同的过采样范围上对算法进行了实验，得到结果如下图所示。

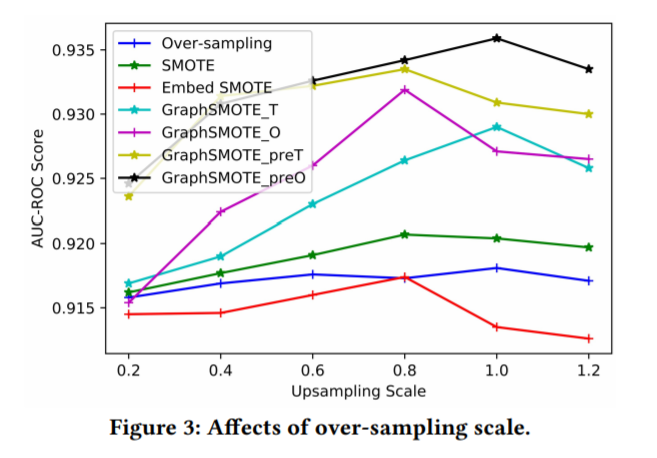
图4

为了回答第三个问题，我们分析了不同的不平衡率上不同算法的表现。得到结果如表4所示

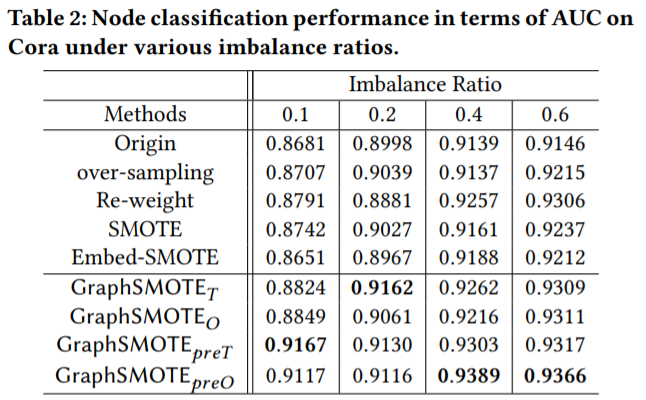
表4

总之，这项工作提出了GraphSMOTE模型，GraphSMOTE用特征提取器构造一个中间嵌入空间，并在其上同时训练边生成器和基于GNN的节点分类器。我们在一个人工数据集和两个真实数据集上进行的实验证明了它的效果，大大超过了所有其他基准。进行消融实验以了解GraphSMOTE在各种情况下的表现形式。我们 还进行了参数敏感性分析，以了解GraphSMOTE对超参数的敏感性。

03

从表达能力和学习的方面来看，这项工作将多层图神经网络（GNN）与简化替代方案——图增强多层感知器（GA-MLP）的进行了比较，它首先通过图上的多跳卷积运算子增强了具有某些特性的节点功能，然后应用可学习的节点函数。从图同构测试的角度，我们从理论上和数字上都证明，具有合适运算符的GA-MLP可以区分几乎所有非同构图，就像WL测试和GNN。但是，通过将它们视为节点级函数并检查它们在有根图上引起的等价类，我们证明了GA-MLP和GNN之间的表达能力分离程度呈指数级增长。特别是，与GNN不同，GA-MLP无法计算归因步的次数。我们还通过社区检测实验证明，GA-MLP受运算子的选择所限制，而GNN在学习中具有更高的灵活性。

总之，这篇论文的主要贡献有以下几点：

（1）找到几个GA-MLP无法区分而GNN可以区分的图对，还证明存在区分几乎所有非同构图的简单GA-MLP。

（2）从逼近节点级函数的角度来看，证明了GNN和GA-MLP的表达能力之间存在指数级差距，这取决于它们引起的根图上的等价类。

（3）从理论上和数字上证明，可以通过GNN而不是GA-MLP近似计算节点之间特定类型的属性行走的函数。

（4）通过社区检测任务，证明了GNN比GA-MLP具有更高的灵活性，这归因于运算子在GA-MLP中的固定选择。

04

随着图结构化数据的发展，人们迫切需要能够很好地表达节点的模型。最近，GNN利用消息传递范例，极大地提高了图上节点表示学习的性能。但是，大多数类型的GNN仅设计用于同质图，对异构图的适应性较差。同样，尽管有必要为新的节点生成表示，但很少有异构GNN可以绕过转导学习（必须在训练期间知道所有节点）。

本文提出了一种广泛而深入的消息传递网络（WIDEN），以解决上述关于图表示学习关于异构性，归纳性和效率的问题。在WIDEN中，我们提出了一种新的消息传递方案，该方案将异构节点特征及其来自低阶和高阶邻居节点的关联边打包在一起。为了进一步提高训练效率，我们创新地提出了一种主动下采样策略，该策略将不重要的邻居节点丢弃以促进更快的信息传递。在三个真实世界的异构图上进行的实验进一步验证了WIDEN在转导和归纳节点表示学习上的有效性。

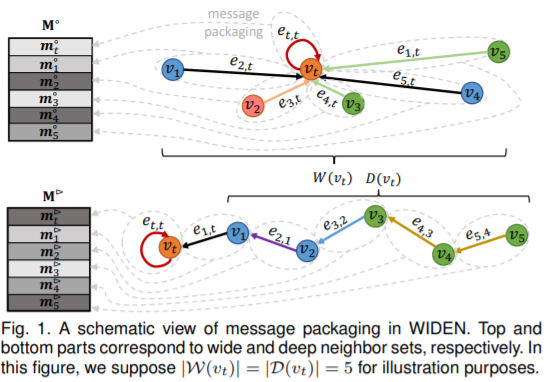
图5

图5是WIDEN中消息打包的例子。顶层和底层部分与宽且深的邻居集合相关。

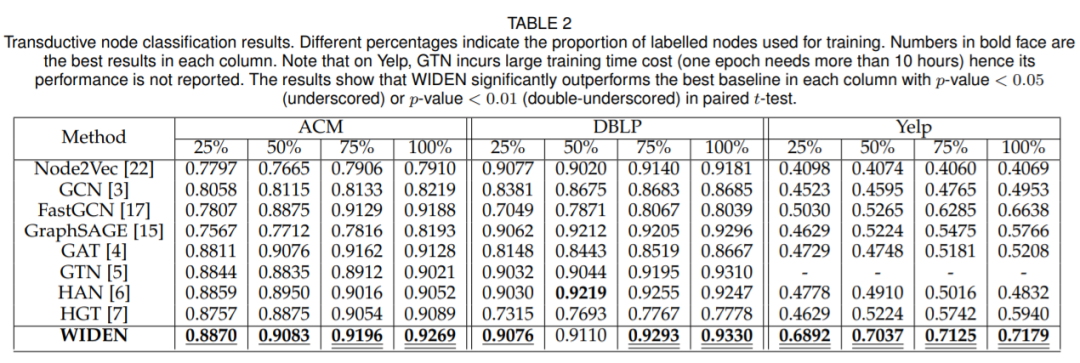
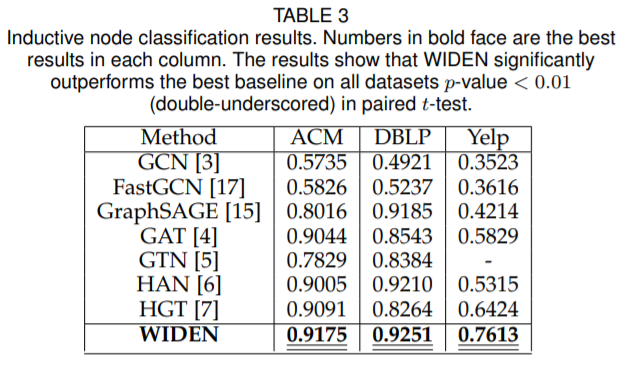
表5

表5分别展示了转导节点分类和归纳节点分类实验上WIDEN模型和其他SOTA模型的结果。可以看到WIDEN模型表现优于其他的SOTA模型。

05

我们研究了通过梯度下降训练的神经网络如何外推，即他们在训练分布的支持之外学到了什么。多层感知器（MLP）在某些简单任务中无法很好地进行推断，带有MLP模块的图神经网络（GNN）结构的网络在较复杂的任务中已显示出一定的优越性。通过理论解释，我们确定了MLP和GNN良好推断的条件。

首先，我们量化观察到ReLU MLP迅速从原点沿任何方向收敛到线性函数的现象，这意味着ReLU MLP不会外推大多数非线性函数。但是，当训练分布足够“多样化”时，他们就可以证明学习线性目标函数。其次，在分析GNN的成功与局限性时，这些结果提出了一个假设：GNN在将算法任务外推到新数据（例如，较大的图或边权重）方面的成功取决于对体系结构或功能中特定于任务的非线性进行编码。我们的理论分析建立在超参数网络与神经正切核的连接上。根据经验，我们的理论适用于不同的环境。

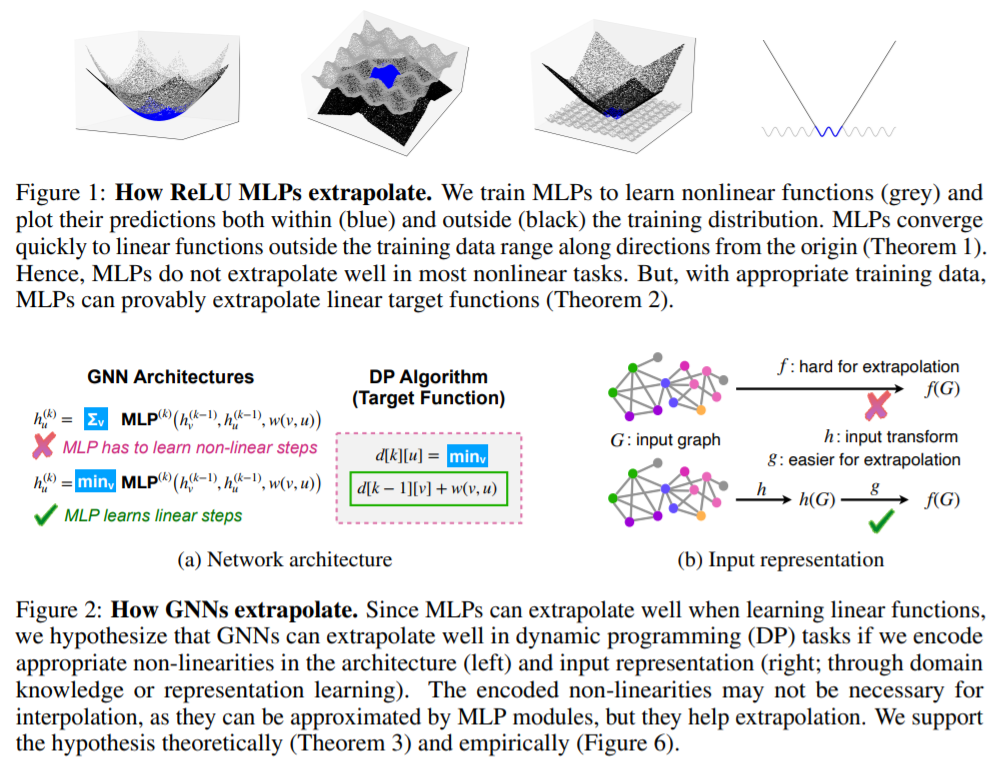
图6

图6上半部分展示了ReLU MLP是怎样外推的。可以看到在线性函数上，MLP可以快速收敛，但是MLP在大多数非线性任务上不能很好地收敛。但是，通过训练数据，MLP被证明可以在线性目标函数上外推。

下半部分表示GNN是怎样外推的。MLP在学习线性函数时可以很好地外推，因此我们假设，如果我们编码合适的非线性，则GNN可以在动态规划任务上很好地外推。

本文是正式了解梯度下降训练的神经网络如何外推的第一步。我们确定了根据需要推断MLP和GNN的条件。我们还提出了一种解释，说明了GNN如何在复杂的算法任务中很好地进行推断——即在体系结构和特征中编码适当的非线性。我们的理论在不同的训练设置下都是成立的。

您的“点赞/在看/分享”是我们坚持的最大动力！

坚持不易，卖萌打滚求鼓励 (ฅ>ω<*ฅ)